第四章. Feasibility of Learning
第四章. Feasibility of Learning
本章主要介绍机器学习的可行性,讨论问题是否可以使用机器学习来解决。
4.1 Learning is Impossible
1.示例描述
1).九宫格样本类型的预测描述:
·图中有6个样本,分成两个类别(+1和-1),通过已知样本来预测新样本的类别?
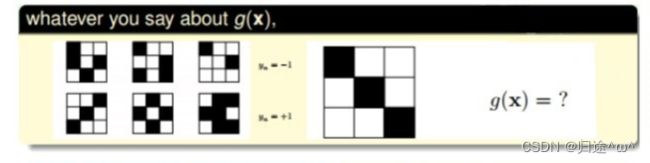
· 新样本类别的预测方法:
①.若根据九宫格的对称性,我们会把它归类为﹢1。
②.若根据九宫格左上角是否为黑色,我们会把它归类为﹣1。
·结论:
根据不同的特性进行分类可以得到不同的分类结果,这些结果貌似都是正确的。
2).数学化二分类示例
·输入特征x是三维数据,训练样本D有5个,测试样本有3个,假设有8个hypothesis,这8个hypothesis在D上,其中5个训练样本的分类是完全正确的(g≈f成立),另外3个测试样本,在不同hypothesis上的表现有好有坏(g≈f不一定成立)。
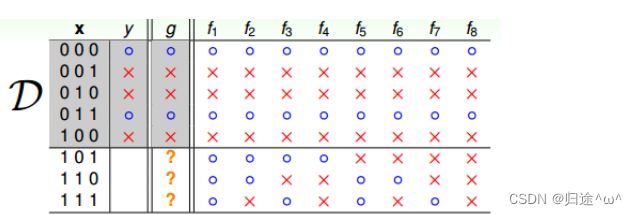
·结论
①.这个例子告诉我们,我们想要在D以外的数据更接近目标函数似乎是做不到的,只能保证对D有很好的分类结果。机器学习的这种特性被称为没有免费午餐(No Free Lunch),简称NFL。
②.NFL定理表明没有一个机器学习算法可以在任何领域总是产生最精准的学习器.
③.不管采用何种学习算法,至少存在一个目标函数,能够使得随机猜测算法是最好的算法,平常所说的一个算法比另一个算法效果更好,只是针对特定条件而言。
4.2 Probability to the Rescue
在4.1中可知:对训练集D以外的样本,机器学习的模型很难对所有测试集都做出正确预判或分类,那是否可以使用一些工具或者方法对未知的目标函数做一些推论,让我们的机器学习模型适用性更加广泛呢?
1.示例
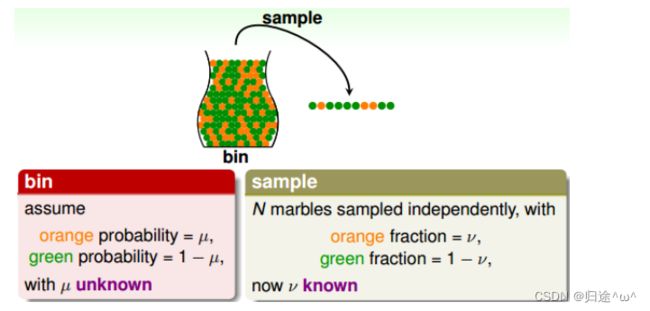
·描述:
如果有一个装有很多橙色球和绿色球的罐子,我们能不能推断橙色球的比例u?
·方法:
根据统计学方法:从罐子中随机取出N个球,作为样本,计算这N个球中橙色球的比例v,那么就可以估计出罐子中橙色球的比例约等于v。
·数学推导:v和u是否接近
1).已知u是罐子里橙色球的比例,v是抽取N个样本中橙色球的比例,当N足够大的时候,v接近于u,这就是Hoeffding’s inequality:![]()
2).Hoeffding不等式说明当N很大的时候,v和u相差不会很大,它们之间的的差值被限定在ε之内,我们把结论v=u称为probably approximately correct(PAC)。

4.3 Connection to Learning
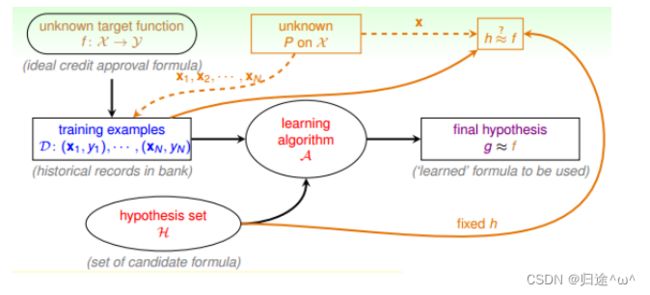
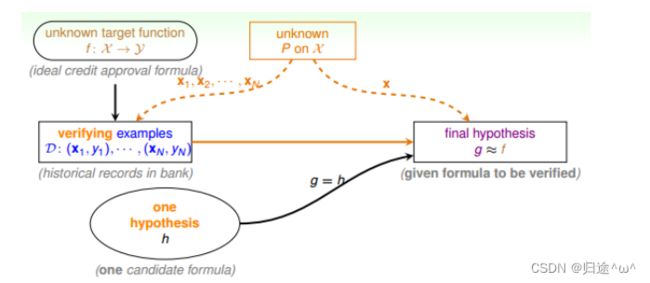
1.示例描述
·如何将罐子的示例对应到机器学习的概念上
1).机器学习中hypothesis与目标函数相等的可能性类比于罐子中橙色球的概率问题;
2).罐子中的每颗小球类比于机器学习样本空间中的x;
3).绿色弹珠类比于h(x)与f相等;橙色弹珠类比于h(x)与f不相等
4).从罐子中抽取的N个小球类比于机器学习中的训练样本D,且这两种抽样的样本与总体样本之间是独立分布的。
·结论:
如果样本N足够大,且是独立分布的,那么从样本中h(x) ≠ g(x)的概率就能推导出在抽样样本外的所有样本中h(x) ≠ g(x)的概率是多少
2.推论
1).将抽样中橙色小球的概率理解为样本数据集D上h(x)错误概率,以此推算出在所有数据上h(x)的错误概率,这是机器学习的工作本质,也是我们可以通过小批量的数据来推测整体数据的原因。
2).这里我们引入两个值Ein(h)和Eout(h)。Ein(h)表示在抽样样本中h(x)与yn不相等的概率;Eout(h)表示在所有样本中h(x)与yn不相等的概率;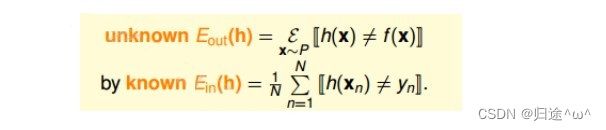
3).Hoeffding’s inequality可以表示为:
![]()
①.该不等式表明:Ein(h)= Eout(h)也是PAC的,如果Ein(h)≈ Eout(h),Ein(h)很小,那么就能推断出 Eout(h)很小,也就是说在该数据分布P下,h与f非常接近,机器学习的模型比较准确。
②.一般地,如果h是固定的,N很大的情况, Ein(h)≈ Eout(h),但并不意味着g≈f。因为h是固定的,不能保证 Ein(h)足够小,即使 Ein(h)≈ Eout(h),也可能使Eout(h)偏大。所以,一般会通过演算法A来选择最好的h,使 Ein(h)足够小,从而保证Eout(h)很小。固定的h,使用新数据进行测试,验证其错误率是多少。
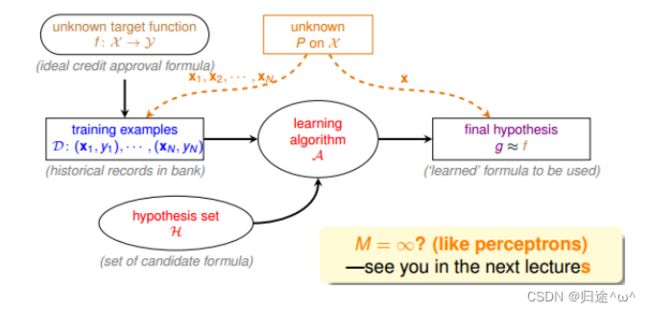
4.4 Connection to Real Learning
1.有多个hypothesis的情况
假设有M个罐子(即有M个hypothesis),若其中某个罐子抽样到的小球全是绿色,那是不是应该选择这个罐子呢?
1).示例描述
假设有150个人抛硬币,那么其中至少有一个人连续抛5次硬币都是正面的概率:
![]()
2).结论
这个概率是很大的,但是也不能说明该硬币单次正面朝上的概率很大,其实都是0.5,一样的道理,抽到全是绿色小球的时候也不能说明这个罐子里都是绿色的球,当罐子数目很多或者抛硬币的人数很多的时候,都会引发这种情况,称为Bad Sample。(Bad Sample就是Ein和Eout 差别很大,即选择过多带来的负面影响,选择过多会恶化不好的情形。)
3).根据许多次抽样得到的不同数据集D,Hoeffding’s inequality保证了大多数的D都是比较好的情况(即对于某个h,保证Ein≈Eout),但是也有可能出现Bad Data,即Ein和Eout差别很大的数据集D,这是小概率时间。
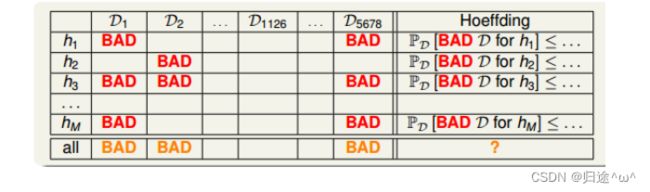
4).也就是说:不同的数据集Dn,对于不同的hypothesis,也可能称为Bad Data,只要Dn在某个hypothesis上是Bad Data,那么Dn就是Bad Data。只有当Dn在所有的hypothesis上都是Good Data,那Dn才不是Bad Data,可以自由选择演算法A进行建模,那么,根据Hoeffding’s inequality,Bad Data的上界可以表示为连级(union bound)的形式:

参数说明:
①.M:hypothesis的个数
②.N:样本D的数量
5).连级(union bound)表明,当M有限,且N足够大的时候,Bad Data出现的概率会很小,既能保证D对于所有的h都有Ein≈Eout,满足PCA,演算法A的选择不受限制,那么满足这种union bound情况,我们就可以和之前一样,选取一个合理的演算法(PLA/pocket),选择使Ein最小的hm作为矩g,一样能保证g≈f,有不错的泛化能力。
6).如果hypothesis的个数M是有限的,N足够大,那么通过演算法A,任意选择一个矩g,都有Ein≈Eout成立;同时,如果找到一个矩g,使Ein≈0,PAC就能保证Eout≈0。至此,就证明了机器学习是可行的。
4.5 总结
本章主要介绍了机器学习的可行性,首先引入了NFL定理,说明机器学习无法找到一个矩g能够完全和目标函数f一样,然后介绍了可以采用一些统计上的假设,例如Hoeffding不等式,建立Ein和Eout的联系,证明对于某个h,当N足够大的时候,Ein和Eout是PAC的。对于h个数很多的情况,只要有h个数M是有限的,且N足够大,就能保证Ein≈Eout,证明机器学习是可行的。