leetcode数组专题
这么鬼使神差的我就点进来啦,于是乎,数据结构的路,给爷冲起来!
虽然是数组专题,但是很多问题都涉及的方面不一样,里面的算法思路也不一样,所以会以不同的算法思路来划分一下
数组
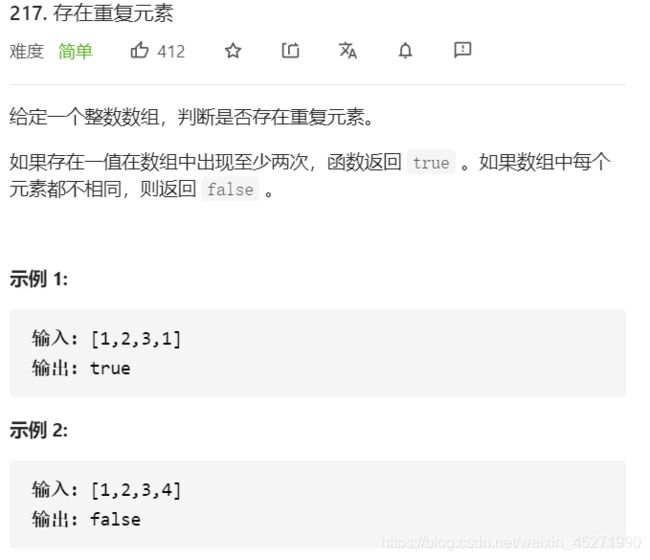
存在重复元素
思路一:哈希表
注意Hashset的构造方法里面只能传Collection
LinkedList<Integer> linkedList = new LinkedList<>();
HashSet<Integer> hashSet = new HashSet<>(linkedList);
class Solution {
public boolean containsDuplicate(int[] nums) {
Set<Integer> set = new HashSet<>();
for(int e : nums){
set.add(e);
}
return ! (set.size() == nums.length);
}
}
思路二:排序后两两比较
class Solution {
public boolean containsDuplicate(int[] nums) {
Arrays.sort(nums);
for(int i = 0; i< nums.length -1;i++){
if(nums[i] == nums[i+1]){
return true;
}
}
return false;
}
}
最大子序和
思路一:动规
状态表示:dp[i] 表示以i结尾的字串的最大值
转移方程:dp[i] 是 上一次的dp[i-1] + nums[i] 和值 和 以当前i 重新开始的新的字符的值 中取max
class Solution {
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
int maxNum = Integer.MIN_VALUE;
for(int i = 0 ;i < nums.length;i++){
if(i == 0) {
dp[i] = nums[i];//初始化
}else{
dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);
}
}
for(int i = 0 ;i < nums.length;i++){
maxNum = Math.max(maxNum,dp[i]);
}
return maxNum;
}
}
优化解法:
class Solution {
public int maxSubArray(int[] nums) {
int length = nums.length;
int max = nums[0];
//now就是用来记录上一个状态的
int now =0;
//状态初始化
for(int i = 0;i < length;i++){
//比较如果从上一个状态转移到这个 和从0 开始进行状态转移
//并且让now记录当前的状态
now = Math.max(now+nums[i],0+nums[i]);
max = Math.max(max,now);
}
return max;
}
}
两数之和
使用hashmap 的做法,把遍历过的值可以保存起来,方便快速检索。这样的做法可以达到遍历一次,并且可以保留遍历过的值!
- key 是遍历到的num[i]
- value 是遍历的index 下标
每次遍历到一个数字的时候,看看可以和当前数字和为target的元素是否遍历过,如果没有九八当前元素的值和index加入进入。
class Solution {
public int[] twoSum(int[] nums, int target) {
int res[] = new int[2];
HashMap<Integer,Integer> map = new HashMap<>();
//键存放的当前的值 值存放的是当前的下标
for(int i = 0; i< nums.length;i++){
int sub = target -nums[i];
if(map.get(sub) == null){ //看看map中是由有和当前的值何为target的
map.put(nums[i],i);
}else{
res[0] = map.get(sub);
res[1] = i;
break;
}
}
return res;
}
}
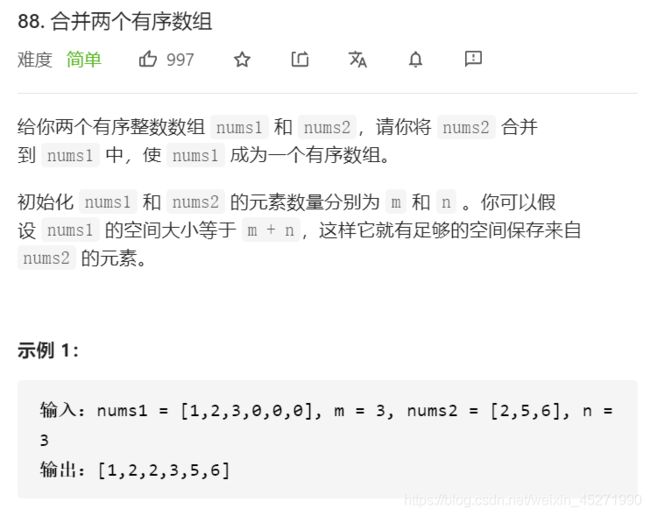
合并两个有序数组
思路一:两个数组拼接在一起,然后排序!
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
for(int i = 0 ; i < n; i++){
nums1[m+i] = nums2[i];
}
Arrays.sort(nums1);
}
}
思路二:新建一个数组大小是两个数组的大小和 m+n
分别遍历两个数组,均指向头部,然后比较大小。将小的加入新建的数组中,然后移动指针再次比较,直到任意一个先结束。然后看看是否有没有遍历完的数组,依次加入即可。
但是上述的思路,需要m+n的空间。
思路三:由于第一个数字长度是 m+n 所以依次比较两个数组
从后往前比较,然后把较大的的放入第一个数字的最后一个位置。
之后再次比较,从后往前对第一个m+n 的数字进行再次排序
这样可以保证两个数组的值不会在没有使用之前就被覆盖
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int cur1 = m-1;
int cur2 = n-1;
int cur = m+n-1;
while(cur1 >= 0 && cur2 >= 0){
if(nums1[cur1] >= nums2[cur2]){
nums1[cur] = nums1[cur1];
cur1--;
}else{
nums1[cur] = nums2[cur2];
cur2--;
}
cur--;
}
while(cur2 >= 0){
nums1[cur] = nums2[cur2];
cur2--;
cur--;
}
}
}
两个数组的交集II(※)
个人觉得这个题难度应该不能写easy!
思路一:使用哈希表
把一个数组里面所有的元素都放入set中去,然后再遍历第二个数组的每个元素,如果存在对应的值+1,最后找到所有大于等于1 的数字即可。
这个思路,好像看起来没有什么毛病,但是一个数组里面一个元素本身就是可以重复出现的,那么,对应的key到底是交集出现的,还是本身数组重复出现的?
首先遍历第一个数组,并在哈希表中记录第一个数组中的每个数字以及对应出现的次数,然后遍历第二个数组,对于第二个数组中的每个数字,如果在哈希表中存在这个数字,则将该数字添加到答案,并减少哈希表中该数字出现的次数。
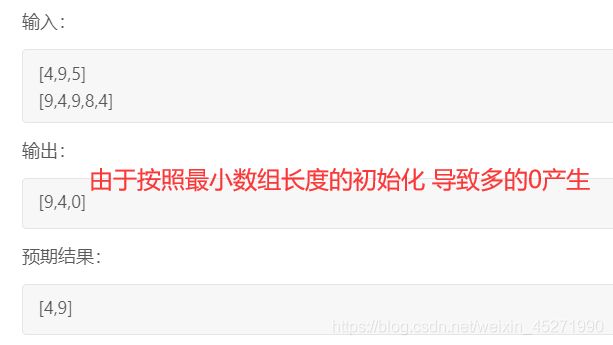
解决按照小数组长度初始化方式就是,这样的写法可以避免写冗余代码!

还有一个坑点 : 结果数组的初始化长度是按照最小的数组长度初始化的,但是如果最后的结果是这样的!
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
HashMap <Integer,Integer> map = new HashMap<>();
if (nums1.length > nums2.length) {
return intersect(nums2, nums1);
}
for(int num : nums1){
map.put(num,map.getOrDefault(num,0)+1);
}
int [] arr = new int[nums1.length];
int i = 0;
for(int num: nums2){
if(map.containsKey(num)){
int val = map.get(num);
if(val > 0){
arr[i++] = num;
map.put(num,val-1);
}
}
}
return Arrays.copyOfRange(arr,0,i);
}
}
但如果还要解决里面遗留的问题,如果当然的数字的val 在-1 之后的值小于0 了那么就从哈希表里面删除即可!
买卖股票的最佳时机(※)
思路一:暴力遍历
如果使用暴力遍历法,找到数组中最大和最小的数字,但是找到的是7 和1 ,但是卖出的价格不能低于买入的价格,所以不可以这么做!
我的思路,双指针,max 和 min 刚开始的index 都指向第一个元素 ,然后遍历,如果出现比当前指向大 或者小的就更新index 。
同时由于当前的最大的index 的下标是不可以在最小的index 之前的,所以一旦出现这样的情况,就让最大和最小的都指向当前遍历到的元素,但是这样的思路是错的!
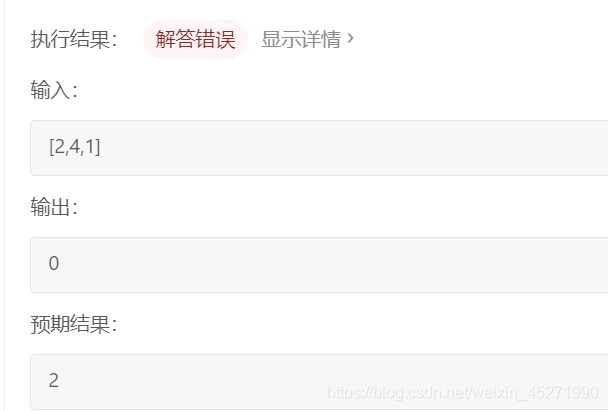

当我看了一眼题解发现我确实是个傻子!为啥这么简单的暴力我都写不出来????
class Solution {
public int maxProfit(int[] prices) {
int max = 0;
for(int i = 0; i< prices.length;i++){
for(int j = i+1; j < prices.length;j++){
int sub = prices[j]-prices[i];
if(sub > max){
max = sub;
}
}
}
return max;
}
}
行吧,好不容易写了个暴力法,结果还给我整超时了,我那个无语啊!
思路二:动态规划
假如计划在第 i 天卖出股票,那么最大利润的差值一定是在[0, i-1] 之间选最低点买入;所以遍历数组,依次求每个卖出时机的的最大差值,再从中取最大值。
我们可以定义状态,dp[i] 表示第i天卖出股票可以获得的最大利润。
这道题可以参考leetcode 53 最大子序和 和leetcode 300最长递增子序列 ,我的动态规划的题解里面有写道,很重要!
题解超级详细!
题解一:二维数组
- 判定特例
- 状态的定义
- 结果为什么返回的是最后一个
/**
* dp[i][j] 下标为i的这一天,手上的持股状态j 我们的拥有的现金数量
*
* j = 0 不持股
* j = 1 持股
*
* 时间和空间复杂度 都是 o(n)
*
* @param prices
* @return
*/
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0;
}
int[][] dp = new int[len][2];
dp[0][0] = 0;
因为这里负数的设置就可以保证 卖出的价格一定比买入的大 而不会出现只找差值最大的情况
dp[0][1] = -prices[0];
for(int i = 1 ; i < len;i++){
//第i不持股 -- 如何做到只买一次 - 做到只卖一次就可以啦!
// 这里dp[i - 1][1] + prices[i]为什么能保证卖了一次,
// 因为下面一行代码买的时候已经保证了只买一次,所以这里自然就保证了只卖一次,
// 不管是只允许交易一次还是允许交易多次,这行代码都不用变,
// 因为只要保证只买一次(保证了只卖一次)或者买多次(保证了可以卖多次)即可。
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
//为什么不是这么写的呢?
//第i天持股
//dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] - prices[i]);
// - prices[i]这里可以理解为dp[0][0] - prices[i],
// 这里为什么是dp[0][0] - prices[i],因为只有这样才能保证只买一次,
// 所以需要用一开始初始化的未持股的现金dp[0][0]减去当天的股价
//
// 如果题目允许交易多次,就说明可以从直接从昨天的未持股状态变为今天的持股状态,
// 因为昨天未持股状态可以代表之前买过又卖过后的状态,也就是之前交易过多次后的状态。也就是下面的代码。
// dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[0][0] - prices[i]);
}
//返回最后一天 不持股的状态
return dp[len-1][0];
}
}
题解二: 滚动数组优化
坑点注意dp[0][0] 会变化的!
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0;
}
int[][] dp = new int[2][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i =1 ;i < len;i++){
dp[i%2][0] = Math.max(dp[i-1&1][0],dp[i-1&1][1]+prices[i]);
//这里不可以写dp[0][0]因为滚动的原因一直在变化
//dp[i%2][1] = Math.max(dp[(i-1)&1][1],dp[0][0]-prices[i]);
dp[i%2][1] = Math.max(dp[i-1&1][1],-prices[i]);
}
return dp[len-1&1][0];
}
}
题解三:一维数组
/**
* 一维数组优化
*
* 空间优化 降低维度 只看状态转移方程
*
* 下标为 i 行的并且状态是 0 的只参考上一行的 状态0 和1 的行
* 下标为 i 行的并且状态是 1 的只参考了上一行状态为1 的行
*/
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0;
}
//只表示两种状态 0 不持股 1 持股
int[] dp = new int[2];
dp[0] = 0;
dp[1] = -prices[0];
for(int i = 1 ;i < len;i++){
dp[0] = Math.max(dp[0],dp[1]+prices[i]);
dp[1] = Math.max(dp[1],-prices[i]);
}
return dp[0];
}
}
重塑矩阵

这个题没什么需要注意的。一个技巧得到原数组的行和列的位置 除得行 取模得列
class Solution {
public int[][] matrixReshape(int[][] mat, int r, int c) {
//首先通过比较两个矩阵的元素个数来判断是否可以进行转换
int row = mat.length;
int column = mat[0].length;
if( row * column != r * c ){
return mat;
}
//用一个下标 cur 表示当前遍历到的原始矩阵
int[][] res = new int[r][c];
int cur = 0;
for(int i = 0;i < r ;i++){
for(int j = 0 ; j < c ;j++){
res[i][j] = mat[cur/column ][ cur % column];
cur++;
}
}
return res;
}
}
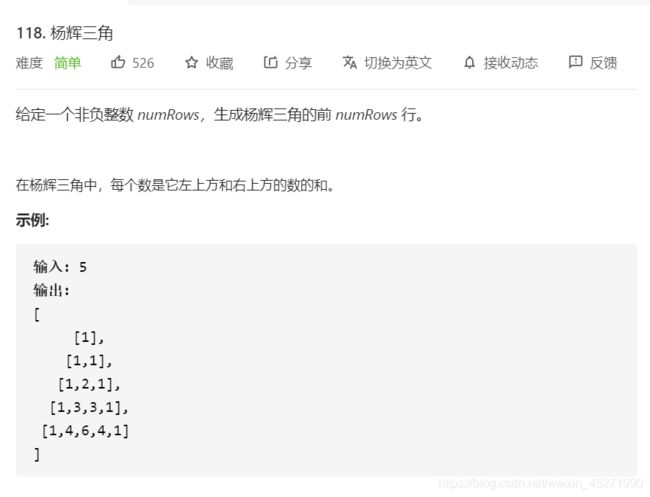
杨辉三角
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new LinkedList<>();
for(int i = 0 ;i < numRows; i++){
List<Integer> temp = new LinkedList<>();
List<Integer> last = new LinkedList<>();
if(i != 0) {
last = res.get(i-1);
}
for(int j = 0 ; j <= i; j++){
if(j == 0|| j == i ){
temp.add(1);
}else{
temp.add(last.get(j-1)+ last.get(j));
}
}
res.add(temp);
}
return res;
}
}
有效的数独
这个题的精妙之处就是要做到一次遍历数独,可以判断是否重复。
使用哈希表和下标的是一个巧妙运算
尤其是这里的下标的计算技巧很常见!
class Solution {
public boolean isValidSudoku(char[][] board) {
int[][] rows = new int[9][9];//初始化都是0 [1][5] = 1 就代表第二行 出现了6这个数字
int[][] col = new int[9][9];//[1][5] = 1 就代表第二列出现了6这个数字
int[][] sbox = new int[9][9];//[1][5] = 1 就代表第二个子数独出现了6这个数字
for(int i = 0 ; i < 9;i++){
for(int j = 0 ; j < 9 ;j++){
if(board[i][j] != '.'){
int num = board[i][j] - '0'-1;
if(rows[i][num] == 1 || col[j][num] == 1 || sbox[ (i / 3 ) * 3 + j / 3][num] == 1){ //说明这个下标以及存放过数字了
return false;
}else{
rows[i][num] = 1;
col[j][num] = 1;
sbox[ (i / 3 ) * 3 + j / 3][num] = 1;
}
}
}
}
return true;
}
}
矩阵置零(※)

思路一:使用标记数组的做法
注意数组的开辟空间,使用一个记忆数组的方式 如果记忆数组开辟的是和原数组的大小和一样的其实没有必要
因为要设置的是这一行一列是0 所有只用记录这一行 或者这一列是否有0就可以了,而不用记录这一行中的哪一列为0。
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
//使用一个记忆数组的方式 如果记忆数组开辟的是和原数组的大小和一样的其实没有必要
//因为要设置的是这一行一列是0 所有只用记录这一行 或者这一列是否有0就可以了
//而不用记录这一行中的那一列为0
boolean[] level = new boolean[m];
boolean[] column = new boolean[n];
for(int i = 0; i< m;i++){
for(int j = 0 ;j < n;j++){
if(matrix[i][j] == 0){
level[i] = true;
column[j] = true;
}
}
}
for(int i = 0; i < m;i++){
for(int j = 0 ; j < n;j++){
if(level[i] ||column[j]){
matrix[i][j] = 0;
}
}
}
}
}
思路二: 原地的以及数组+ 两个标记变量
不用开辟额外的空间,而是使用原数组的第一行和第一列作为记忆数组。然后使用两个额外的变量,来记录原始的第一行和第一列是否出现了0。
每一行的第一个记录改行是否出现了0
每一列的第一个记录该列是否出现了0
在根据记忆数组返回来设置数组
由于这样的做法,原始数据会被覆盖也就是说 可能第一行第一列可能也要设置为0,那么久提前记录一下。
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
boolean flagRow = false;
boolean flagCol = false;
//首先遍历第一行和第一列是否有 0
for (int j = 0 ;j < n;j++){
if(matrix[0][j] == 0){
flagRow = true;
}
}
for(int i = 0; i< m;i++){
if(matrix[i][0] == 0){
flagCol = true;
}
}
//遍历数据 找到了0 就在记忆数组里面更新
for(int i = 1; i < m;i++){
for(int j = 1; j < n;j++){
if(matrix[i][j] == 0){
//表示在原数组第0行 记录第i行是否有0 设置为0
// 但是人家如果如果原来的[0] [j]位置本身就是0 由于flag 遍历已经记录了行 当前位置存储当前列是否要变为0 即可 不矛盾
matrix[i][0] = matrix[0][j] = 0;
}
}
}
//然后在根据第0 和 第0 列的记忆 进行一个重新设置数组
for(int i = 1; i < m ;i++){
for(int j = 1 ; j < n ;j++){
if(matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
//最后在根据两个初始的记忆设置
if(flagRow){
for(int j = 0 ; j < n; j++){
matrix[0][j] = 0;
}
}
if(flagCol){
for(int i = 0; i < m; i++){
matrix[i][0] = 0;
}
}
}
}