Topic 12 临床预测模型之列线表 (Nomogram)
点击关注,桓峰基因
在临床上列线表已经占据大样本临床研究的半壁江山,非常流行,这个简单的回归模型结合临床上大规模的研究数据,发一篇10+还是非常轻松的!
前言
线图(Alignment Diagram),又称诺莫图(Nomogram图),它是建立在多因素回归分析的基础上,将多个预测指标进行整合,然后采用带有刻度的线段,按照一定的比例绘制在同一平面上,从而用以表达预测模型中各个变量之间的相互关系。
列线图的基本原理,简单的说,就是通过构建多因素回归模型(常用的回归模型,例如Cox回归、Logistic回归等),根据模型中各个影响因素对结局变量的贡献程度(回归系数的大小),给每个影响因素的每个取值水平进行赋分,然后再将各个评分相加得到总评分,最后通过总评分与结局事件发生概率之间的函数转换关系,从而计算出该个体结局事件的预测值。列线图将复杂的回归方程,转变为了可视化的图形,使预测模型的结果更具有可读性,方便对患者进行评估。正是由于列线图这种直观便于理解的特点,使它在医学研究和临床实践中也逐渐得到了越来越多的关注和应用。
我们可以看到列线图主要由左边的名称以及右边对应的带有刻度的线段所组成。
列线图的名称主要包括三类:
1. 预测模型中的变量名称:例如图中的年龄(Age)、高血压(Hypertension)、糖尿病(Diabetes)等信息,每一个变量对应的线段上都标注了刻度,代表了该变量的可取值范围,而线段的长度则反映了该因素对结局事件的贡献大小。
2. 得分,包括单项得分,即图中的Point,表示每个变量在不同取值下所对应的单项分数,以及总得分,即Total Point,表示所有变量取值后对应的单项分数加起来合计的总得分。
3. 预测概率:例如图中的5-year survival prob,表示5年的生存概率。
举一个网络上的例子吧,现在假设一名优秀的心内科医生,有这样一位患者,男性,60岁,吸烟,有高血压和糖尿病史,血脂异常,否认CAD家族史,冠状动脉钙化评分(CACS)为3分。咖作为接诊医生,在和患者交代病情的时候,为了向患者说明疾病的严重性,就拿出了这张列线图,自信满满的告诉这位患者,以他目前的疾病状态,预测未来5年、10年和15年的生存概率分别是71%、48%和27%。
那么,小咖是怎么算出来的呢?其实很简单,比如该患者年龄为60岁,我们就在列线图年龄为60岁的地方向上画一条垂直线,即可得到其对应的得分(Points)约为55分。同样性别为男性,对应的分数为1分,以此类推,找出每个变量状态下对应的得分。
最后将所有变量的得分相加,得到患者的总得分(Total Points)约为165.5分,并以总得分为基础,再向下画一条垂直线,就可以知道该患者对应的未来5年、10年和15年的生存率了,是不是很简单很容易理解呢!
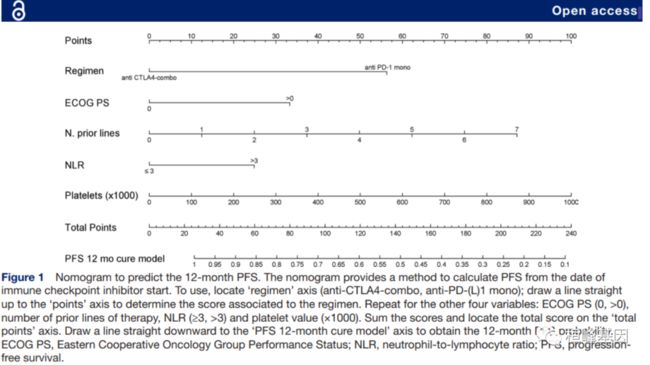
我们看下 IF 10+ 文章中的列线表的角色和地位,找一篇临床医学的高分文章看看,就这篇吧,如下:
列下图文中的位置,Figure ,如下:
Cox 回归模型
Cox 回归在 survival 和 rms 这两个包中都可以实现,因此我们两个函数都进行尝试一下,比较一下两个函数之间的区别。加载 survival 和 rms 程序包,如下:
if (!require(survival)) {
install.packages("survival")
}
if (!require("rms")) {
install.packages("rms")
}
library(survival)
library(rms)
1. 数据读取
我们仍然采用软件包自带的肺癌数据库 NCCTG Lung Cancer Data 作为输入数据,如下:
Descrption
Survival in patients with advanced lung cancer from the North Central Cancer Treatment Group. Performance scores rate how well the patient can perform usual daily activities.
data(package = "survival")
# 2. 打包数据
lung$sex = factor(lung$sex)
dd <- datadist(lung)
options(datadist = "dd")
head(dd)
## $limits
## inst time status age sex ph.ecog ph.karno pat.karno
## Low:effect 3 166.75 1 56 0 75 70
## Adjust to 11 255.50 1 63 1 1 80 80
## High:effect 16 396.50 2 69 1 90 90
## Low:prediction 1 31.00 1 44 1 0 60 60
## High:prediction 26 740.00 2 76 2 2 100 100
## Low 1 5.00 1 39 1 0 50 30
## High 33 1022.00 2 82 2 3 100 100
## meal.cal wt.loss
## Low:effect 635.0000 0.00000
## Adjust to 975.0000 7.00000
## High:effect 1150.0000 15.75000
## Low:prediction 312.4361 -5.00000
## High:prediction 1500.0000 35.23348
## Low 96.0000 -24.00000
## High 2600.0000 68.00000
##
## $values
## $values$status
## [1] 1 2
##
## $values$sex
## [1] "1" "2"
##
## $values$ph.ecog
## [1] 0 1 2 3
##
## $values$ph.karno
## [1] 50 60 70 80 90 100
##
## $values$pat.karno
## [1] 30 40 50 60 70 80 90 100
2. cph {rms}
使用rms 程序包中的 cph 函数构造Cox 回归模型,其中的几个变量需要根据之前做Cox回归模型时显著的那几个变量,然后做Cox回归,我们发现 sex 和 ph.ecog 两个变量显著性最高,如下:
cph <- cph(Surv(time, status) ~ age + sex + ph.ecog + ph.karno, data = lung, x = TRUE,
y = TRUE, surv = TRUE)
cph
## Frequencies of Missing Values Due to Each Variable
## Surv(time, status) age sex ph.ecog
## 0 0 0 1
## ph.karno
## 1
##
## Cox Proportional Hazards Model
##
## cph(formula = Surv(time, status) ~ age + sex + ph.ecog + ph.karno,
## data = lung, x = TRUE, y = TRUE, surv = TRUE)
##
##
## Model Tests Discrimination
## Indexes
## Obs 226 LR chi2 31.27 R2 0.129
## Events 163 d.f. 4 Dxy 0.263
## Center 2.2049 Pr(> chi2) 0.0000 g 0.550
## Score chi2 31.06 gr 1.732
## Pr(> chi2) 0.0000
##
## Coef S.E. Wald Z Pr(>|Z|)
## age 0.0129 0.0094 1.37 0.1712
## sex=2 -0.5726 0.1692 -3.38 0.0007
## ph.ecog 0.6329 0.1760 3.60 0.0003
## ph.karno 0.0126 0.0095 1.32 0.1870
##
3. coxph {survival}
使用survival程序包中的 coxph 函数构造 Cox 回归模型,选择同样的几个变量,然后做Cox回归,同样,我们发现 sex 和 ph.ecog 两个变量显著性最高,但是这个函数会给出一个对整体模型的评估 (p=2.695e-06),如下:
coxph <- coxph(Surv(time, status) ~ age + sex + ph.ecog + ph.karno, data = lung)
coxph
## Call:
## coxph(formula = Surv(time, status) ~ age + sex + ph.ecog + ph.karno,
## data = lung)
##
## coef exp(coef) se(coef) z p
## age 0.012868 1.012951 0.009404 1.368 0.171226
## sex2 -0.572802 0.563943 0.169222 -3.385 0.000712
## ph.ecog 0.633077 1.883397 0.176034 3.596 0.000323
## ph.karno 0.012558 1.012637 0.009514 1.320 0.186842
##
## Likelihood ratio test=31.27 on 4 df, p=2.695e-06
## n= 226, number of events= 163
## (因为不存在,2个观察量被删除了)
实例解析
1. nomogram {rms}
这个rms 程序包里面的nomogram 函数读入的数据需要是rms构建的回归模型,当然这个包里面的模型构建函数还是很全的,基本上可以满足需求,如下描述:
fit a regression model fit that was created with rms, and (usually) with options(datadist = “object.name”) in effect.
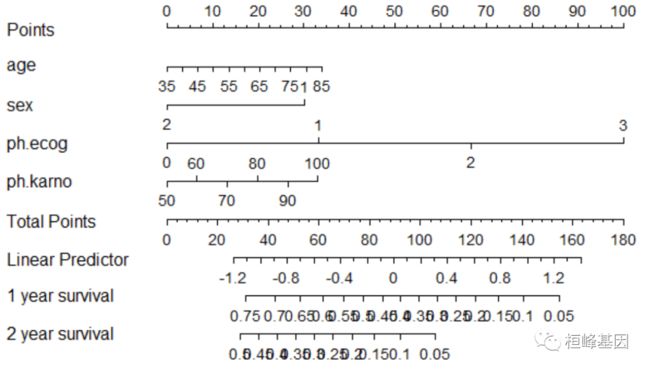
根据 rms 包中函数cph获得的回归模型,绘制列线表,这里选择 1年和2年的风险估计,
如下:
# 绘制列线图\t\t\t
survival <- Survival(cph)
survival1 <- function(x) survival(365, x)
survival2 <- function(x) survival(730, x)
nom <- nomogram(cph, fun = list(survival1, survival2), fun.at = c(0.05, seq(0.1,
0.9, by = 0.05), 0.95), funlabel = c("1 year survival", "2 year survival"))
plot(nom)
2. regplot {regplot}
从下面的表述,我们可知该函数接受多种函数建立的模型,包括cph和coxph等。
Creates a nomogram representation of a fitted regression. The regression object reg can be of different types from the stats, survival , rms, MASS and lme4 libraries. Specifically models generated by the commands: glm, Glm, lm, ols, lrm, survreg, psm, coxph, cph, glm.nb, polr or mixed model regressions lmer, glmer, and glmer.nb. For glm, Glm and glmer the supported family/link pairings are: gaussian/identity, binomial/logit, quasibinomial/logit, poisson/log and quasipoisson/log. For ordinal regression, using polr, logit and probit models are supported. For survreg and psm the distribution may be lognormal, gaussian, weibull, exponential or loglogistic. For glm.nb (from package MASS) and glmer.nb only log-link is allowed.
程序包安装及加载,如下:
if (!require(regplot)) {
install.packages("regplot")
}
library(regplot)
此时我们选择 coxph 构造的回归模型,该函数同时输出每个变量对应的得分 points, 最后我们来绘制列线表,如下:
regplot(coxph,
#对观测2的六个指标在列线图上进行计分展示
observation=lung[6,], #也可以不展示
points=TRUE,
plots=c("density","no plot"),
#预测1年和2年的死亡风险,此处单位是day
failtime = c(365,730),
odds=F,
droplines=F,
leftlabel=T,
prfail = TRUE, #cox回归中需要TRUE
showP = T, #是否展示统计学差异
#droplines = F,#观测2示例计分是否画线
# colors = mycol, #用前面自己定义的颜色
rank="range", #根据统计学差异的显著性进行变量的排序
interval="confidence",
title="Cox regression"
) #展示观测的可信区间
## [[1]]
## ph.karno Points
## 1 50 10
## 2 70 24
## 3 90 37
##
## [[2]]
## ph.ecog Points
## 1 0.0 0
## 2 0.5 17
## 3 1.0 33
## 4 1.5 50
## 5 2.0 67
## 6 2.5 83
## 7 3.0 100
##
## [[3]]
## sex Points
## sex1 1 32
## sex2 2 1
##
## [[4]]
## age Points
## 1 35 13
## 2 45 20
## 3 55 27
## 4 65 33
## 5 75 40
## 6 85 47
##
## [[5]]
## Total Points Pr( time < 365 )
## 1 40 0.1913
## 2 60 0.2669
## 3 80 0.3648
## 4 100 0.4850
## 5 120 0.6210
## 6 140 0.7579
## 7 160 0.8743
## 8 180 0.9518
## 9 200 0.9881
## 10 220 0.9985
结果解读
根据模型中各个影响因素对结局变量的贡献程度(回归系数的大小),给每个影响因素的每个取值水平进行赋分,然后再将各个评分相加得到总评分,最后通过总评分与结局事件发生概率之间的函数转换关系,从而计算出该个体结局事件的预测值。列线图将复杂的回归方程,转变为了可视化的图形,使预测模型的结果更具有可读性,方便对患者进行评估。正是由于列线图这种直观便于理解的特点,使它在医学研究和临床实践中也逐渐得到了越来越多的关注和应用。
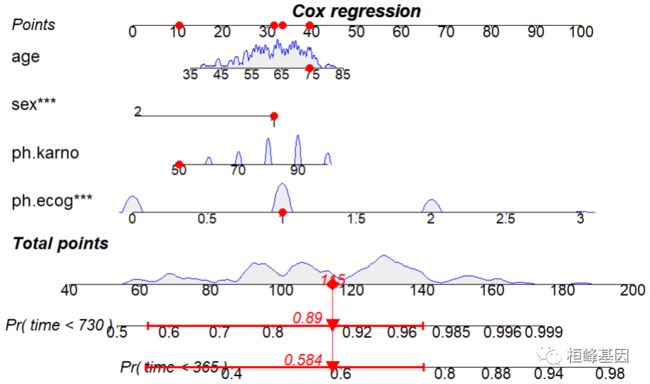
再看我们选择了第六个患者,预测其罹患肺癌的风险,患者信息,模型中涉及到的变量为四个,分别为 sex, age, ph.ecog, ph.karno,regplot函数输出了每个变量的points, 我们自己同样可以清晰的计算出来,如下:
lung[6, ]
## inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
## 6 12 1022 1 74 1 1 50 80 513 0
**解释:**假设有一个患者,年龄74,性别是1,ph.ecog是1,ph.karno是50,在图上找到各个点,对应上方Point的值,将所有的值相加(本处只是讲解大概的值,具体数值应该在模型中计算:Total Points=40+32+33+10=115)。在Total中我们可以看到,115对应的1年和2年的生存率分别约为0.584和0.89。这就进一步说明Nomogram图的内容,本质就是对模型各个参数的一个直观展示。
关注公众号,每日更新,扫码进群交流不停歇,马上就出视频版,关注我,您最佳的选择!
References:
-
Iasonos A, Schrag D, Raj GV, Panageas KS. How to build and interpret a nomogram for cancer prognosis. J Clin Oncol. 2008;26(8):1364-1370.
-
Harrell FE Jr: Regression Modeling StrategiesWith Applications to Linear Models, Logistic Regres-sion, and Survival Analysis. New York, NY, SpringerVerlag, 2001.
-
Pencina MJ, D’Agostino RB: Overall C as ameasure of discrimination in survival analysis:Model specific population value and confidenceinterval estimation. Stat Med 23:2109-2123, 2004.
-
Scrucca L., Santucci A., Aversa F. (2007) Competing risks analysis using R: an easy guide for clinicians. Bone Marrow Transplantation, 40, 381-387.
-
Scrucca L., Santucci A., Aversa F. (2010) Regression modeling of competing risk using R: an in depth guide for clinicians. Bone Marrow Transplantation, 45, 1388–1395.
-
Geskus RB. Cause-specific cumulative incidence estimation and the fine and gray model under both left truncation and right censoring. Biometrics 2011;67:39-49.
-
Zhang Z, Cortese G, Combescure C, Marshall R, Lee M, Lim HJ, Haller B; written on behalf of AME Big-Data Clinical Trial Collaborative Group. Overview of model validation for survival regression model with competing risks using melanoma study data. Ann Transl Med 2018;6(16):325. doi: 10.21037/atm.2018.07.38.