2023华数杯数学建模竞赛选题建议
提示:DS C君认为的难度:C
A题:隔热材料的结构优化控制研究
A题是数模类赛事很常见的物理类赛题,需要学习不少相关知识。
其中第一问需要建立平纹织物整体热导率与单根纤维热导率之间关系的数学模型,并计算出单根A纤维的热导率。问题二是如何选用单根A纤维的直径和调整织物的经密纬密弯曲角度,使得织物的整体热导率最低。
对于前两问,大家可以采用传热模型:基于纤维传热和空隙中气体传热的理论,建立平纹织物的整体热导率与单根纤维热导率之间的关系模型。可以考虑使用传热方程和热传导模型以及多孔介质传热模型。然后进行参数拟合,也就是利用附件2提供的实验样品参数条件下测得的平纹织物的整体热导率,采用参数拟合或优化算法,将实验数据与理论模型进行匹配,得到单根A纤维的热导率。最后进行验证和评估,即根据建立的数学模型和计算得到的单根A纤维的热导率,对模型进行验证并进行评估。可以比较模型计算结果与实验数据的拟合程度,评估模型的准确性和可靠性。
这道题专业性较高,后续账号会在出本题具体思路分析时,再进行具体分析与建模。开放程度低,难度适中。但这类赛题通常不能起到好的练手作用,小白谨慎选择。DS-C君建议物理、电气、自动化等相关专业选择。
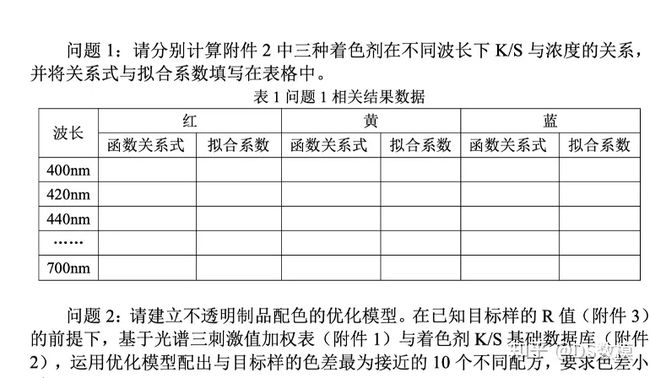
B题:不透明制品最优配色方案设计
B题需要用到不少运筹学相关算法,目测需要用到比如多目标优化、动态规划等,推荐利用lingo进行求解。
这里对第一问进行简单的分析,后续账号会在出本题具体思路分析时,再进行具体分析与建模。
问题一需要计算附件2中三种着色剂在不同波长下的KS值与浓度的关系。首先,我们需要选择适当的拟合函数,常见的选择包择多项式拟合、指数拟合、对数拟合等。在这里,我们使用多项式拟合来表示KS值与浓度的关系。这里的多项式拟合,如果大家想简单一点,可以就用多元线性回归或者二次多项式拟合,推荐利用matlab或者python做拟合。
具体步骤如下所示:
1 根据附件2中的数据,将波长和KS值与浓度分别记为 x 和 y
2 选择一个合适的多项式拟合函数形式
3 将拟合函数带入到拟合问题中,得到一个最小化误差的目标函数
4 使用最小二乘法或其他拟合方法求解该目标函数,得到拟合系数。
综上所述,通过拟合过程,我们可以得到红黄蓝三种着色剂在不同波长下的KS值与浓度的关系,并将关系式和拟合系数填写在表格中(表1)。具体的计算过程需要根据附件2中的数据和所选择的拟合函数进行实施。
这里给大家一个使用Python进行二次多项式拟合的示例代码:
import numpy as np
from scipy.optimize import curve_fit
# 读取附件2中的数据
data = np.loadtxt('附件2.txt', skiprows=1, delimiter='\t')
wavelengths = data[:, 0] # 波长
concentrations = data[:, 1] # 浓度
ks_values = data[:, 2:] # KS值
# 定义二次多项式函数模型
def quadratic_function(x, a, b, c):
return a + b*x + c*x**2
# 对三种着色剂分别进行拟合
fit_params = []
for ks in ks_values.T:
params, _ = curve_fit(quadratic_function, wavelengths, ks)
fit_params.append(params)
# 打印拟合系数
print('拟合系数:')
for i, params in enumerate(fit_params):
print(f'着色剂 {i+1}: a={params[0]}, b={params[1]}, c={params[2]}')
当然,最好在拟合后将拟合结果绘图,如下是绘图代码:
import numpy as np
import matplotlib.pyplot as plt
# 读取附件2中的数据
data = np.loadtxt('附件2.txt', skiprows=1, delimiter='\t')
wavelengths = data[:, 0] # 波长
concentrations = data[:, 1] # 浓度
ks_values = data[:, 2:] # KS值
# 定义二次多项式函数模型
def quadratic_function(x, a, b, c):
return a + b*x + c*x**2
# 对三种着色剂分别进行拟合
fit_params = []
for ks in ks_values.T:
params, _ = curve_fit(quadratic_function, wavelengths, ks)
fit_params.append(params)
# 绘制拟合结果图
fig, axs = plt.subplots(3, 1, figsize=(10, 15))
colors = ['red', 'yellow', 'blue']
for i, ax in enumerate(axs):
ax.scatter(wavelengths, ks_values[:, i], color='black', label='实际值')
ax.plot(wavelengths, quadratic_function(wavelengths, *fit_params[i]), color=colors[i], label='拟合曲线')
ax.set_xlabel('波长')
ax.set_ylabel('KS值')
ax.set_title(f'着色剂 {i+1}')
ax.legend()
plt.tight_layout()
plt.show()
这道题存在最优解,开放程度低,难度适中。大家选择此题最好在做完后,线上线下对对答案。推荐统计学、数学、物理等专业同学选择。
C题:母亲身心健康对婴儿成长的影响
这道题目是典型的数据分析+建模类题目。需要一定的建模能力,和国赛等其他赛事赛题类型类似,建议大家(各个专业均可)进行选择。
题目需要建立数学模型,大家可以使用评价类算法,比如灰色综合评价法、模糊综合评价法对各个指标建立联系。
第一问前大家需要对数据进行分析和数值化处理,也就是EDA(探索性数据分析)。对于数值型数据,大家用归一化、去除异常值等方式就可以进行数据预处理。而对于非数值型数据进行量化,大家可以使用以下方法:
1标签编码
标签编码是将一组可能的取值转换成整数,从而对非数值型数据进行量化的一种方法。例如,在机器学习领域中,对于一个具有多个类别的变量,我们可以给每个类别赋予一个唯一的整数值,这样就可以将其转换为数值型数据。
2独热编码onehot
独热编码是将多个可能的取值转换成二进制数组的一种方法。在独热编码中,每个可能取值对应一个长度为总共可能取值个数的二进制数组,其中只有一个元素为1,其余元素均为0。例如,对于一个性别变量,可以采用独热编码将“男”和“女”分别转换为[1, 0]和[0, 1]。
3分类计数
分类计数是将非数值型数据转换为数值型数据的一种简单方法。在分类计数中,我们根据某些特定属性(比如学历、职业等)来对数据进行分类,然后统计每个类别的数量或频率。例如,在调查问卷中,我们可以对某个问题的回答按照“是”、“否”和“不确定”三个类别进行分类,并计算每个类别的数量或频率。
4主成分分析
主成分分析是将多维数据转换为低维度表示的一种方法。在主成分分析中,我们通过找到最能解释数据变异的主成分来对原始数据进行降维处理。这样就可以将非数值型数据转换为数值型数据。
而第一问建议大家使用一些可视化方法,可以使用常见的EDA可视化方法:
l 直方图和密度图:展示数值变量的分布情况。
l 散点图:展示两个连续变量之间的关系。
l 箱线图:展示数值变量的分布情况和异常值。
l 条形图和饼图:展示分类变量的分布情况。
l 折线图:展示随时间或顺序变化的趋势。
l 热力图:展示不同变量之间的相关性。
l 散点矩阵图:展示多个变量之间的散点图矩阵。
l 地理图:展示地理位置数据和空间分布信息。
而第一问可以给小白先提示下,后续我们还会更新具体的每问思路。第一问是需要我们做相关性分析,看那几个指标之间的相关系数是否高,如果高则代表影响较大,低代表影响较小。这里可以用热力图进行绘制,从而可视化影响程度。
由于这篇是选题建议,详细思路可以看我的后续文章/视频。就不赘述了。这道题目开放度较高,难度较易,是本次比赛练手和获奖的首选题目。推荐所有专业同学选择。
有关思路、相关代码、讲解视频、参考文献等相关内容可以点击下方群名片哦!