【学习强化学习】六、DQN算法原理及实现
文章目录
- 参考资料
- 前言
- 1. State Value Function
-
- 1.1 State Value Function Estimation
-
- 1.1 Monte-Carlo(MC)-based
- 1.2 TD-based
- 1.3 MC 跟 TD 有什么样的差别
- 1.3.1 方差
- 1.3.2 评估结果不同
- 2. State-action Value Function(Q-function)
-
- 2.1 Q函数作用机理分析
- 2.2 通过Q函数找最优策略
-
- 2.2.1 为什么用 Q π ( s , a ) Q^{\pi}(s,a) Qπ(s,a)决定出来的 π ′ \pi' π′一定会比 π \pi π 好。
- 3. tips:Target Network
-
- 3.1 为什么要引入target network
- 4. tips:Exploration
-
- 4.1 exploration的必要性
- 4.2 解决方法一:Epsilon Greedy
- 4.2 解决方法二:Boltzmann Exploration
- 5. tips:Experience Replay
-
- 5.1 怎么借助buffer训练 Q 的模型
- 5.2 使用Experience Replay(经验回放)有什么好处?
- 6. DQN
-
- 6.1 DQN 和 Q-learning 有什么不同?
- 7. 练习
-
- 7.1 简答
- 7.2 问答
-
- 1. 为什么在DQN中采用价值函数近似(Value Function Approximation)的表示方法?
- 2. critic output通常与哪几个值直接相关?
- 3. 我们通常怎么衡量state value function V π ( s ) V^{\pi}(s) Vπ(s)?分别的优势和劣势有哪些?
- 4. 随机性策略和确定性策略有什么区别吗?
- 5. 不打破数据相关性,神经网络的训练效果为什么就不好?
参考资料
https://datawhalechina.github.io/easy-rl/#/chapter6/chapter6
算法实现见github仓库
前言
-
传统的强化学习算法会使用表格的形式存储状态值函数 V ( s ) V(s) V(s) 或状态动作值函数 Q ( s , a ) Q(s,a) Q(s,a),但是这样的方法存在很大的局限性。例如:现实中的强化学习任务所面临的状态空间往往是连续的,存在无穷多个状态,在这种情况下,就不能再使用表格对值函数进行存储。值函数近似利用函数直接拟合状态值函数或状态动作值函数,减少了对存储空间的要求,有效地解决了这个问题。
-
为了在连续的状态和动作空间中计算值函数 Q π ( s , a ) Q^{\pi}(s,a) Qπ(s,a),我们可以用一个函数 Q ϕ ( s , a ) Q_{\phi}(\boldsymbol{s},\boldsymbol{a}) Qϕ(s,a)来表示近似计算,称为价值函数近似(Value Function Approximation)。
Q ϕ ( s , a ) ≈ Q π ( s , a ) Q_{\phi}(\boldsymbol{s}, \boldsymbol{a}) \approx Q^{\pi}(s, a) Qϕ(s,a)≈Qπ(s,a)
其中
s , a \boldsymbol{s},\boldsymbol{a} s,a 分别是状态 s s s 和动作 a a a 的向量表示;
函数 Q ϕ ( s , a ) Q_{\phi}(\boldsymbol{s}, \boldsymbol{a}) Qϕ(s,a) 通常是一个参数为 ϕ \phi ϕ 的函数,比如神经网络,输出为一个实数,称为Q 网络(Q-network)。
1. State Value Function
- 在 value-based 的方法里面,我们学习的不是策略,我们要学习的是一个 critic(评论家)。评论家要做的事情是评价actor现在的行为有多好,即 Policy Evaluation(策略评估)。
- 有一种评论家叫做 state value function(状态价值函数)。评论家的输出值取决于状态和演员。评论家是在衡量某一个演员的好坏,而不是衡量一个状态的好坏。评论家的输出是跟演员有关的,状态的价值其实取决于你的演员,当演员变的时候,状态价值函数的输出其实也是会跟着改变的。
1.1 State Value Function Estimation
怎么衡量这个状态价值函数 V π ( s ) V^{\pi}(s) Vπ(s) 呢?有两种不同的做法:MC-based 的方法和 TD-based 的方法。
1.1 Monte-Carlo(MC)-based
-
Monte-Carlo(MC)-based的方法就是让演员去跟环境做互动,要看演员好不好,我们就让演员去跟环境做互动,给评论家看。然后,评论家就统计说,
- 演员如果看到状态 s a s_a sa,接下来的累积奖励会有多大。
- 如果它看到状态 s b s_b sb,接下来的累积奖励会有多大。
-
但是实际上,我们不可能把所有的状态通通遍历。所以实际上 V π ( s ) V^{\pi}(s) Vπ(s) 是一个网络。对一个网络来说,就算输入状态是从来都没有看过的,它也可以想办法估测一个值。
-
如何训练这个网络?
假设如果在状态 s a s_a sa,接下来的累积奖励是 G a G_a Ga。也就是说,对这个价值函数来说,如果输入是状态 s a s_a sa,正确的输出应该是 G a G_a Ga。如果输入状态 s b s_b sb,正确的输出应该是值 G b G_b Gb。所以在训练的时候, 它就是一个 回归问题(regression problem)。

1.2 TD-based
-
在 MC-based 的方法中,每次我们都要算累积奖励,也就是从某一个状态 s a s_a sa 一直玩到游戏结束的时候,得到的所有奖励的总和。所以你要使用 MC-based 的方法,你必须至少把这个游戏玩到结束。但有些游戏非常长,要玩到游戏结束才能够更新网络,花的时间太长了,因此我们会采用 TD-based 的方法。
-
TD-based 的方法不需要把游戏玩到底,只要在游戏的某一个情况,某一个状态 s t s_t st 的时候,采取动作 a t a_t at 得到奖励 r t r_t rt ,跳到状态 s t + 1 s_{t+1} st+1,就可以使用 TD 的方法。
-
如何使用TD方法?
这边是基于以下这个式子:
V π ( s t ) = V π ( s t + 1 ) + r t V^{\pi}\left(s_{t}\right)=V^{\pi}\left(s_{t+1}\right)+r_{t} Vπ(st)=Vπ(st+1)+rt
假设我们现在用的是某一个策略 π \pi π,在状态 s t s_t st,它会采取动作 a t a_t at,给我们奖励 r t r_t rt ,接下来进入 s t + 1 s_{t+1} st+1 。状态 s t + 1 s_{t+1} st+1 的值跟状态 s t s_t st 的值,它们的中间差了一项 r t r_t rt。有了这个式子以后,你在训练的时候,你并不是直接去估测 V,而是希望你得到的结果 V 可以满足这个式子。
也就是说我们会是这样训练的,我们把 s t s_t st 丢到网络里面,因为 s t s_t st 丢到网络里面会得到 V π ( s t ) V^{\pi}(s_t) Vπ(st),把 s t + 1 s_{t+1} st+1 丢到你的值网络里面会得到 V π ( s t + 1 ) V^{\pi}(s_{t+1}) Vπ(st+1),这个式子告诉我们, V π ( s t ) V^{\pi}(s_t) Vπ(st) 减 V π ( s t + 1 ) V^{\pi}(s_{t+1}) Vπ(st+1)的值应该是 r t r_t rt。然后希望它们两个相减的 loss 跟 r t r_t rt 越接近,训练下去,更新 V 的参数,就可以把 V 函数学习出来。
1.3 MC 跟 TD 有什么样的差别
1.3.1 方差
MC 最大的问题就是方差很大。如果用 TD 的话,你是要去最小化这样的一个式子:

在这中间会有随机性的是 r。因为计算你在 s t s_t st 采取同一个动作,你得到的奖励也不一定是一样的,所以 r 是一个随机变量。但这个随机变量的方差会比 G a G_a Ga 还要小,因为 G a G_a Ga 是很多 r 合起来,这边只是某一个 r 而已。 G a G_a Ga 的方差会比较大,r 的方差会比较小。但是这边你会遇到的一个问题是你这个 V 不一定估得准。假设你的这个 V 估得是不准的,那你使用这个式子学习出来的结果,其实也会是不准的。所以 MC 跟 TD 各有优劣。今天其实 TD 的方法是比较常见的,MC 的方法其实是比较少用的。
1.3.2 评估结果不同
-
假设有某一个评论家,它去观察某一个策略 π \pi π 跟环境互动的 8 个 episode 的结果。有一个演员 π \pi π 跟环境互动了8 次,得到了8 次玩游戏的结果。接下来这个评论家去估测状态的值。
-
我们先计算 s b s_b sb 的值。 状态 s b s_b sb 在 8 场游戏里面都有经历过,其中有 6 场得到奖励 1,有 2 场得到奖励 0。所以如果你是要算期望值的话,就算看到状态 s b s_b sb 以后得到的奖励,一直到游戏结束的时候得到的累积奖励期望值是 3/4,计算过程如下式所示:
6 × 1 + 2 × 0 8 = 6 8 = 3 4 \frac{6 \times 1 + 2 \times 0}{8}=\frac{6}{8}=\frac{3}{4} 86×1+2×0=86=43 -
但 s a s_a sa 期望的奖励到底应该是多少呢?这边其实有两个可能的答案:一个是 0,一个是 3/4。为什么有两个可能的答案呢?这取决于你用 MC 还是TD。用 MC 跟用 TD 算出来的结果是不一样的。
-
假如用 MC 的话,你会发现这个 s a s_a sa 就出现一次,看到 s a s_a sa 这个状态,接下来累积奖励就是 0,所以 s a s_a sa 期望奖励就是 0。
-
但 TD 在计算的时候,它要更新下面这个式子:
V π ( s a ) = V π ( s b ) + r V^{\pi}\left(s_{a}\right)=V^{\pi}\left(s_{b}\right)+r Vπ(sa)=Vπ(sb)+r
因为我们在状态 s a s_a sa得到奖励 r=0 以后,跳到状态 s b s_b sb。所以状态 s b s_b sb的奖励会等于状态 s b s_b sb 的奖励加上在状态 s a s_a sa 跳到状态 s b s_b sb 的时候可能得到的奖励 r。而这个得到的奖励 r 的值是 0, s b s_b sb 期望奖励是 3/4,那 s a s_a sa 的奖励应该是 3/4。 -
用 MC 跟 TD 估出来的结果很有可能是不一样的。就算评论家观察到一样的训练数据,它最后估出来的结果也不一定是一样的。为什么会这样呢?你可能问说,哪一个结果比较对呢?其实就都对。
-
因为在第一个轨迹, s a s_a sa 得到奖励 0 以后,再跳到 s b s_b sb 也得到奖励 0。这边有两个可能。
- 一个可能是: s a s_a sa 是一个标志性的状态,只要看到 s a s_a sa 以后, s b s_b sb 就会拿不到奖励, s a s_a sa 可能影响了 s b s_b sb。如果是用 MC 的算法的话,它会把 s a s_a sa 影响 s b s_b sb 这件事考虑进去。所以看到 s a s_a sa 以后,接下来 s b s_b sb 就得不到奖励, s b s_b sb 期望的奖励是 0。
- 另一个可能是:看到 s a s_a sa 以后, s b s_b sb 的奖励是 0 这件事只是一个巧合,并不是 s a s_a sa 所造成,而是因为说 s b s_b sb 有时候就是会得到奖励 0,这只是单纯运气的问题。其实平常 s b s_b sb 会得到奖励期望值是 3/4,跟 s a s_a sa 是完全没有关系的。所以假设 s a s_a sa 之后会跳到 s b s_b sb,那其实得到的奖励按照 TD 来算应该是 3/4。
-
所以不同的方法考虑了不同的假设,运算结果不同。
2. State-action Value Function(Q-function)
还有另外一种评论家叫做 Q-function。它又叫做state-action value function(状态-动作价值函数)。
- 状态价值函数的输入是一个状态,它是根据状态去计算出,看到这个状态以后的期望的累积奖励( expected accumulated reward)是多少。
- 状态-动作价值函数的输入是一个状态、动作对,它的意思是说,在某一个状态采取某一个动作,假设我们都使用演员 π \pi π ,得到的累积奖励的期望值有多大
2.1 Q函数作用机理分析
Q-function 有两种写法:
虽然表面上我们学习一个 Q-function,它只能拿来评估某一个演员 π \pi π 的好坏,但只要有了这个 Q-function,我们就可以做强化学习。有了这个 Q-function,我们就可以决定要采取哪一个动作,我们就可以进行策略改进(Policy Improvement)。
-
它的原则是这样,假设有一个初始的演员 π \pi π,这个 π \pi π 跟环境互动,会收集数据。接下来学习一个 π \pi π 这个演员的 Q 值,你去衡量一下 π \pi π 在某一个状态强制采取某一个动作, TD 或 MC会得到的期望奖励。学习出一个 Q-function 以后,就可以找到一个新的策略 π ′ \pi' π′ ,policy π ′ \pi' π′ 一定会比原来的策略 π \pi π 还要好(那等一下会定义说,什么叫做好)。然后用 π ′ \pi' π′ 取代 π \pi π,再去找它的 Q-function,得到新的以后,再去找一个更好的策略。这样一直循环下去,policy 就会越来越好。
-
首先要定义的是什么叫做比较好?这边好是说,对所有可能的状态 s 而言, V π ′ ( s ) ≥ V π ( s ) V^{\pi^{\prime}}(s) \geq V^{\pi}(s) Vπ′(s)≥Vπ(s)。也就是说我们走到同一个状态 s 的时候,如果拿 π π \piπ ππ继续跟环境互动下去,我们得到的奖励一定会小于等于用 π ′ \pi' π′ 跟环境互动下去得到的奖励。所以不管在哪一个状态,你用 π ′ \pi' π′ 去做交互,得到的期望奖励一定会比较大。所以 π ′ \pi' π′ 是比 π \pi π 还要好的一个策略。
2.2 通过Q函数找最优策略
-
有了 Q-function 以后,怎么找这个 π ′ \pi' π′ 呢?
π ′ ( s ) = arg max a Q π ( s , a ) \pi^{\prime}(s)=\arg \max _{a} Q^{\pi}(s, a) π′(s)=argamaxQπ(s,a) -
根据上式决定那 π ′ \pi' π′ 一定会比 π \pi π还要好。假设已经学习出 π \pi π 的 Q-function,今天在某一个状态 s,你把所有可能的动作 a 都一一带入这个 Q-function,看看哪一个 a 可以让 Q-function 的值最大,那这个动作就是 π ′ \pi' π′ 会采取的动作。
-
这边要注意一下,给定这个状态 s,你的策略 π \pi π 并不一定会采取动作a,我们是给定某一个状态 s 强制采取动作 a,用 π \pi π 继续互动下去得到的期望奖励,这个才是 Q-function 的定义。所以在状态 s 里面不一定会采取动作 a。用 π ′ \pi' π′ 在状态 s 采取动作 a 跟 π \pi π 采取的动作是不一定会一样的, π ′ \pi' π′ 所采取的动作会让它得到比较大的奖励。
- 所以这个 π ′ \pi' π′ 是用 Q-function 推出来的,没有另外一个网络决定 π ′ \pi' π′ 怎么交互,有 Q-function 就可以找出 π ′ \pi' π′。
- 但是这边有另外一个问题就是,在这边要解一个 arg max 的问题,所以 a 如果是连续的就会有问题。如果是离散的,a 只有 3 个选项,一个一个带进去, 看谁的 Q 最大,没有问题。但如果 a 是连续的,要解 arg max 问题,就会有问题。
2.2.1 为什么用 Q π ( s , a ) Q^{\pi}(s,a) Qπ(s,a)决定出来的 π ′ \pi' π′一定会比 π \pi π 好。
假设有一个策略叫做 π ′ \pi' π′,它是由 Q π Q^{\pi} Qπ 决定的。我们要证对所有的状态 s 而言, V π ′ ( s ) ≥ V π ( s ) V^{\pi^{\prime}}(s) \geq V^{\pi}(s) Vπ′(s)≥Vπ(s)。
怎么证呢?我们先把 V π ( s ) V^{\pi}(s) Vπ(s) 写出来:
V π ( s ) = Q π ( s , π ( s ) ) V^{\pi}(s)=Q^{\pi}(s, \pi(s)) Vπ(s)=Qπ(s,π(s))
假设在状态 s follow π \pi π 这个演员,它会采取的动作就是 π ( s ) \pi(s) π(s),那你算出来的 Q π ( s , π ( s ) ) Q^{\pi}(s, \pi(s)) Qπ(s,π(s))会等于 V π ( s ) V^{\pi}(s) Vπ(s)。一般而言, Q π ( s , π ( s ) ) Q^{\pi}(s, \pi(s)) Qπ(s,π(s)) 不一定等于 V π ( s ) V^{\pi}(s) Vπ(s) ,因为动作不一定是 π ( s ) \pi(s) π(s)。但如果这个动作是 π ( s ) \pi(s) π(s) 的话, Q π ( s , π ( s ) ) Q^{\pi}(s, \pi(s)) Qπ(s,π(s))是等于 V π ( s ) V^{\pi}(s) Vπ(s) 的。
Q π ( s , π ( s ) ) Q Q^{\pi}(s, \pi(s))Q Qπ(s,π(s))Q 还满足如下的关系:
Q π ( s , π ( s ) ) ≤ max a Q π ( s , a ) Q^{\pi}(s, \pi(s)) \le \max _{a} Q^{\pi}(s, a) Qπ(s,π(s))≤amaxQπ(s,a)
因为 a 是所有动作里面可以让 Q 最大的那个动作,所以今天这一项一定会比它大。这一项就是 Q π ( s , a ) Q^{\pi}(s, a) Qπ(s,a), a a a 就是 π ′ ( s ) \pi'(s) π′(s)。因为 π ′ ( s ) \pi'(s) π′(s) 输出的 a a a 就是可以让 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a) 最大的那一个,所以我们得到了下面的式子:
max a Q π ( s , a ) = Q π ( s , π ′ ( s ) ) \max _{a} Q^{\pi}(s, a)=Q^{\pi}\left(s, \pi^{\prime}(s)\right) amaxQπ(s,a)=Qπ(s,π′(s))
于是:
V π ( s ) ≤ Q π ( s , π ′ ( s ) ) V^{\pi}(s) \leq Q^{\pi}\left(s, \pi^{\prime}(s)\right) Vπ(s)≤Qπ(s,π′(s))
在这个状态 s 你故意不按照 π \pi π 所给你指示的方向,而是按照 π ′ \pi' π′ 的方向走一步,但只有第一步是按照 π ′ \pi' π′ 的方向走,只有在状态 s 这个地方,你才按照 π ′ \pi' π′ 的指示走,接下来你就按照 π \pi π 的指示走。虽然只有一步之差, 但是从上面这个式子可知,虽然只有一步之差,但你得到的奖励一定会比完全 follow π \pi π 得到的奖励还要大。
接下来要证下面的式子:
Q π ( s , π ′ ( s ) ) ≤ V π ′ ( s ) Q^{\pi}\left(s, \pi^{\prime}(s) \right) \le V^{\pi'}(s) Qπ(s,π′(s))≤Vπ′(s)
也就是说,只有一步之差,你会得到比较大的奖励。但假设每步都是不一样的,每步都是 follow π ′ \pi' π′ 而不是 π \pi π 的话,那你得到的奖励一定会更大。如果你要用数学式把它写出来的话,你可以写成 Q π ( s , π ′ ( s ) ) Q^{\pi}\left(s, \pi^{\prime}(s)\right) Qπ(s,π′(s)) ,它的意思就是说,我们在状态 s t s_t st 采取动作 a t a_t at,得到奖励 r t r_{t} rt,然后跳到状态 s t + 1 s_{t+1} st+1,即如下式所示:
Q π ( s , π ′ ( s ) ) = E [ r t + V π ( s t + 1 ) ∣ s t = s , a t = π ′ ( s t ) ] Q^{\pi}\left(s, \pi^{\prime}(s)\right)=E\left[r_t+V^{\pi}\left(s_{t+1}\right) \mid s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] Qπ(s,π′(s))=E[rt+Vπ(st+1)∣st=s,at=π′(st)]
在文献上有时也会说:在状态 s t s_t st 采取动作 a t a_t at 得到奖励 r t + 1 r_{t+1} rt+1, 有人会写成 r t r_t rt,但意思其实都是一样的。
因为 V π ( s ) ≤ Q π ( s , π ′ ( s ) ) V^{\pi}(s) \leq Q^{\pi}\left(s, \pi^{\prime}(s)\right) Vπ(s)≤Qπ(s,π′(s)),也就是 V π ( s t + 1 ) ≤ Q π ( s t + 1 , π ′ ( s t + 1 ) ) V^{\pi}(s_{t+1}) \leq Q^{\pi}\left(s_{t+1}, \pi^{\prime}(s_{t+1})\right) Vπ(st+1)≤Qπ(st+1,π′(st+1)),所以我们得到下式:
E [ r t + V π ( s t + 1 ) ∣ s t = s , a t = π ′ ( s t ) ] ≤ E [ r t + Q π ( s t + 1 , π ′ ( s t + 1 ) ) ∣ s t = s , a t = π ′ ( s t ) ] \begin{array}{l} E\left[r_{t}+V^{\pi}\left(s_{t+1}\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\ \leq E\left[r_{t}+Q^{\pi}\left(s_{t+1}, \pi^{\prime}\left(s_{t+1}\right)\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \end{array} E[rt+Vπ(st+1)∣st=s,at=π′(st)]≤E[rt+Qπ(st+1,π′(st+1))∣st=s,at=π′(st)]
因为 Q π ( s t + 1 , π ′ ( s t + 1 ) ) = r t + 1 + V π ( s t + 2 ) Q^{\pi}\left(s_{t+1}, \pi^{\prime}\left(s_{t+1}\right)\right) = r_{t+1}+V^{\pi}\left(s_{t+2}\right) Qπ(st+1,π′(st+1))=rt+1+Vπ(st+2),所以我们得到下式:
E [ r t + Q π ( s t + 1 , π ′ ( s t + 1 ) ) ∣ s t = s , a t = π ′ ( s t ) ] = E [ r t + r t + 1 + V π ( s t + 2 ) ∣ s t = s , a t = π ′ ( s t ) ] \begin{array}{l} E\left[r_{t}+Q^{\pi}\left(s_{t+1}, \pi^{\prime}\left(s_{t+1}\right)\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\ =E\left[r_{t}+r_{t+1}+V^{\pi}\left(s_{t+2}\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \end{array} E[rt+Qπ(st+1,π′(st+1))∣st=s,at=π′(st)]=E[rt+rt+1+Vπ(st+2)∣st=s,at=π′(st)]
然后再代入 V π ( s ) ≤ Q π ( s , π ′ ( s ) ) V^{\pi}(s) \leq Q^{\pi}\left(s, \pi^{\prime}(s)\right) Vπ(s)≤Qπ(s,π′(s)),一直算到回合结束,即:
V π ( s ) ≤ Q π ( s , π ′ ( s ) ) = E [ r t + V π ( s t + 1 ) ∣ s t = s , a t = π ′ ( s t ) ] ≤ E [ r t + Q π ( s t + 1 , π ′ ( s t + 1 ) ) ∣ s t = s , a t = π ′ ( s t ) ] = E [ r t + r t + 1 + V π ( s t + 2 ) ∣ s t = s , a t = π ′ ( s t ) ] ≤ E [ r t + r t + 1 + Q π ( s t + 2 , π ′ ( s t + 2 ) ∣ s t = s , a t = π ′ ( s t ) ] = E [ r t + r t + 1 + r t + 2 + V π ( s t + 3 ) ∣ s t = s , a t = π ′ ( s t ) ] ≤ ⋯ ≤ E [ r t + r t + 1 + r t + 2 + ⋯ ∣ s t = s , a t = π ′ ( s t ) ] = V π ′ ( s ) \begin{aligned} V^{\pi}(s) &\le Q^{\pi}(s,\pi'(s)) \\ &=E\left[r_{t}+V^{\pi}\left(s_{t+1}\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right]\\ &\le E\left[r_{t}+Q^{\pi}\left(s_{t+1}, \pi^{\prime}\left(s_{t+1}\right)\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\ &=E\left[r_{t}+r_{t+1}+V^{\pi}\left(s_{t+2}\right) |s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\ & \le E\left[r_{t}+r_{t+1}+Q^{\pi}\left(s_{t+2},\pi'(s_{t+2}\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\ & = E\left[r_{t}+r_{t+1}+r_{t+2}+V^{\pi}\left(s_{t+3}\right) |s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\ & \le \cdots\\ & \le E\left[r_{t}+r_{t+1}+r_{t+2}+\cdots | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\ & = V^{\pi'}(s) \end{aligned} Vπ(s)≤Qπ(s,π′(s))=E[rt+Vπ(st+1)∣st=s,at=π′(st)]≤E[rt+Qπ(st+1,π′(st+1))∣st=s,at=π′(st)]=E[rt+rt+1+Vπ(st+2)∣st=s,at=π′(st)]≤E[rt+rt+1+Qπ(st+2,π′(st+2)∣st=s,at=π′(st)]=E[rt+rt+1+rt+2+Vπ(st+3)∣st=s,at=π′(st)]≤⋯≤E[rt+rt+1+rt+2+⋯∣st=s,at=π′(st)]=Vπ′(s)
因此:
V π ( s ) ≤ V π ′ ( s ) V^{\pi}(s)\le V^{\pi'}(s) Vπ(s)≤Vπ′(s)
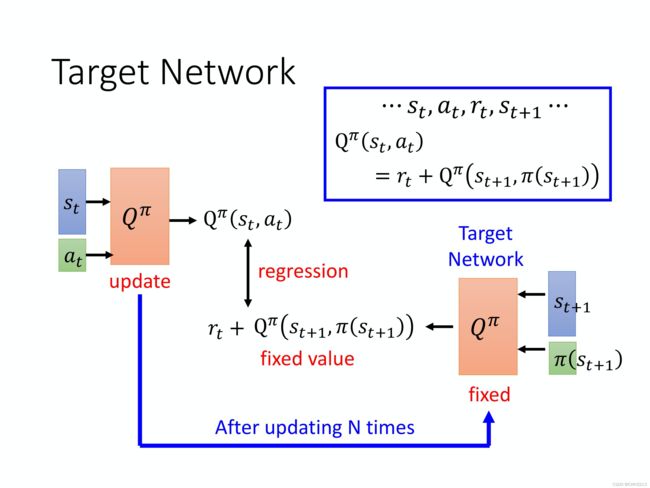
3. tips:Target Network
3.1 为什么要引入target network
我们在学习 Q-function 的时候,也会用到 TD 的概念。
Q π ( s t , a t ) = r t + Q π ( s t + 1 , π ( s t + 1 ) ) \mathrm{Q}^{\pi}\left(s_{t}, a_{t}\right) =r_{t}+\mathrm{Q}^{\pi}\left(s_{t+1}, \pi\left(s_{t+1}\right)\right) Qπ(st,at)=rt+Qπ(st+1,π(st+1))
但是实际上这样的一个输入并不好学习,因为假设这是一个回归问题, Q π ( s t , a t ) \mathrm{Q}^{\pi}\left(s_{t}, a_{t}\right) Qπ(st,at) 是网络的输出, r t + Q π ( s t + 1 , π ( s t + 1 ) ) r_{t}+\mathrm{Q}^{\pi}\left(s_{t+1}, \pi\left(s_{t+1}\right)\right) rt+Qπ(st+1,π(st+1)) 是目标,会发现目标是会动的。当然要实现这样的训练,其实也没有问题,在做反向传播的时候, Q π Q^{\pi} Qπ 的参数被更新,把两个更新的结果加在一起,因为它们是同一个模型 Q π Q^{\pi} Qπ。但这样会导致训练变得不太稳定,因为假设把 Q π ( s t , a t ) \mathrm{Q}^{\pi}\left(s_{t}, a_{t}\right) Qπ(st,at)当作模型的输出, r t + Q π ( s t + 1 , π ( s t + 1 ) ) r_{t}+\mathrm{Q}^{\pi}\left(s_{t+1}, \pi\left(s_{t+1}\right)\right) rt+Qπ(st+1,π(st+1))当作目标的话,要去拟合的目标是一直在变的,这种一直在变的目标的训练是不太好训练的。
所以通常会把右边这个 Q 网络固定住。也就是说在训练的时候,只更新左边的 Q 网络的参数,而右边的 Q 网络的参数会被固定住。因为右边的 Q 网络负责产生目标,所以叫 目标网络。因为目标网络是固定的,所以得到的目标 r t + Q π ( s t + 1 , π ( s t + 1 ) ) r_{t}+\mathrm{Q}^{\pi}\left(s_{t+1}, \pi\left(s_{t+1}\right)\right) rt+Qπ(st+1,π(st+1))的值也是固定的。因为目标网络是固定的,我们只调左边网络的参数,它就变成一个回归问题。我们希望模型的输出的值跟目标越接近越好,只需最小化它的均方误差(mean square error)。
在实现的时候,一般把左边的 Q 网络更新好几次以后,再去用更新过的 Q 网络替换这个目标网络。
初始时这两个网络是一样的,然后在训练的时候,把右边的 Q 网络固定住。在做梯度下降的时候,只调左边这个网络的参数,可能更新 100 次以后才把这个参数复制到右边的网络去。复制过去以后,目标值就变了,接下来就要重新再训练。
我们可以通过猫追老鼠的例子来直观地理解为什么要 fix target network。猫是 Q estimation,老鼠是 Q target。一开始的话,猫离老鼠很远,我们想让这个猫追上老鼠。
因为 Q target 也是跟模型参数相关的,所以每次优化后,Q target 也会动。这就导致一个问题,猫和老鼠都在动。然后它们就会在优化空间里面到处乱动,就会产生非常奇怪的优化轨迹,这就使得训练过程十分不稳定。所以我们可以固定 Q target,让老鼠动得不是那么频繁,可能让它每 5 步动一次,猫则是每一步都在动。如果老鼠每 5 次动一步的话,猫就有足够的时间来接近老鼠。然后它们之间的距离会随着优化过程越来越小,最后它们就可以拟合,拟合过后就可以得到一个好的Q 网络。
4. tips:Exploration
4.1 exploration的必要性
- 当我们使用 Q-function 的时候,policy 完全取决于 Q-function。给定某一个状态,你就穷举所有的 a, 看哪个 a 可以让 Q 值最大,它就是采取的动作。这个跟策略梯度不一样,在做策略梯度的时候,输出其实是随机的。我们输出一个动作的分布,根据这个动作的分布去做采样, 所以在策略梯度里面,你每次采取的动作是不一样的,是有随机性的。
- 像这种 Q-function, 如果采取的动作总是固定的,那么这并不是一个好的收集数据的方式。例如你要估测在某一个状态采取某一个动作会得到的 Q 值,你一定要在那一个状态采取过那一个动作,才估得出它的值。如果你没有在那个状态采取过那个动作,你其实估不出那个值的。如果是用深的网络,就你的 Q-function 是一个网络,这种情形可能会没有那么严重。但是一般而言,假设 Q-function 是一个表格,没有看过的 state-action pair,它就是估不出值来。网络也是会有一样的问题,只是没有那么严重。
4.2 解决方法一:Epsilon Greedy
Epsilon Greedy的意思是说,我们有 1 − ε 1-\varepsilon 1−ε 的概率会按照 Q-function 来决定 动作,通常 ε \varepsilon ε 就设一个很小的值, 1 − ε 1-\varepsilon 1−ε可能是 90%,也就是 90% 的概率会按照 Q-function 来决定 动作,但是你有 10% 的机率是随机的。通常在实现上 ε \varepsilon ε 会随着时间递减。在最开始的时候。因为还不知道那个动作是比较好的,所以你会花比较大的力气在做探索。接下来随着训练的次数越来越多。已经比较确定说哪一个 Q 是比较好的。你就会减少你的探索,你会把 ε \varepsilon ε 的值变小,主要根据 Q-function 来决定你的动作,比较少随机决定动作,这是 Epsilon Greedy。
4.2 解决方法二:Boltzmann Exploration
这个方法就比较像是策略梯度。在策略梯度里面,网络的输出是一个期望的动作空间上面的一个的概率分布,再根据概率分布去做采样。那其实你也可以根据 Q 值 去定一个概率分布,假设某一个动作的 Q 值越大,代表它越好,我们采取这个动作的机率就越高。但是某一个动作的 Q 值小,不代表我们不能尝试。
Q: 我们有时候也要尝试那些 Q 值比较差的动作,怎么做呢?
A: 因为 Q 值是有正有负的,所以可以它弄成一个概率,你先取指数,再做归一化。然后把 exp ( Q ( s , a ) ) \exp(Q(s,a)) exp(Q(s,a)) 做归一化的这个概率当作是你在决定动作的时候采样的概率。在实现上,Q 是一个网络,所以你有点难知道, 在一开始的时候网络的输出到底会长怎么样子。假设你一开始没有任何的训练数据,参数是随机的,那给定某一个状态 s,不同的 a 输出的值可能就是差不多的,所以一开始 Q ( s , a ) Q(s,a) Q(s,a)应该会倾向于是均匀的。也就是在一开始的时候,你这个概率分布算出来,它可能是比较均匀的。
5. tips:Experience Replay
-
Experience Replay 会构建一个 Replay Buffer,Replay Buffer 又被称为 Replay Memory。我们会把所有的数据放到一个 buffer 里面。我们之前在某一个状态 s t s_t st,采取某一个动作 a t a_t at,得到了奖励 r t r_t rt。然后跳到状态 s t + 1 s_{t+1} st+1。用 π \pi π去跟环境互动很多次,把收集到的资料都放到这个 replay buffer 里面。
-
这边要注意是 replay buffer 里面的经验可能是来自于不同的策略,Buffer 只有在它装满的时候,才会把旧的数据丢掉。所以这个 buffer 里面它其实装了很多不同的策略的经验。
5.1 怎么借助buffer训练 Q 的模型
-
有了 buffer 以后,怎么训练 Q 的模型,怎么估 Q-function?做法是这样:迭代地去训练 Q-function,在每次迭代里面,从这个 buffer 里面随机挑一个 batch 出来,就跟一般的网络训练一样,从训练集里面,去挑一个 batch 。根据batch里的数据经验去更新 Q-function。就跟 TD learning 要有一个目标网络是一样的。
-
当我们这么做的时候, 它变成了一个 off-policy 的做法。因为本来我们的 Q 是要观察 π \pi π 的经验,但实际上 replay buffer 里面的这些经验不是通通来自于 π \pi π,有些是过去其他的 π \pi π 所遗留下来的经验。
-
Q:我们明明是要观察 π \pi π 的值,里面混杂了一些不是 π \pi π 的经验,这有没有关系?
-
A:没关系。这并不是因为过去的 π \pi π 跟现在的 π \pi π 很像, 就算过去的 π \pi π 没有很像,其实也是没有关系的。主要的原因是因为, 我们并不是去采样一个轨迹,我们只采样了一笔经验,所以跟是不是 off-policy 这件事是没有关系的。就算是 off-policy,就算是这些经验不是来自于 π \pi π,我们其实还是可以拿这些经验来估测 Q π ( s , a ) Q^{\pi}(s,a) Qπ(s,a)。这件事有点难解释,不过你就记得说 Experience Replay 在理论上也是没有问题的。
5.2 使用Experience Replay(经验回放)有什么好处?
这么做有两个好处:
- 其实在做强化学习的时候, 往往最花时间的步骤是在跟环境做互动,训练网络反而是比较快的。因为用 GPU 训练其实很快, 真正花时间的往往是在跟环境做互动。用 replay buffer 可以减少跟环境做互动的次数,因为在做训练的时候,你的经验不需要通通来自于某一个策略。一些过去的策略所得到的经验可以放在 buffer 里面被使用很多次,被反复的再利用,这样让采样到经验的利用是比较高效的。
- 在训练网络的时候,其实我们希望一个 batch 里面的数据越多样(diverse)越好。如果 batch 里面的数据都是同样性质的,训练下去是容易坏掉的。如果 batch 里面都是一样的数据,训练的时候,performance 会比较差。我们希望 batch 的数据越多样越好。那如果 buffer 里面的那些经验通通来自于不同的策略,那采样到的一个 batch 里面的数据会是比较多样的。
6. DQN
DQN 使用深度神经网络近似拟合状态动作值函数 Q ( s , a ) Q(s,a) Q(s,a).
-
上图就是一般的 Deep Q-network(DQN) 的算法。
-
初始化的时候,初始化 2 个网络:Q 和 Q ^ \hat{Q} Q^,一开始这个目标 Q 网络,跟原来的 Q 网络是一样的。在每一个 episode,你拿你的演员去跟环境做互动,在每一次互动的过程中,都会得到一个状态 s t s_t st,然后采取某一个动作 a t a_t at。怎么知道采取哪一个动作 a t a_t at 呢?就是根据现在的 Q-function。但是要有探索的机制。比如说用 Boltzmann 探索或是 Epsilon Greedy 的探索。那接下来得到奖励 r t r_t rt,然后跳到状态 s t + 1 s_{t+1} st+1。所以现在收集到一笔数据,这笔数据是 ( s t s_t st, a t a_t at , r t r_t rt, s t + 1 s_{t+1} st+1)。这笔数据放入 buffer 里面去。如果 buffer 满的话, 就再把一些旧的数据丢掉。接下来再从你的 buffer 里面去采样数据,那你采样到的是 ( s i , a i , r i , s i + 1 ) (s_{i}, a_{i}, r_{i}, s_{i+1}) (si,ai,ri,si+1)。这笔数据跟你刚放进去的不一定是同一笔,你可能抽到一个旧的。要注意的是,你采样出来的是一个 batch 的数据。接下来就是计算你的目标。假设采样出这么一笔数据。根据这笔数据去算你的目标。你的目标是什么呢?目标记得要用目标网络 Q ^ \hat{Q} Q^ 来算。目标是:
y = r i + max a Q ^ ( s i + 1 , a ) y=r_{i}+\max _{a} \hat{Q}\left(s_{i+1}, a\right) y=ri+amaxQ^(si+1,a) -
其中 a 就是让 Q ^ \hat{Q} Q^的值最大的 a。接下来我们要更新 Q 值,那就把它当作一个回归问题,希望 Q ( s i , a i ) Q(s_i,a_i) Q(si,ai) 跟你的目标越接近越好。然后假设已经更新了某一个数量的次,比如说 C 次,设 C = 100, 那你就把 Q ^ \hat{Q} Q^设成 Q,这就是 DQN。
6.1 DQN 和 Q-learning 有什么不同?
整体来说,DQN 与 Q-learning 的目标价值以及价值的更新方式都非常相似,主要的不同点在于:
- DQN 将 Q-learning 与深度学习结合,用深度网络来近似动作价值函数,而 Q-learning 则是采用表格存储;
- DQN 采用了经验回放的训练方法,从历史数据中随机采样,而 Q-learning 直接采用下一个状态的数据进行学习。
7. 练习
7.1 简答
- Target Network: 为了解决在基于TD的Network的问题时,优化目标 Q π ( s t , a t ) = r t + Q π ( s t + 1 , π ( s t + 1 ) ) \mathrm{Q}^{\pi}\left(s_{t}, a_{t}\right) =r_{t}+\mathrm{Q}^{\pi}\left(s_{t+1}, \pi\left(s_{t+1}\right)\right) Qπ(st,at)=rt+Qπ(st+1,π(st+1)) 左右两侧会同时变化使得训练过程不稳定,从而增大regression的难度。target network选择将上式的右部分即 r t + Q π ( s t + 1 , π ( s t + 1 ) ) r_{t}+\mathrm{Q}^{\pi}\left(s_{t+1}, \pi\left(s_{t+1}\right)\right) rt+Qπ(st+1,π(st+1))固定,通过改变上式左部分的network的参数,进行regression,这也是一个DQN中比较重要的tip
7.2 问答
1. 为什么在DQN中采用价值函数近似(Value Function Approximation)的表示方法?
答:首先DQN为基于深度学习的Q-learning算法,而在Q-learning中,我们使用表格来存储每一个state下action的reward,即我们前面所讲的状态-动作值函数 Q ( s , a ) Q(s,a) Q(s,a) 。但是在我们的实际任务中,状态量通常数量巨大并且在连续的任务中,会遇到维度灾难的问题,所以使用真正的Value Function通常是不切实际的,所以使用了价值函数近似(Value Function Approximation)的表示方法。
2. critic output通常与哪几个值直接相关?
答:critic output与state和actor有关。我们在讨论output时通常是对于一个actor下来衡量一个state的好坏,也就是state value本质上来说是依赖于actor。不同的actor在相同的state下也会有不同的output。
3. 我们通常怎么衡量state value function V π ( s ) V^{\pi}(s) Vπ(s)?分别的优势和劣势有哪些?
答:
- 基于Monte-Carlo(MC)的方法 :本质上就是让actor与environment做互动。critic根据”统计“的结果,将actor和state对应起来,即当actor如果看到某一state s a s_a sa ,将预测接下来的accumulated reward有多大如果它看到 state s b s_b sb,接下来accumulated reward 会有多大。 但是因为其普适性不好,其需要把所有的state都匹配到,如果我们我们是做一个简单的贪吃蛇游戏等state有限的问题,还可以进行。但是如果我们做的是一个图片型的任务,我们几乎不可能将所有的state(对应每一帧的图像)的都”记录“下来。总之,其不能对于未出现过的input state进行对应的value的输出。
- 基于MC的Network方法: 为了解决上面描述的Monte-Carlo(MC)方法的不足,我们将其中的state value function V π ( s ) V^{\pi}(s) Vπ(s) 定义为一个Network,其可以对于从未出现过的input state,根据network的泛化和拟合能力,也可以”估测“出一个value output。
- 基于Temporal-difference(时序差分)的Network方法,即TD based Network: 与我们再前4章介绍的MC与TD的区别一样,这里两者的区别也相同。在 MC based 的方法中,每次我们都要算 accumulated reward,也就是从某一个 state s a s_a sa 一直玩到游戏结束的时候,得到的所有 reward 的总和。所以要应用 MC based 方法时,我们必须至少把这个游戏玩到结束。但有些游戏非常的长,你要玩到游戏结束才能够 update network,花的时间太长了。因此我们会采用 TD based 的方法。TD based 的方法不需要把游戏玩到底,只要在游戏的某一个情况,某一个 state s t s_t st 的时候,采取 action a t a_t at 得到 reward r t r_t rt ,跳到 state s t + 1 s_{t+1} st+1,就可以应用 TD 的方法。公式与之前介绍的TD方法类似,即: V π ( s t ) = V π ( s t + 1 ) + r t V^{\pi}\left(s_{t}\right)=V^{\pi}\left(s_{t+1}\right)+r_{t} Vπ(st)=Vπ(st+1)+rt。
- 基于MC和基于TD的区别在于: MC本身具有很大的随机性,我们可以将其 G a G_a Ga 堪称一个random的变量,所以其最终的variance很大。而对于TD,其具有随机性的变量为 r r r ,因为计算 s t s_t st 我们采取同一个 action,你得到的 reward 也不一定是一样的,所以对于TD来说, r r r 是一个 random 变量。但是相对于MC的 G a G_a Ga的随机程度来说, r r r 的随机性非常小,这是因为本身 G a G_a Ga 就是由很多的 r r r 组合而成的。但另一个角度来说, 在TD中,我们的前提是 r t = V π ( s t + 1 ) − V π ( s t ) r_t=V^{\pi}\left(s_{t+1}\right)-V^{\pi}\left(s_{t}\right) rt=Vπ(st+1)−Vπ(st) ,但是我们通常无法保证 V π ( s t + 1 ) 、 V π ( s t ) V^{\pi}\left(s_{t+1}\right)、V^{\pi}\left(s_{t}\right) Vπ(st+1)、Vπ(st)计算的误差为零。所以当 V π ( s t + 1 ) 、 V π ( s t ) V^{\pi}\left(s_{t+1}\right)、V^{\pi}\left(s_{t}\right) Vπ(st+1)、Vπ(st)计算的不准确的话,那应用上式得到的结果,其实也会是不准的。所以 MC 跟 TD各有优劣。
- 目前, TD 的方法是比较常见的,MC 的方法其实是比较少用的。
4. 随机性策略和确定性策略有什么区别吗?
答:随机策略表示为某个状态下动作取值的分布,确定性策略在每个状态只有一个确定的动作可以选。 从熵的角度来说,确定性策略的熵为0,没有任何随机性。随机策略有利于我们进行适度的探索,确定 性策略的探索问题更为严峻。
5. 不打破数据相关性,神经网络的训练效果为什么就不好?
答:在神经网络中通常使用随机梯度下降法。随机的意思是我们随机选择一些样本来增量式的估计梯度,比如常用的 采用batch训练。如果样本是相关的,那就意味着前后两个batch的很可能也是相关的,那么估计的梯度也会呈现出某种相关性。不幸的情况下,后面的梯度估计可能会抵消掉前面的梯度量。从而使得训练难以收敛。