Matlab — 常见矩阵生成及矩阵运算

一、 常用矩阵生成

1. 零矩阵

A=zeros(N) %生成 NXN 的全零矩阵
A=zeros(M,N) %生成 M×N的全零矩阵
A=zeros(M,N,P,…) %生成 M×N×P 的全零矩阵
A=zeros(size(B)) %生成和矩阵 B 维数相同的全零矩阵

举例：

clc
clear all
A=zeros(5);%5阶0矩阵
A1=zeros(3,4);%3行4列
A2=zeros(3,4,3)
B=[1,2,3,4;5,6,7,8;10,11,12,13]
A3=zeros(size(B));

2. 单位矩阵

A=eye(N) %生成 NXN 的单位矩阵
A=eye(M, N) %生成 M×N 的单位矩阵，对角元素为 1，其余元素为 0
A=eye(size(B)) %生成和矩阵 B 维数相同的单位矩阵

举例：

clc
clear all
C=eye(5); %单位阵
C1=eye(3,4);
C3=eye(size(B));

3. 全1矩阵

A=ones(N)	%生成 N×N 的全 1 矩阵
A=ones(M,N) %生成 M×N 的全 1 矩阵
A=ones(M,N,P,…) %生成 M×N×P 的全 1 矩阵
A=ones(size(B)) %生成和矩阵 B 维数相同的全 1 矩阵

4. 幻方矩阵

M=magic(n) %生成 n 阶幻方矩阵，该矩阵由 1-n²之间任意整数构造而成且每行每列的和都相等
举例：

%幻方矩阵（一般可逆）
M=magic(3) %3x3的方阵，取值为1~n的平方,并进行排列，每一行、每一列的和相等

5. 随机整数排列

p=randperm(n) %生成正整数 1，2,…，n 的随机排列

举例：

clc
clear all
%随机整数排列（等步长）
p=randperm(10)  % 1~10的随机排列
p1=randperm(10)*0.1 % 0.1~1，步长为0.1的随机排列
p2=randperm(10-3+1)*10+20 %从30到100

6. 生成拓托普利兹矩阵

托普利兹矩阵简称 T 矩阵，其主对角线上元素相等，平行于主对角线的线上元素也相等。简单的 T 型矩阵包括前向位移矩阵和后向位移矩阵。

toeplitz(x,y) %生成一个以 x 为第一列，y 为第一行的托普利兹矩阵。

举例：

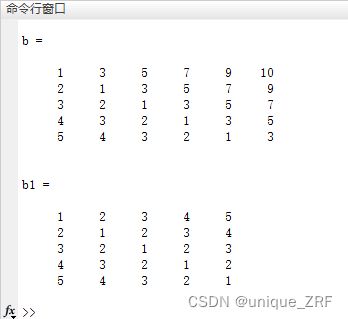
%托普里斯矩阵（对角线上元素相等）
c=[1 2 3 4 5]; %第一列的列向量
r=[1 3 5 7 9 10]; %第一行的行向量
b=toeplitz(c,r) %以c为第一列，r为第一行
b1=toeplitz(1:5) %生成方阵，第一列和第一行元素相同
%%若输入列的第一个元素与输入行的第一个元素不匹配。
         %在对角线冲突中，列具有更高优先级

7. 生成对角矩阵

A=diag(c) %生成由向量 c 中元素为对角线的对角矩阵
c=diag(A) %生成元素为矩阵 A 对角线元素的列向量
A=diag(c,k) %生成主对角线上第 k 条对角线元素为向量 c 的矩阵 A

举例：

e=diag(c); %以向量c为元素的对角阵
e1=diag(c,3); %第3条对角线的元素为c
e2=diag(1:6,2); %第2条对角线元素为1:6
e3=diag(1:7,1); %次对角线
e4=diag(1:8);
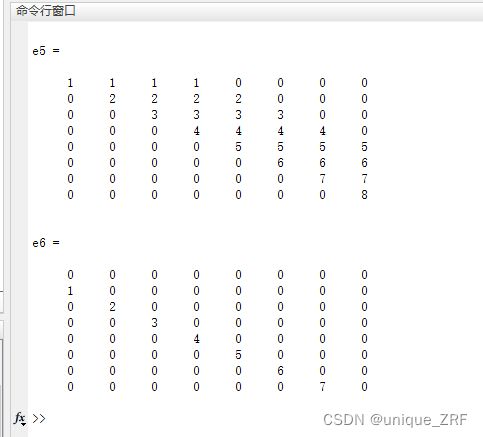
e5=e1+e2+e3+e4 %相加
e6=diag(1:7,-1) %下1个对角线的元素为1:7

8. 生成0-1均匀分布矩阵

A=rand(N) %生成大小为 N×N 的 0-1 之间均匀分布的随机数组
A=rand(M,N) %生成大小为 M×N 的 0-1 之间均匀分布的随机数组
A=rand(M,N,P,…) %生成大小为 M×N×P 的 0-1 之间均匀分布的随机数组
A=rand(size(B)) %生成和矩阵 B 维数相同的 0-1 之间均匀分布的随机矩阵

举例：

%均匀分布矩阵(取值范围为0~1之间)
f=rand(4) %4x4的均匀分布的矩阵
f1=rand(3,4)
f2=rand(size(f1)) %生成与f1大小相同的均匀分布矩阵
f3=rand(4)*10+10 %从10~20

9. 生成正态分布矩阵

A=randn(N) %生成大小为 N×N 的随机矩阵，其元素服从均值为 0，方差为1 的标准正态分布
A=randn(M, N) %生成大小为 M×N 的随机矩阵，其元素服从均值为 0，方差为1 的标准正态分布
A=randn(M,N,P,…) %生成大小为 M×N×P 的随机数组，其元素服从均值为 0，方差为 1 的标准正态分布
A=rand(size(B)) %生成和矩阵 B 维数相同的随机矩阵，其元素服从均值为 0，方差为 1 的标准正态分布

举例：

%正态分布矩阵(负无穷到正无穷)
%均值为0,方差为1
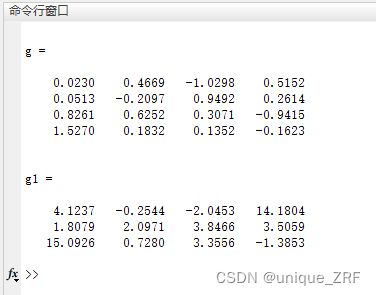
g=randn(4) %4阶矩阵
g1=randn(3,4)*6+5 %均值变为5，方差为6

二、矩阵运算

1. 行列式

d=det(A) %计算方阵 A 的行列式

举例：

clear all
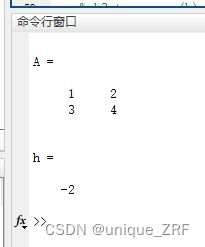
A=[1 2; 3 4]
det(A)

2. 矩阵转置

A’ %将矩阵 A 转置，若含有复数，则为共轭转置
A.’ %将矩阵 A 转置，若含有复数，转置后复数不变
transpose(A) %与 A.’功能相同

3. 矩阵尺寸改变

Y=reshape(X, m, n) %将矩阵 X 转换为 m×n 的二维矩阵 Y

举例：

% %矩阵转置
l=[1,2,3,4;5,0,17,8;9,10,11,12];
j=[1,3,5,2;3,3,2,5;3,4,6,8]
l1=l' %转置
k=l+j*i
k1=k' %共轭转置
k2=k.'%只转置不取共轭
k3=transpose(k) %转置
m=reshape(l,2,6) %l变为2*6的矩阵（矩阵顺序不变（按列排））
m2=reshape(l,size(j)) %变为3*4

4. 矩阵求和

Y=sum(X) %矩阵 X 各列元素的和所组成的向量
Y=sum(X,2) %矩阵 X 各行元素的和所组成的向量
Y=cumsum(X) %矩阵各列元素的和所组成的矩阵，Y(k,j)=sum(1:k,j)
Y=cumsum(X,2) %矩阵各行元素的和所组成的矩阵，Y(k,j)=sum(k,1:j)

举例：

 l=[1,2,3,4;5,0,17,8;9,10,11,12];
%矩阵求和
Y=sum(l) %列求和
Y1=sum(l,2) %行求和
Y2=cumsum(l) %第1行加到第2行，前两行加到第3行
Y3=cumsum(l,2)%第1列加到第2列，第1、2列加到第3列，前3列加到第4列

5. 矩阵求积

Y=prod(X) %矩阵 X 各列元素的积所组成的向量
Y=prod (X,2) %矩阵 X 各行元素的积所组成的向量
Y=cumprod(X) %矩阵各列元素的积所组成的矩阵，Y(k,j)=prod(1:k,j)
Y=cumprod(X,2) %矩阵各行元素的积所组成的矩阵，Y(k,j)=prod(k,1:j)

6. 矩阵元素查找

s=find(A) %查找矩阵 A 中的非零元素，返回这些元素的单下标
[m, n]=find(A) %查找矩阵 A 中的非零元素，返回这些元素的双下标

举例：

l=[1,2,3,4;5,0,17,8;9,10,11,12];
n=find(l) %矩阵l的所有非零的元素的位置(按列排)
n2=find(l>=10) %找l中大于等于10的元素的位置
[m8,n8]=find(l>=10) %找出大于等于10的元素的行号和列号
d8=l(m8,n8)
l(find(l>=10))=0 %把l中大于等于10的元素变为0

7. 矩阵的标准正交基、向量范数

B=orth(A) %矩阵B的列向量组成矩阵A的一组标准正交基，B’*B=eye(rank(A))
n=norm(X) %求向量/矩阵 X 的 2-范数（欧几里得范数）。
n=norm(X, 1) %求向量/矩阵 X 的 1-范数
n=norm(X, p) %求向量/矩阵 X 的 p-范数
n=norm(X, inf) %求向量/矩阵 X 的∞-范数

举例：

clc
clear all
%标准正交基
o=[1 0 4 6;0 -2 0 2;-1 -2 0 2]
q=orth(o') %列优先

%范数
O=o(1,:)%第一行
s=norm(O)%1范数
s1=norm(o,2)%2范数
s2=norm(o,inf) %无穷范数

8. 矩阵的迹、秩、特征值、特征向量、特征多项式

x=trace(A) %求矩阵 A 的迹
r=rank(A) %求矩阵 A 的秩

p=poly(A) %计算数值矩阵 A 的特征多项式 p
p=charpoly(A,v) %计算符号矩阵 A 的变量为 v 的特征多项式 p

e=eig(A) %求矩阵 A 的特征值
[C,D]=eig(A) %求矩阵 A 的特征向量和特征值

举例：

clc
clear all
%求迹/秩/特征值
M=magic(5)
R=rank(M)%求秩
t=trace(M)%求迹
E=eig(M)%求特征值
[D,E]=eig(M) %特征向量和特征值

%特征多项式
P=poly(M) %求出来为系数
syms v
P=charpoly(M,v) %特征多项式表达式