【深度学习_TensorFlow】手写数字识别

写在前面

到这里为止，我们已经学习完张量的常用操作方法，已具备实现大部分神经网络技术的基础储备了。这一章节我们将开启神经网络的学习，然而并不需要像学习前面那样了解大量的张量操作，而是将重点转向理解概念知识，到动手操作时，几行代码就能搞定。

手写数字识别作为入门级深度学习项目，因此本篇文章重点梳理代码流程，对于不成系统的知识点，我将放在本篇文章讲解，对于系统的知识点，我将其整理为单独的文章，这些文章为本篇文章服务，相信你能在读懂代码的同时，学会神经网络的新知识：

本篇文章的脉络，也是代码逻辑，更是你必须学会的重点：

• 学会下载、读取数据集

• 学会对数据类型转换和预处理

• 学会创建简单的神经网络

• 学会在网络内进行梯度求导、损失计算等操作

• 学会对训练模型的测试评估

---

写在中间

要想进行数字识别，我们当然得有相当多的手写数字来进行训练呀！实际上前人已经帮我们整理好了各式各样的数据，并将其汇总到不同的数据集之中，下面我们了解一下深度学习常用的数据集。

入门深度学习常用经典数据集

---

1. mnist 手写数字数据集：MNIST是一个手写数字数据集，包含60,000个训练图像和10,000个测试图像。每个图像都是28x28像素的灰度图像，其目标是识别图像中的数字。MNIST是深度学习领域最常用的数据集之一，因为它简单易懂，适合初学者入门。

2. CIFAR-10图像数据集：CIFAR-10是一个包含60,000张32x32像素彩色图像的数据集，每个图像都有10个类别的标签。CIFAR-10数据集是图像分类任务的经典数据集之一，也是深度学习领域广泛使用的数据集之一。

3. 波士顿住房数据集：是一个用于回归分析的经典数据集，它包含了506个样本和13个特征，目标是预测波士顿地区的房价。这个数据集广泛应用于机器学习和统计分析领域，可以用来训练和评估回归模型的性能。波士顿住房数据集的特点是数据量适中，特征维度较低，适合初学者入门。

4. ImageNet图像数据集：ImageNet是一个包含超过1400万张图像的数据集，涵盖了约22,000个类别。ImageNet数据集是计算机视觉领域最大、最复杂的数据集之一，也是深度学习领域广泛使用的数据集之一。

5. COCO物体检测数据集：COCO是一个用于物体检测和分割的数据集，包含超过30万张图像。COCO数据集是计算机视觉领域最广泛使用的数据集之一，也是深度学习领域物体检测和分割任务的经典数据集之一。

---

一、数据集读取与处理

数据集读取

---

了解完种类，那我们就拿一个简单的mnist数据集开刀，来看看这个数据集有什么特点，由于数据读取后自动转换为Numpy类型，我们就用Numpy的函数调用。

import keras.datasets.mnist
import tensorflow as tf

# 自动从网络下载 mnist 数据,并返回训练集和测试集的图像数据及对应标签。
# x 和 x_test 是训练集和测试集的图像数据,每个图像是28x28像素
# y 和 y_test 是训练集和测试集图像的标签,包含了每个图像对应的数字标签(0-9)
(x, y), (x_test, y_test) = keras.datasets.mnist.load_data()

print(x.shape)  # (60000, 28, 28)
print(y.shape)  # (60000,)
print(x.min(), x.max())  # 0 255

print(x_test.shape)  # (10000, 28, 28)
print(y_test.shape)  # (10000,)

# 数据集经过datasets函数，转换为Numpy类型
print(y[0:4])  # [5 0 4 1] 对训练集前四个标签切片

• load_data()函数返回两个元组(tuple)对象，第一个是训练集，第二个是测试集，每个 tuple 的第一个元素是多个训练图片数据，第二个元素是训练图片对应的类别数字。

• 其中训练集的大小为(60000,28,28)，代表了 60000 个样本，每个样本由 28 行、28 列构成，由于 是灰度图片，故没有 RGB 通道；训练集的大小为(60000)，代表了这 60000 个样本的标签数字，每个样本标签用一个范围为 0~9 的数字表示。

• 测试集 X 的大小为(10000,28,28)， 代表了 10000 张测试图片，测试集Y的大小为(10000)，代表了这10000个样本的标签数字0~9。

数据集简单处理

---

学会了读取数据集，下面对数据集进行简单处理，方便后面进行神经网络的搭建。

（ 1 ）对图像部分简单处理

对图像部分()的处理主要包括以下几个方面，我们逐一分析：

• 数据的随机打散

• 数据批训练

• 调用预处理函数调整数据类型

在这之前，我们得需要将原始的Numpy数据转换为Dataset 对象，才能利用TensorFlow 提供的各种便捷功能。

train_db = tf.data.Dataset.from_tensor_slices((x, y))  # 构建 Dataset 对象

接着就可以对数据进行逐步处理了。

• 数据的随机打散

在训练机器学习模型时，使用 Dataset.shuffle(buffer_size) 函数可以将数据样本随机打乱。这样可以防止每次训练时数据都按照固定的顺序产生，从而避免模型学习到过于相似的样本序列。增强模型的泛化能力，防止模型陷入“死记硬背”模式。

buffer_size 参数指定缓冲池的大小，一般设置为一个较大的常数即可

train_db = train_db.shuffle(10000)  # 随机打散样本，不会打乱样本与标签映射关系

• 数据的批训练

每一张图片的计算流程是通用的，但一张一张的处理这6万张图片未免有些太麻烦。我们在计算的过程中可以一次进行多张图片的计算，充分利用 CPU 或 GPU 的并行计算能力。

用形状为[ℎ, ]的矩阵来表示一张图片，对于多张图片来说，我们在前面添加一个数量维度(Dimension)，使用形状为[, ℎ, ]的张量来表示，其中代表了批量(Batch Size)；

通过 TensorFlow 的 Dataset 对象可以方便完成模型的批量训练，只需要调用 batch()函数即可构建带 batch 功能的数据集对象。其中 128为 Batch Size 参数，即一次并行计算 128个样本的数据。Batch Size 一般根据用户的 GPU 显存资源来设置，当显存不足时，可以适量减少 Batch Size 来减少算法的显存使用量。

train_db = train_db.batch(128) # 设置批训练，batch size 为 32

• 调用预处理函数调整数据类型

从 keras.datasets 中加载的数据集的格式大部分情况都不能直接满足模型的输入要求，因此需要自行实现预处理步骤。Dataset 对象通过提供 map(func)函数，可以非常方便地调用用户自定义的预处理逻辑，它实现在 func 函数里。例如，下方代码调用名为 preprocess 的函数完成每个样本的预处理：

train_db = train_db.map(preprocess) 

• 预处理函数

从 TensorFlow 中加载的 MNIST 数据图片，数值的范围为[0,255]。在机器学习中间， 一般希望数据的范围在 0 周围的小范围内分布。通过预处理步骤，我们把[0,255]像素范围 归一化(Normalize)到[0,1.]区间，或者缩放到[−1,1]区间，从而有利于模型的训练。

def preprocess(x, y): # 自定义的预处理函数 
# 调用此函数时会自动传入 x,y 对象，shape 为[b, 28, 28], [b]  

    x = tf.cast(x, dtype=tf.float32) / 255.     # 标准化到 0~1 
    x = tf.reshape(x, [-1, 28*28])     # 打平 
    y = tf.cast(y, dtype=tf.int32)    # 转成整型张量 
    y = tf.one_hot(y, depth=10)    # one-hot 编码 
    # 返回的 x,y 将替换传入的 x,y 参数，从而实现数据的预处理功能 
    return x,y  

为什么要将 MNIST 图片数据像素值范围从原始的[0,255]映射到 ∈ [0,1]或者[-1, 1]区间？（对于不同模型选择不同的映射范围可以参看《激活函数》这篇文章）

1. 数值稳定性：神经网络的训练过程中经常涉及到大量的数学运算。如果输入数据的范围过大或过分散，可能会导致计算结果出现严重的数值不稳定性。

2. 更快的收敛：将输入数据标准化到一个较小的范围，可以使得网络的权重和偏置在初始化时更接近于最优解，从而使网络更快地收敛。

3. 通俗解释： 想象一下你是一个教练，正在训练一个足球队。现在，你有两个选择：一个是在一个超级大的足球场上训练他们，另一个是在一个标准大小的足球场上训练他们。在超大的足球场上，球员们需要跑得更远，花费更多的时间，而且他们很难理解他们的位置在整个游戏中的重要性。但是，在标准大小的足球场上，球员们能更快地互相传递球，更好地理解他们在游戏中的位置，这会让训练更有效。

---

（ 2 ）对标签处理

对于标签的处理，我们通常放到上面的预处理函数( preprocess )中，但我们有必要单独拿出来说一说其中的one_hot()编码函数。

import keras.datasets.mnist
import tensorflow as tf

(x, y), (x_test, y_test) = keras.datasets.mnist.load_data()

print(y[0:4])  # [5 0 4 1] 对训练集前四个标签切片

# one-hot 编码是指只有一个位置为 1,其他位置为 0 的编码方式。它常用于分类任务中对标签的编码表示。
# 手写数字图片的总类别数有 10 种，所以深度depth就设为10
y_onehot = tf.one_hot(y, depth=10)
print(y_onehot[0:4])  # 输出训练集前三个onehot编码的图像数据，对应上面的[5 0 4 1]
# [[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
#  [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
#  [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
#  [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]]

为什么以及什么情况下要使用tf.one_hot()函数？

（猫、狗、马）可以用一个数字来表示标签信息，例如数字 0 表示猫，数字 2 表示马等 (编程实现时一般从 0开始编号)。但是数字编码一个最大的问题是，数字之间存在天然的大小关系，例如0 < 1 < 2，但它们类别之间并没有大小关系，所以采用数字编码的时候会迫使模型去学习这种不必要的约束。所以就需要新的表示方式。

在处理深度学习的多类别分类问题时，标签通常需要转换为one-hot编码。例如，有一个图像分类任务，需要将图像分类为3个类别（猫、狗、马），那么可以使用tf.one_hot()函数将每个类别的标签（0、1、2）转换为one-hot向量（
(1, 0, 0)，(0, 1, 0)，(0, 0, 1) ），和代码中的例子是相同的。

---

二、知识补充

上面的也许是开胃小菜，下面的部分可有些难度了，但我们不急着开始，先学习储备一些重要的知识。

网络构建

---

单层感知机或者简单的线性模型通常无法在 mnist 上取得很好的分类效果。需要使用多层神经网络才能学得较好的特征表示,从而对数据进行有效分类。

《感知机、全连接层、神经网络》 这篇文章讲解了网络构建的大体流程，我们可以简单了解。看完后你至少得学会两种网络构建方式。

前向传播与激活函数

---

学会了构建多层网络还不够，如果构建的网络模型是线性的，那处理像手写数字这样的分类问题还是很棘手的，需要将模型嵌套激活函数进行前向运算。

如果不了解激活函数的类型及使用，可以参看这篇文章《激活函数》

误差函数

---

接下来就是承上启下的误差函数了，它用来计算预测值和真实值之间的误差。对于损失函数的种类以及用法可以了解这篇文章《误差函数》。

梯度下降

---

最后就是将上一步计算出的误差从输出层反向传到输入层，这就是反向传播。在这个过程中，我们使用链式法则（Chain Rule）来计算每一层对误差的贡献，并据此更新每一层的权重和偏置，这就是所谓的梯度下降过程。

不理解梯度下降，可以参看这篇文章《梯度下降》

反向传播与链式法则部分讲解难度较大，且在tensorflow中有自动导函数，即使不理解原理也能轻松实现，我们以后再深入了解。

三、网络构建

下面我们开始配合代码进行流程讲解，def main()前的准备工作就是对数据集读取以及处理，之后就是代码的主体部分。以搭建一个三层的网络为开端：

1. 使用 TensorFlow 的 Sequential 容器可以非常方便地搭建多层的网络。对于 3 层网络，我们可以快速完成 3 层网络的搭建。由于网络层数不多，也可以手动创建三层网络。

model = keras.Sequential([ 
    layers.Dense(512, activation='relu'),
    layers.Dense(256, activation='relu'),
    layers.Dense(10)])

# 或者这样写

# 784 => 512
w1, b1 = tf.Variable(tf.random.truncated_normal([784, 512], stddev=0.1)), tf.Variable(tf.zeros([512]))
# 512 => 256
w2, b2 = tf.Variable(tf.random.truncated_normal([512, 256], stddev=0.1)), tf.Variable(tf.zeros([256]))
# 256 => 10
w3, b3 = tf.Variable(tf.random.truncated_normal([256, 10], stddev=0.1)), tf.Variable(tf.zeros([10]))

四、训练流程

创建完网络之后，训练流程如下：每次训练从 train_db 中取出一个批次的数据（for step, (x, y) in enumerate(train_db)），然后在此循环内计算该批次数据的损失函数，并计算损失函数关于各参数的梯度，并使用梯度下降法更新参数。每训练 100 个批次就输出一次损失函数的值。每训练 500 个批次就对测试集进行一次评估，计算分类准确率。

1. 数据迭代：使用for循环和enumerate函数，每一轮迭代都会从train_db数据集中取出下一个批次的数据（x，y）进行训练。

   for step, (x, y) in enumerate(train_db):
   

2. 自动求导：使用TensorFlow的GradientTape上下文管理器，在这个上下文中的运算步骤会被自动记录，以计算梯度。

   with tf.GradientTape() as tape:
   

3. 前向传播：进行神经网络的前向计算过程。这里的神经网络有三层，每一层先进行线性变换（x @ w + b），然后接ReLU激活函数。

   h1 = x @ w1 + b1
   h1 = tf.nn.relu(h1)
   h2 = h1 @ w2 + b2
   h2 = tf.nn.relu(h2)
   out = h2 @ w3 + b3
   

4. 计算损失：计算预测值与真实值之间的均方误差作为损失函数。

   loss = tf.reduce_mean(tf.square(y - out))
   

5. 计算梯度：在GradientTape的上下文中，使用gradient方法计算损失函数对所有参数（w1, b1, w2, b2, w3, b3）的梯度。

   grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
   

6. 更新参数：利用计算出的梯度，对每一个参数使用梯度下降法进行更新。lr是学习率。

   for p, g in zip([w1, b1, w2, b2, w3, b3], grads):
       p.assign_sub(lr * g)
   

7. 显示训练进度：每100步打印一次当前的损失值，以了解训练过程。

   if step % 100 == 0:
       print(step, 'loss:', float(loss))
   

至此模型的训练部分讲解完毕！

五、模型评估

我们把对数据集的所有样本迭代一遍叫作一个 Epoch，循环迭代多次后，可以在间隔数个 Epoch 后测试模型的准确率等指标，方便监控模型的训练效果。

在每500步训练后，对模型在测试集上的表现进行一次评估。

1. 评估标记：每500步训练后对模型进行一次评估。

   if step % 500 == 0:
   

2. 初始化统计量：初始化正确预测的数量total_correct和总预测数量total。

   total, total_correct = 0., 0
   

3. 数据迭代：使用for循环和enumerate函数，每一轮迭代都会从test_db数据集中取出一个批次的数据（x, y）进行评估。

   for step, (x, y) in enumerate(test_db):
   

4. 前向传播：进行神经网络的前向计算过程。这里的神经网络有三层，每一层先进行线性变换（x @ w + b），然后接ReLU激活函数。

   h1 = x @ w1 + b1
   h1 = tf.nn.relu(h1)
   h2 = h1 @ w2 + b2
   h2 = tf.nn.relu(h2)
   out = h2 @ w3 + b3
   

5. 预测和真实标签：对网络的输出out进行argmax操作，找出最大值的索引作为预测的类别，对真实标签y也做同样的操作，得到其类别。

   pred = tf.argmax(out, axis=1)
   y = tf.argmax(y, axis=1)
   

6. 计算正确数：使用tf.equal比较预测和真实标签是否相等，得到一个布尔值张量。然后将布尔值转化为整数，求和（tf.reduce_sum）得到这个批次的正确预测数量。

   correct = tf.equal(pred, y)
   total_correct += tf.reduce_sum(tf.cast(correct, dtype=tf.int32)).numpy()
   

7. 更新总数：将这个批次的样本数量加入到总数中。

   total += x.shape[0]
   

8. 计算并打印准确率：在完成所有测试数据的预测后，计算并打印模型的准确率。

   print(step, 'Evaluate Acc:', total_correct / total)
   

---

六、可视化结果

目前我们已经完成所有的关键代码，如何让代码锦上添花，将损失值和预测值可视化，就需要用一些绘图函数了。

要改动的地方实际上并不多：

1. 添加损失值：
   当每一步训练完成后，我们将步数（step）和对应的损失值（loss）以元组的形式添加到 losses 列表中。这样我们就可以追踪每一步的损失值。

2. 添加准确率：
   每当完成500步的训练，我们会在测试集上评估模型的准确率，并将步数（step）和对应的准确率值（acc）以元组的形式添加到 accuracies 列表中。这样我们就可以追踪训练过程中模型在测试集上的性能。

3. 绘制损失函数和准确率图：
   在训练完成后，我们使用 matplotlib 库来绘制两个图形：损失函数图和准确率图。这两个图分别显示了训练过程中的损失值和准确率的变化情况，以便于我们观察模型的训练进展。

   • 损失函数图：横轴是训练步骤，纵轴是损失值。图形应当显示出随着训练步骤的增加，损失值在逐渐减小，这表明模型在逐渐学习和拟合训练数据。

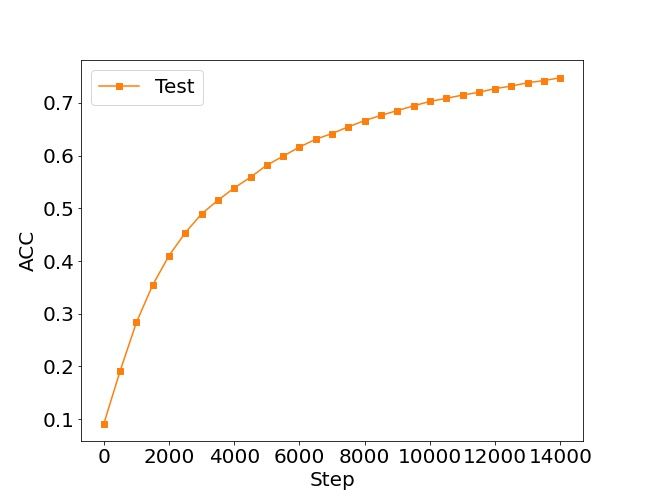
   • 准确率图：横轴是训练步骤（每500步一个数据点），纵轴是准确率。图形应当显示出随着训练步骤的增加，模型在测试集上的准确率在逐渐提高，这表明模型的泛化性能在提升。

import tensorflow as tf
from keras import datasets
import matplotlib.pyplot as plt

# 新增两个列表用于存储损失和准确率数据
losses = []
accuracies = []

# 省略了其它部分代码...

    # 可视化损失函数
    if step % 100 == 0:
        print(step, 'loss:', float(loss))
        losses.append(float(loss))

    # 评估数据
    if step % 500 == 0:
        total, total_correct = 0., 0

        for x, y in test_db:
            # 省略了其它部分代码...

        acc = total_correct / total
        print('Evaluate Acc:', acc)
        accuracies.append(acc)
# 绘制损失函数图
plt.figure()
x = [i*500 for i in range(len(losses))]
plt.plot(x, losses, color='C0', marker='s', label='Train')
plt.ylabel('MSE')
plt.xlabel('Step')
plt.legend()
plt.savefig('train.svg')

plt.figure()
x = [i*500 for i in range(len(accuracies))]
plt.plot(x, accuracies, color='C1', marker='s', label='Test')
plt.ylabel('ACC')
plt.xlabel('Step')
plt.legend()
plt.savefig('test.svg')
# 省略了其它部分代码...

if __name__ == '__main__':
    main()

最终效果如下：

写在最后

点赞，你的认可是我创作的动力！
⭐收藏，你的青睐是我努力的方向！
✏️评论，你的意见是我进步的财富！