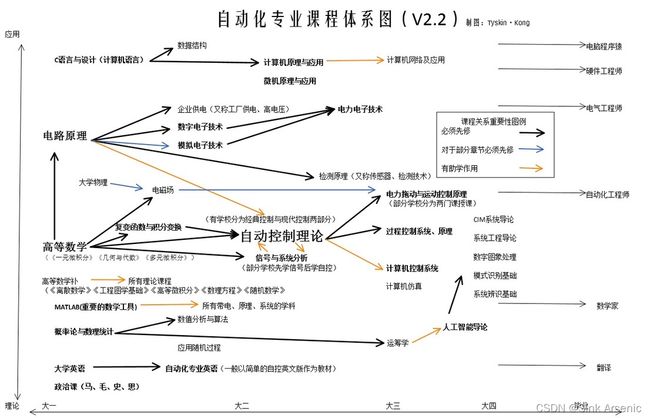
自动化专业本科学习笔记

可编程逻辑控制器 Programmable Logic Controller
数字电子技术
模拟电子技术
人工智能基础
微机原理与接口技术
最优控制与智能控制基础
数字信号处理
电子设计自动化
计算机控制系统
运动控制系统

自动控制原理

自动控制原理在生活中有哪些应用呢? - 王可的回答 - 知乎
https://www.zhihu.com/question/302141733/answer/531337039

搞懂 pid 概念

• 复习

零初始状态下，系统输出量的拉氏变换与输入量的拉氏变换之比为闭环系统的开环传递函数。零初始状态指输入作用在 t=0 之后才加到系统上，因此输入量及其各阶导数在 t=0-时为 0.输入作用之前是静止的所有 t=0-输出量及其各阶导数也为 0。

基本概念

自动控制：没有人直接参与的情况下，利用外加的设备或装置，使机器、设备、生产过程（即被控对象）的某个工作状态或参数（被控量）自动地按照预定的规律运行。

• 自动控制系统：
  • 给定环节：设定被控制量的给定量
    比较环节：所检测的被控量与给定量比较，确定偏差量
    校正环节
    放大环节：将信号放大成适合控制执行机构工作的信号
    执行机构：作用于控制对象，使被控量达到所要求的数值。
    被控对象
    反馈环节：检测装置（传感器）
• 闭环控制：系统的输出量经过测量变换后反馈到输入端，与给定信号相比较得偏差信号，偏差信号经由控制器作用使输出量按要求变化。
  • 作用：利用系统产生的偏差来控制和消除偏差，增加抗干扰能力和控制精度。
• 正反馈：提高系统放大系数，但容易使系统不稳定。
  • 例：在排尿反射过程中，当排尿中枢发动排尿后，由于尿液刺激了后尿道的感受器，后者不断发出反馈信息进一步加强排尿中枢的活动，使得排尿泛着一再加强，直至尿液排完为止。
  • 电子放大器线路中，利用正反馈可以提高放大器增益，提高放大器对频率的选择性，用来产生有用的周期性振荡信号。
• 负反馈：降低对系统前项通路元器件精度的要求。
• 开环控制系统：输入量→控制器→被控对象（扰动量）→输出量
  -----------------------------------------------
• 有静差系统（电机转速） 无静差系统（炮弹）

• “鲁棒性”，是指控制系统在一定（结构，大小）的参数摄动下，维持某些性能的特性。根据对性能的不同定义，可分为稳定鲁棒性和性能鲁棒性。以闭环系统的鲁棒性作为目标设计得到的固定控制器称为鲁棒控制器。

• 运算放大器是一个内含多级放大电路的电子集成电路，其输入级是差分放大电路，具有高输入电阻和抑制零点漂移能力；中间级主要进行电压放大，具有高电压放大倍数，一般由共射极放大电路构成；输出极与负载相连，具有带载能力强、低输出电阻特点。

• 反相器是可以将输入信号的相位反转180度，这种电路应用在模拟电路。

• 香农采样定理（又称奈奎斯特采样定理）

为了不失真地恢复模拟信号，采样频率应该不小于模拟信号频谱中最高频率的2倍。 　f s≥2f max

• 只有输入量对输出量产生顺向的控制作用：

  • 优点：结构简单，设计维护成本低。
  • 缺点：不具备抗干扰能力，因此在有扰动下达不到控制精度。

• 按干扰量补偿的开环控制系统

  • 利用可测量的扰动量，产生一种补偿作用，以减小或抵消扰动对输出量的影响。
  • 优点：在技术上比反馈控制简单，抗扰动性好，反应迅速。
  • 缺点：只能应用于扰动可测的场合，且一个补偿装置只能补偿一种扰动因素。

• 按输入量补偿的开环控制系统（前馈控制）

  • 系统给定经过一个前馈通道，叠加到系统的控制量上。
  • 优点：前馈校正通过提高开环增益，减小了稳态误差；从而提高了系统的控制精度，提高控制系统的响应速度。对于按扰动校正可在偏差产生前对系统进行校正。由于输入取自闭环外，故不影响系统的闭环特征方程式，即不影响系统的稳定性。
  • 缺点：不具备抗干扰能力，因此在有扰动下达不到控制精度。

• 复合控制系统：

  • 按偏差原则和按扰动补偿原则结合起来构成的系统。
  • 优点：控制作用迅速，控制精度更高。
  • 缺点：元件多，结构复杂

---

分析系统性能的方法

频率特性 ◀ ------- 微分方程 -------▶ 传递函数
频域 —傅氏变换 —时域— 拉氏变换 — 复域

• 线性系统
  • 时域分析：依据微分方程等数学模型求出系统的时间响应，由时间响应直接评价和分析系统的方法。
  • 根轨迹法：以某一变量为参变量，取值从 0 连续变化到无穷大是闭环特征根的轨迹。
  • 频域分析：依据系统的频率特性分析和设计
• 非线性系统
  • 等效线性化法
  • 相平面法
  • 李雅普诺夫稳定性分析
  • 计算机数值计算分析
  • 微分几何法
• 评判系统的性能指标 稳准快
  • 稳定性：稳定裕度
  • 稳态指标 （ 稳态误差 ）：开环对数幅频曲线的低频段
  • 暂态指标：对应中频段

时域分析

• 控制系统的输入变量变化后，输出变量随时间变化称为系统输出变量对输入变量的时间响应。
• 系统在典型信号作用下，输出量从初始状态到最终状态的时间相应过程称为暂态响应。
• 系统在典型信号作用下，时间趋于无穷时输出量的输出状态称为稳态响应。

暂态性能指标

• 最大超调量
  • 输出最大值与输出稳态值的相对误差
  • 反应系统的平稳性。最大超调量越小，系统过渡越平稳。允许误差带宽度一般取稳态输出值的 2%或5%
• 上升时间
  • 系统输出第一次达到输出稳态值所对应的时刻
  • 是系统响应速度的一种度量
• 调节时间（过渡过程时间）
  • 系统的输出量进入并一直保持在稳态输出值附近允许误差带内所需的时间。
  • 反应系统的快速性

频域

• 系统的频率响应：对于稳定的线性系统，当输入信号为正弦信号时，相同的稳态输出仍为同频率的正弦信号，只是幅值和相位发生了变化，这种过程称为频率响应。
• 频率特性：当输入信号为正弦函数时，频率特性是输出信号的傅氏变换与输入信号的傅氏变换之比称为频率特性。
  • 幅频特性：描述系统的稳态输出对于不同频率的正弦输入信号的衰减或放大的特性。
  • 相频特性：相位滞后或超前的特性。
  • 频率特性分析的特点：根据系统的频率特性能间接地揭示系统的动态性能和稳态性能，可以简单迅速地判断某些环节或者参数对系统的动态性能和稳态性能的影响，并能指明改进系统的方向。并且频率特性可以由实验确定，这在难以写出系统动态模型时更有用。
• 最小相位系统（minimum-phase system）：在一定的幅频特性情况下，其相移为最小的系统。对于闭环系统，开环零极点实部都大于等于0。（非最小：开环有，或有延迟环节）
• 稳态性能与 bode 图低频对应，暂态性能与中频段对应。

校正

• 目的：使系统有足够的稳定裕度，满意的动态响应，足够的增益使稳态误差达到规定要求。

非线性系统

• 非线性的特性：死区（不灵敏区）、饱和、间隙（回环）、摩擦、继电器特性。
• 改善非线性方法：改变线性部分的参数或对线性部分进行校正改变非线性特性；用震荡线性化改善系统性能。

描述函数法

• 描述函数：输入为正弦函数时，输出的基波分量与输入正弦量的复数比。
• 描述函数法实质：运用谐波线性化的方法，将非线性环节或系统的特性线性化，然后用线性系统频率特性分析法的结论去研究。（将非线性等效为线性，利用谐波线性化略去高次谐波。）
• 运用条件：可以化为典型结构，非线性部分输出中的高次谐波振幅小于基波振幅。且线性部分的低通滤波效应较好。

相平面

• 描述点：二阶系统用两个变量来描述相应的状态（相），在平面上可定出一个点，即描述点。
• 相轨迹：时间变化，状态相应变化，形成的一条轨迹为相平面，整个图形为相图。
• 条件：只适用于一阶与二阶。实质是将系统的运动过程形象的转化为相平面的一个点的移动，通过这个点的移动轨迹的研究来考察运动规律。
• 极限环：以系统的运动速度为纵坐标，以位移为横坐标的相平面上，振荡的相轨迹最终稳定在包围原点的一个圆圈上，称之为极限环。在非线性系统中，W(jw) = 负倒函数，则系统可能产生极限环振荡。
• 自振：没有外部激励条件下系统内部产生的稳定的周期运动。如果有一组参数（X,w）满足N(X)W(jw) = -1则系统处于临界稳定状态有的交点当系统周期运动的振幅稍有变化后，系统本身具有使振幅重新恢复原值的能力，则称周期运动是稳定的，称为自振。

离散

• 信号的采样：将模拟信号按一定时间采样成离散的模拟信号。对于惯性很大或者具有较大延迟特性的控制系统中，采样信号可以取得较好的控制效果。
• 采样定理: 从采样信号完全复现连续信号的条件是采样频率必须大于或等于输入采样开关的连续信号频谐中的最高频率的两倍。
• 保持器：把采样信号恢复为原来连续信号的过程。保持器的输出信号在每一个采样周期内的值为常数，其导数为零，称之为零阶保持器。它的作用是将采样值一直保持到下一个采样时刻，从而使采样信号变成阶梯信号。
• 脉冲传函：离散系统脉冲传递函数或z传递函数的定义为，输出脉冲序列的z 变换与输入脉沖序列的 z变换之比。
• 稳定条件：脉冲传函的全部极点位于z平面上以原点为圆心的单位圆内。否则将是不稳定的。

系统的数学模型：数学模型是用来描述系统因果关系的数学表达式。有微分方程、传递函数、结构图、信号流图、频率特性、差分方程等。

• 插值（过数据点）
• 拟合：最小二乘法
• 斐波那契数列
• 布雷斯悖论 减法反而提升效率
  

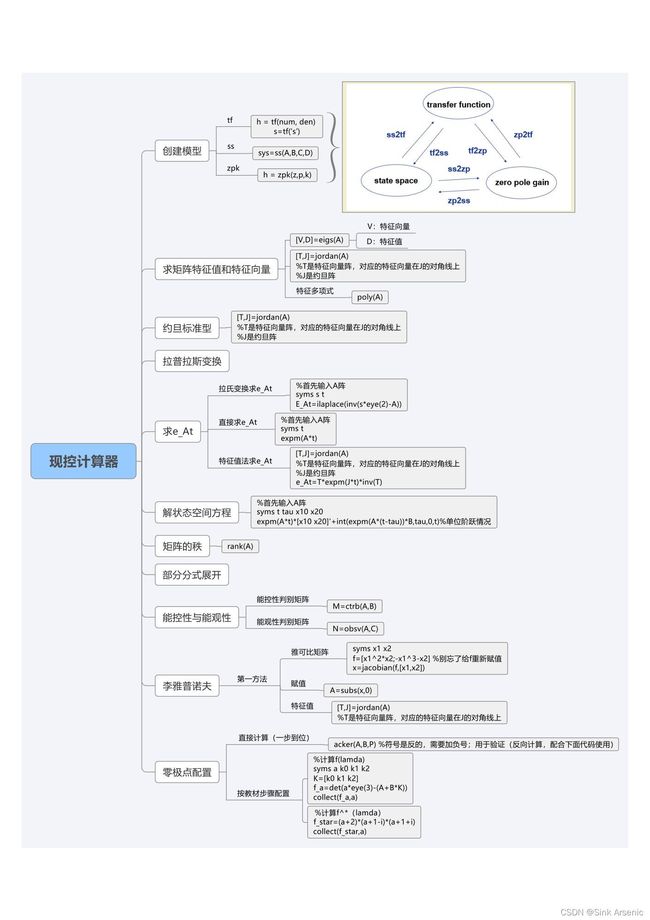
现代控制理论

• 状态空间基本概念
  所谓状态空间描述，就是用状态方程和输出方程来描述系统。
  状态方程描述了系统内部变量与外部控制作用的关系；
  输出方程描述了系统内部状态变量与输出变量之间的关系。
  状态空间描述从本质上揭示了系统输入输出关系与内部结构的内在联系，这为深入研究系统内部结构提供了可能性。
  状态变量的个数应该等于独立储能元件的个数。
  状态向量是线性无关的
  状态变量的可以任意多选，只要满足线性无关的

• 变换
  非奇异变换不改变系统的能控性（能观性）；
  只有系统完全能控（能观）才能通过非奇异变换化为能控（能观）标准型。

• 能控能观性
  对于SISO系统，系统能控能观的充要条件是：传递函数的分子分母间没有零极点对消。
  对MIMO系统，没有零极点对消只是最小实现的充分条件，而非必要条件，即使出现零极点对消，系统仍然可能是能控能观的。
  对于SISO系统，如果传递函数中出现了零极点对消，系统肯定不是能控且能观的，但是到底是不能控，还是不能观，或者是既不能控也不能观的，仍然不能确定。

• 对李雅谱诺夫函数的讨论
  V(x)是正定的标量函数，V(x)具有一阶连续偏导数；
  并不是对所有的系统都能找到V(x)来证明该系统稳定或者不稳定；
  V(x)如果能找到，一般是不唯一的，但关于稳定性的结论是一致的；
  V(x)最简单的形式是二次型；
  V(x)只是提供平衡点附近的运动情况，丝毫不能反映域外运动的任何信息；
  构造V(x) 需要一定的技巧。

• 定理

  • 1.5 状态向量的线性变换
    对于系统 ，若矩阵A具有n个两两相异的特征根 ，则存在线性非奇异变换将系统化为对角标准型

  • 3.2 线性定常系统的能控性能观性判别
    如果线性定常系统的系统矩阵A具有互不相同的特征值，则系统能控的充要条件是，系统经线性非奇异变换后，A阵变换成对角标准型，它的状态方程 B不包含元素全为0的行。

    若线性定常系统的系统矩阵具有重特征值，且对应于每一个重特征值只有一个约当块，则系统状态完全能控的充要条件是，经线性非奇异变换后，系统化为约当标准形。其中， B矩阵中与每个约当块最后一行相对应的那些行，其各行的元素不全为零。

    若A具有重特征值，若有重根对应一个以上的约旦块，则能控的充要条件是： B中与每个重根的约旦块最后一行对应的行均是行线性无关的。

    若线性定常系统的状态矩阵有互不相同的特征值，则系统状态能观测的充要条件是，经线性等价变换把矩阵化成对角标准形后，系统的状态空间表达式中，矩阵 Cˆ 不包含元素全为零的列。

    设线性定常系统的状态矩阵有不同的重特征值，且对应于每一重特征值只有一个约当块。则系统状态完全能观测的充要条件是，经线性等价变换将矩阵化成约当标准形后，系统的状态空间表达式。其中，与每个约当块第一列相对应的 矩阵的所有各列，其元素不全为零。

    若线性定常系统不完全能控且不完全能观，则存在线性变换，将状态空间可以化为将整个状态空间分解为能控能观、能控不能观、不能控能观、不能控不能观四个子空间。

    传递函数W(s)的一个实现为最小实现的充要条件是： 既是能控的又是能观的。

    设系统的状态方程为如果平衡状态 即， 如果存在标量函数V(x)满足：1） 对所有x具有一阶连续偏导数。2） 是正定的；3）若 是半负定的。则平衡状态 为在李亚普诺夫意义下的稳定。

    设系统的状态方程为如果平衡状态 即， 如果存在标量函数V(x)满足：1） 对所有x具有一阶连续偏导数。2） 是正定的；3）若 是负定的；或者 为半负定，对任意初始状态 ，除去x=0外，有 不恒为0。则平衡状态 是渐近稳定的。进一步当 ，有 ，则在原点处的平衡状态是大范围渐近稳定的。

    设系统的状态方程为如果平衡状态 即， 如果存在标量函数V(x)满足：1） 对所有x具有一阶连续偏导数。2） 是正定的；3）若 是正定的。则平衡状态 是不稳定的。

    平衡状态为大范围渐近稳定的充要条件是：对任意给定的正定实对称矩阵Q，必存在正定的实对称矩阵P，满足李雅普诺夫方程。

• 5.1 线性反馈控制系统的基本结构及其特性
  状态反馈不改变受控系统 的能控性，但不保证系统的能观性不变。
  输出反馈不改变系统的能控性和能观性。
  采用状态反馈对系统 任意配置极点的充要条件是系统 完全能控。
  对完全能控的单输入－单输出系统 ， 0 ( , , ) A b C不能采用输出线性反馈来实现系统极点的任意配置。
  对系统 采用从输出到 的线性反馈实现闭环极点任意配置的充要条件是：完全能观。
  对线性定常系统，状态观测器存在的充要条件是 的不能观子系统为渐近稳定。
  若线性定常系统完全能观，则其状态向量 x 可由输出 y 和输入 u 进行重构。

电力电子技术

三相半控桥 电阻时

串联二极管式电流型三相逆变器


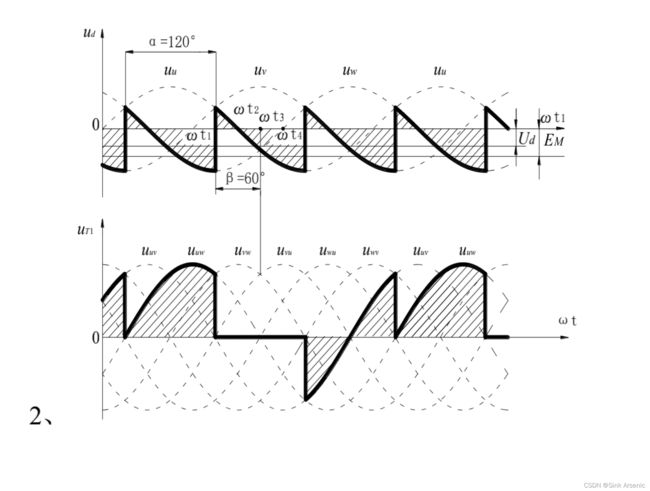
三相半波共阴极b=60 a=120

电压型三相逆变器

• 晶闸管串联时并联电阻和并联RC怎么就能起到均压作用?

  晶闸管由于批量生产不可能百每个都完全一致，这就会导致串联时两个管子不会同时导通而度是一个知先导通另一个会承受接近两倍的正向压降导道通，这可能会损伤器件。此时，并联电阻就是为了均压，即通版过并联后的等效压降接近来实现权同时导通以解决分压不均问题

第一象限是电动机运行，第二象限是发电机运行。第二象限时，转速为正，电磁转矩为负，表示电机转子从轴上吸收机械功率，电机变为发电机。当然此时电流也为负（相对于电动运行时），这也正是发电机的特点了。

• 对触发电路的要求
  触发电路输出的脉冲应具有足够大的功率；
  2）触发电路必须满足主电路的移相要求；
  3）触发电路必须与主电路保持同步。

电流型变频器的直流环节是电感器，而电压型变频器的直流环节是电容器。（3 分）
电压型变频器不能工作于再生制动状态，因为电容两端电压不能跃变。

• 提高变流装置的功率因数的常用方法有：
  减小触发角 增加整流相数 采用多组变流装置串联供电 设置补偿电容

• 两种电路的不同主要是： 有源逆变电路的交流侧接电网， 即交流侧接有电源。 而无源逆变电路的交流侧直接和负载联接。

• 逆变电路采用三相桥式结构。由于采用负载换流方式，故桥中开关元件可采用普通晶闸管。其出端A、B、C经限流电感Lа、Lb和Lc与公共电网联结。此处三相电网作为逆变电路负载接受其馈入电能，桥中各晶闸管T1～T6均工作于开关状态，采用相控方式（见电力电子电路）。各晶闸管的导通时刻由加到各门极脉冲的相位决定。逆变桥可视为按一定时序依次轮番通断的 6只开关。但在任何稳定导通状态中，桥中只有两支元件处于导通状态(其余为阻断状态)。例如在某一时刻有T1和T2导通，则有id=iA=-iC，即直流电流 id此时作为电网相电流iA和ic流向公共电网；而在另一时刻有T4和T5导通，则id=ic=-iA，由前述id为平滑连续直流电流。由于桥中各开关的轮番通断，iA和ic均为交变方波。同理可知iB也为交变方波。由此可见,若门极脉冲的基本重复频率保持与公共电网同步，则各相电流的重复频率也必然与电网同步，这样电网就得到由直流端提供的、由逆变电路转换的交流功率。
  　　当变换装置交流侧接在电网上，把直流电逆变成同频率的交流电回馈到电网上去，称为有源逆变。当变换装置交流侧和负载连接时，将由变换装置直接给电机等负载提供频率可变的交流电，这种工作模式称为无源逆变。

• 一般指电源的规格是交流输入直流输出，属于开关电源分类中的一种。AC/DC即为将交流变换为直流可调直流稳压电，其功率流向可以是双向的，功率流由电源流向负载的称为“整流”，功率流由负载返回电源的称为“有源逆变”。

• 有源逆变本质上是触发角大于90度的整流，有源逆变的拓扑结构与整流一模一样，只是当触发角大于90度时整流电路的功率方向发生了变化，相当于实现了逆变功能。所以有源逆变的交流侧一定需要电源。

• 在DCDC变换电路中不可以采用电网换流方法
  pwm脉宽调制型逆变电路中，采用不可控整流电源供电也能正常工作

• 晶闸管变流装置在主电路采用整流变压器降压后可以使晶闸管工作在一个合适的电压上，可以使晶闸管的电压定额下降，还可以使晶闸管工作于小控制角，这有利于减少波形系数，提高晶闸管的利用率，实际上也减少的晶闸管的电流定额，另外由于控制角小，这对变流装置的功率因素的提高也大为有利

面试

理解傅里叶

• The word control is usually taken to mean regulate，direct，or command. Control systems abound in our environment. In the most abstract sense it is possible to consider every physical object as a control system.

• In many cases，the design of control system is based on some theory rather than intuition or trail-and-error. Control theory is used for dealing with the dynamic response of a system to commands，regulations，or disturbances. The application of control theory has essentially two phases;dynamic analysis and control system design. The analysis pha-se is concerned with determination of the response of a plant (the controlled object) to commands，disturbances，and changes in the plant parameters. If the dynamic response is satisfactory，there need be no second phase. If the response is unsatisfactory and modification of the plant is unacceptable，a design phase is necessary to select the control elements (the controller) needed to improve the dynamic performance to acceptable levels.

• Control theory itself has two categories : classical and modern. Classical control theory ,which had its start during World War III，can be characterized by the transfer function concept with analysis and design principally in the Laplace and frequency domains. Modern control theory has arisen with the advent of high-speed digital computers and can be characterized by the state variable concept with emphasis on matrix algebra and with analysis and design principally in the time domain. As might be expected，each approach has its advantages and disadvantages as well as its proponents and detractors.

• As compared to modern approach，the classical approach has the tutorial advantage of placing less emphasis on mathematical techni-ques and more emphasis on physical understand-ing. Furthermore，in many design situations the classical approach is not only simpler but may be completely adequate. In those more complex cases where it is not adequate, the classical approach solution may aid in applying the modern approach and may provide a check on the more complete and exact design. For these reasons the subsequent articles will introduce the classical approach in detail.

翻译：

• “控制”一词通常用来指调节、指导或命令。控制系统在我们的环境中比比皆是。在最抽象的意义上，可以把每个物理对象看作一个控制系统。

• 在许多情况下，控制系统的设计是基于某种理论，而不是直觉或试错法。控制理论用于处理系统对命令、规则或干扰的动态响应。控制理论的应用本质上有两个阶段；动态分析和控制系统设计。分析阶段涉及确定设备(受控对象)对命令、干扰和设备参数变化的响应。如果动态响应令人满意，则不需要第二阶段。如果响应不令人满意，并且设备的修改不可接受，则需要设计阶段来选择将动态性能提高到可接受水平所需的控制元件(控制器)。

• 控制理论本身有古典和现代两大类。经典控制理论始于第三次世界大战，其特点是传递函数概念，主要在拉普拉斯和频域进行分析和设计。现代控制理论是随着高速数字计算机的出现而出现的，其特点是状态变量概念，强调矩阵代数，主要在时域进行分析和设计。不出所料，每种方法都有其优点和缺点，也有其支持者和反对者。

• 与现代方法相比，经典方法的教学优势在于不太强调数学技术，而更强调物理理解。此外，在许多设计情况下，经典方法不仅更简单，而且可能完全合适。在那些不够充分的更复杂的情况下，经典方法解决方案可能有助于应用现代方法，并可能对更完整和准确的设计进行检查。由于这些原因，后续文章将详细介绍经典方法。

拉普拉斯变换

• This definition of the transfer function requires the system to be linear and stationary，with continuous variables and with zero initial conditions. The transfer function is most useful when the system is also lumped parameter and when transport lags are absent or neglected. Under these conditions the transfer function itself can be expressed as a ratio of two polynomials in the complex Laplace.

• The Laplace transformation comes from the area of operational mathematics and is extremely useful in the analysis and design of linear systems. Ordinary differential equations with constant coefficients transform into algebraic equations that can be used to implement the transfer function concept. Furthermore，the Laplace domain is a nice place in which to work, and transfer functions may be easily manipulated，modified，and analyzed. The designer quickly becomes adept in relating changes in the Laplace domain to behavior in the time domain without actually having to solve the system equations. When time domain solutions are required， the Laplace transform method is straightforward. The solution is complete，including both the homogeneous (transient) and particular (steady-state) solutions，and initial conditions are automatically included. Finally ,it is easy to move from the Laplace domain into the frequency domain.

• 传递函数的这种定义要求系统是线性和平稳的，具有连续变量和零初始条件。当系统也是集总参数，并且没有或忽略传输滞后时，传递函数最有用。在这些条件下，传递函数本身可以表示为复数拉普拉斯中两个多项式的比值。

• 拉普拉斯变换来自运算数学领域，在线性系统的分析和设计中非常有用。常系数常微分方程转化为代数方程，可以用来实现传递函数的概念。此外，拉普拉斯域是一个很好的工作场所，传递函数可以很容易地操作、修改和分析。设计师很快就能熟练地将拉普拉斯域中的变化与时域中的行为联系起来，而无需实际求解系统方程。当需要时域解时，拉普拉斯变换方法很简单。解决方案是完整的，包括均匀(瞬态)和特定(稳态)解决方案，初始条件自动包括在内。最后，很容易从拉普拉斯域移到频域。