二叉搜索树(BST-Tree)(C++全)
目录
二叉搜索树基本概念
1,什么是根节点
2、什么是二叉搜索树
3、二叉搜索树结构
4、二叉搜索树的性质
5、复杂度
算法实现
1、创建一个二叉搜索树节点
2、打印二叉搜索树
3、二叉搜索树的插入
4、其他操作
(1)查找二叉搜索树的最大值
(2)查找二叉搜索树的最小值
(3)查找某一节点的前驱
(4)查找某一节点的后继
5、删除二叉搜索树的某一节点
步骤:
代码:
性能分析
二叉搜索树基本概念
1,什么是根节点
根结点(root)是树的一个组成部分,也叫树根。所有非空的二叉树中,都有且仅有一个根结点。简介,它是同一棵树中除本身外所有结点的祖先,没有父结点。
图中A就是根节点;
2、什么是二叉搜索树
二叉查找树(Binary SearchTree),(又: 二叉搜索树,二叉排序树)它或者是一棵空树, 或者是具有下列性质的二插树:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、 右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。
3、二叉搜索树结构
二叉搜索树是能够高效地进行如下操作的数据结构。
1.插入一个数值
2.查询是否包含某个数值
3.删除某个数值
4、二叉搜索树的性质
设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点,那么y.key≤x.key。如果y是x右子树中的一个结点,那么y.key≥x.key。
在二叉搜索树中:
1.若任意结点的左子树不空,则左子树上所有结点的值均不大于它的根结点的值。
2. 若任意结点的右子树不空,则右子树上所有结点的值均不小于它的根结点的值。
3.任意结点的左、右子树也分别为二叉搜索树。
5、复杂度
不论哪一种操作,所花的时间都和树的高度成正比。因此,如果共有n个元素,那么平均每次操作需要O(logn)的时间。
算法实现
1、创建一个二叉搜索树节点
一个二叉搜索树节点结构应该有{左孩子,右孩子,双亲}指针;
typedef int KeyType;
typedef struct BstNode
{
KeyType key;
BstNode* leftchild;
BstNode* rightchild;
BstNode* parent;
}BstNode,*BSTree;为了之后代码操作方便,提前写好购买节点的函数;
BstNode* Buynode()
{
BstNode* s = (BstNode*)malloc(sizeof(BstNode));
if (nullptr == s) exit(1);
memset(s, 0, sizeof(BstNode));
return s;
}
BstNode* MakeRoot(KeyType kx)
{
BstNode* s = Buynode();
s->key = kx;
return s;
}2、打印二叉搜索树
为了实验代码的演示结果;采用中序递归算法遍历;在二叉搜索树中中序遍历打印是按照从小到大的顺序打印;
其他几种遍历打印递归和非递归在我另一篇博客中:链接
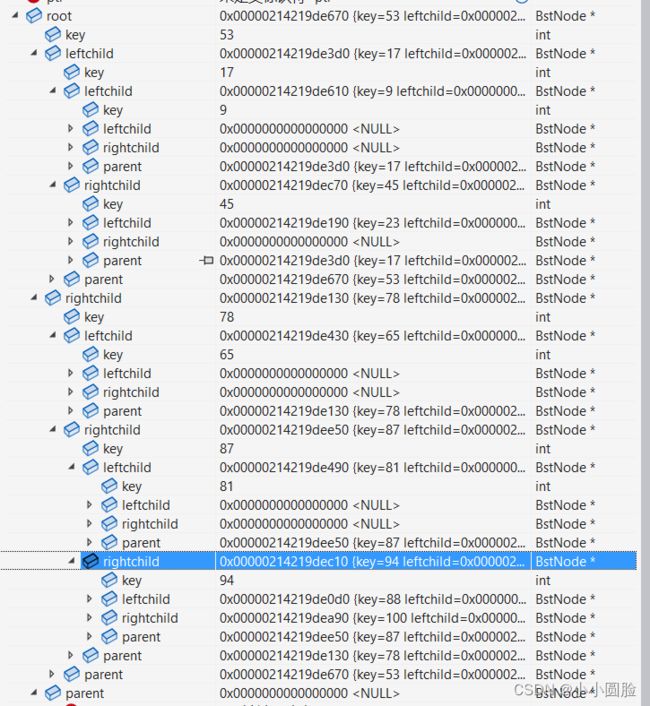
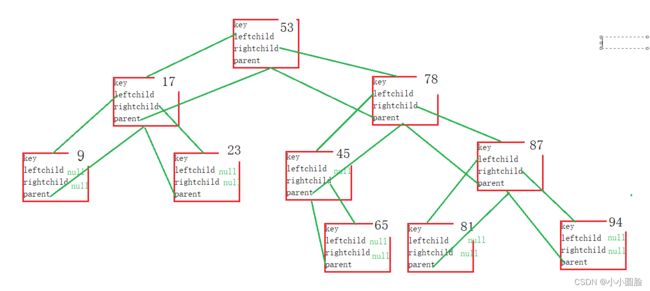
为了方便实验;采用统一的输入数据:int arr[] = { 53,17,78,9,45,65,87,23,81,94,88,100 };
代码:
void InOder(BstNode* ptr)
{
if (ptr != nullptr)
{
InOder(ptr->leftchild);
cout << ptr->key << " ";
InOder(ptr->rightchild);
}
}3、二叉搜索树的插入
步骤:(1)若根结点的关键字值等于查找的关键字,成功。
(2)否则,若小于根结点的关键字值,递归查左子树。
(3)若大于根结点的关键字值,递归查右子树。
(4)若子树为空,查找不成功
bool Insert(BstNode* &ptr, KeyType kx)
{
if (ptr == nullptr)
{
ptr = MakeRoot(kx);
return true;
}
BstNode* pa = nullptr;
BstNode* p = ptr;
while (p != nullptr && p->key != kx)
{
pa = p;
p = kx < p->key ? p->leftchild : p->rightchild;
}
if (p != nullptr && p->key == kx) return false;
p = Buynode();
p->key = kx;
p->parent = pa;
if (p->key < pa->key) { pa->leftchild = p; }
else { pa->rightchild = p; }
return true;
}4、其他操作
(1)查找二叉搜索树的最大值
BstNode* Last(BstNode* ptr)
{
while (ptr != nullptr && ptr->rightchild != nullptr)
{
ptr = ptr->rightchild;
}
return ptr;
}(2)查找二叉搜索树的最小值
BstNode* First(BstNode* ptr)
{
while (ptr!=nullptr&&ptr->leftchild!= nullptr)
{
ptr = ptr->leftchild;
}
return ptr;
}(3)查找某一节点的前驱
BstNode* Prev(BstNode* ptr)
{
if (ptr == nullptr) return nullptr;
if (ptr->leftchild != nullptr)
{
return Last(ptr->leftchild);
}
else
{
BstNode* pa = ptr->parent;
while (pa != nullptr && pa->rightchild != ptr)
{
ptr = pa;
pa = ptr->parent;
}
return pa;
}
}(4)查找某一节点的后继
BstNode* Next(BstNode* ptr)
{
if (ptr == nullptr)return nullptr;
if (ptr->rightchild != nullptr)
{
return First(ptr->rightchild);
}
else
{
BstNode* pa = ptr->parent;
while (pa != nullptr && pa->leftchild != ptr)
{
ptr = pa;
pa = ptr->parent;
}
return pa;
}
}5、删除二叉搜索树的某一节点
步骤:
1、若*p结点为叶子结点,即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构,则可以直接删除此子结点。
2、若*p结点只有左子树PL或右子树PR,此时只要令PL或PR直接成为其双亲结点*f的左子树(当*p是左子树)或右子树(当*p是右子树)即可,作此修改也不破坏二叉排序树的特性。
3、若*p结点的左子树和右子树均不空。在删去*p之后,为保持其它元素之间的相对位置不变,可按中序遍历保持有序进行调整,可以有两种做法:其一是令*p的左子树为*f的左/右(依*p是*f的左子树还是右子树而定)子树,*s为*p左子树的最右下的结点,而*p的右子树为*s的右子树;其二是令*p的直接前驱(或直接后继)替代*p,然后再从二叉排序树中删去它的直接前驱(或直接后继)-即让*f的左子树(如果有的话)成为*p左子树的最左下结点(如果有的话),再让*f成为*p的左右结点的父结点。在二叉排序树上删除一个结点的算法如下:
代码:
bool Remove(BstNode*& ptr, KeyType kx)
{
if (nullptr == ptr)return false;
BstNode* p = ptr;
while (p != nullptr && p->key != kx)
{
p = kx < p->key ? p->leftchild : p->rightchild;
}
if (p == nullptr)return false;
if (p->leftchild != nullptr && p->rightchild != nullptr)
{
BstNode* last = First(p->rightchild);
p->key = last->key;
p = last;
}
BstNode* pa = p->parent;
BstNode* child = p->leftchild != nullptr ? p->leftchild : p->rightchild;
if (child != nullptr) child->parent = pa;
if (pa == nullptr)
{
pa = child;
}
else
{
if (pa->leftchild == p)
{
pa->leftchild = child;
}
else
{
pa->rightchild = child;
}
}
free(p);
return true;
}性能分析
每个结点的C(i)为该结点的层次数。最坏情况下,当先后插入的关键字有序时,构成的二叉排序树蜕变为单支树,树的深度为其平均查找长度(n+1)/2(和顺序查找相同),最好的情况是二叉排序树的形态和折半查找的判定树相同,其平均查找长度和log 2 (n)成正比。
也就是说,最好情况下的算法时间复杂度为O(1),最坏情况下的算法时间复杂度为O(n)。