决策树(ID3、C4.5与CART)——从信息增益、信息增益率到基尼系数
目录
- 一、决策树
- 二、区别
- 三、ID3
-
- 1、信息熵与条件信息熵
- 2、信息增益(IG,information gain)
- 3、生成步骤
- 四、C4.5
-
- 1、信息增益率
- 2、连续特征
- 3、缺失值
- 4、正则化
- 5、总结
- 五、CART
-
- 1、简介
- 2、分类树
-
- 2.1、基尼指数
- 2.2、基尼指数与熵的关系
- 2.3、连续特征
- 2.4、离散特征
- 2.5、生成步骤:
- 3、回归树
-
- 3.1、方差
- 3.2、CART剪枝
一、决策树
- 决策树是分类算法,属于有监督学习。决策树的生成过程就是if-else的过程。
- 决策树的生成有两个要点:
1、节点特征的选择
2、节点分裂值的选择。
二、区别
1、ID3与C4.5采用信息熵作为选择准则的基础(ID3采用信息增益,C4.5采用信息增益率),CART选择基尼指数作为选择准则的基础(分类树采用基尼指数,回归树采用方差,用最小二乘法求解)。
2、ID3和C4.5只用于分类,CART可以用于分类与回归。其中I
3、ID3和C4.5可以是多叉树,CART是二叉树。
4、ID3只能使用离散特征,C4.5和CART可以处理连续特征。
5、ID3不能处理缺失值,C4.5可以处理缺失值。
三、ID3
ID3采用信息增益作为准则来划分属性。
1、信息熵与条件信息熵
信息熵(information entropy)用来衡量数据集的混乱程度(纯度),信息熵越大,则表明数据集的混乱程度越大。
数据集D的信息熵用如下公式表示,

其中,Ck表示属于第k类的个数,所有类别数量的总和为D的数量。

条件信息熵的公式如下:

2、信息增益(IG,information gain)
- 信息增益越大,则意味着采用该属性A划分节点获得的纯度提升更大。在每次划分中采用信息增益最大的划分。
- 信息增益偏好划分类别多的属性。例如某个属性是身份证号,则该属性每一个样本的值都不相同,条件信息熵为0,信息增益达到最大,但该属性的划分毫无意义,C4.5就是对划分准则的改进。
3、生成步骤
决策树的划分是一个递归过程。
(1)设置信息增益的阈值。
(2)选择信息增益最大的特征A。
(3)如果特征A的信息增益小于阈值A,则返回单节点树。采用投票法,该结点的类型为样本数量最多的类别。
(4)否则,按照特征A将节点划分为多棵子树,返回增加了子节点的节点。
(5)对各个子节点,递归调用上述步骤,直到达到停止标准(树的深度、信息增益阈值或者没有样本可划分)
四、C4.5
C4.5采用信息增益率作为划分标准。
1、信息增益率
信息增益率 = 信息增益 / 分裂熵
数据集D信息增益率的公式为:
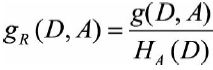
其中,分裂熵H(D)的公式为:

当A的取值越多时,分裂熵越大,信息增益率越小,达到了惩罚的目的。
需要注意的是,增益率可能会对数目少的特征有所偏好,因此C4.5采用了启发式的方法:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选出信息增益率最高的。
2、连续特征
C4.5采用二分法处理连续特征,将连续特征进行排列,将连续两个值的中间值作为分裂节点,将小于该值和大于该值的样本分为两个类别,找到信息增益最大的分裂点,本质上还是用的离散特征。
需注意的是,与离散属性不同,若当前节点划分属性为连续属性,该属性还可作为其后代节点的划分属性。
3、缺失值
(1)如何在属性值缺失的情况下划分属性
将数据集分成两部分:没有缺失值的部分、有缺失值的部分。对每个样本设置一个权重,将没有缺失值的部分按照占据总样本的比例计算信息增益率,并乘上所占比例。
(2)给定划分属性,若样本在该属性上缺失,如何对样本进行划分
若样本x在划分属性a上的取值未知,则将x同时划入所有子节点,且样本权值按所占比例和样本权值进行调整。直观地看,这就是让同一个样本以不同的概率划入到不同的子节点中。
4、正则化
C4.5引入了正则项进行了初步的过拟合处理。
5、总结
优点:
- 相比ID3,应用信息增益率进行特征选择
- 可以处理连续特征
- 可以处理缺失值
- 引入了正则化防止过拟合
缺点:
- 信息增益率采用熵的计算,里面有大量耗时的对数计算
- 多叉树的计算效率不如二叉树高
- 决策树模型容易过拟合,所以应该引入剪枝策略进行处理
五、CART
1、简介
CART的全称为Classification and Regression Tree,是最佳的决策树模型,sklear中的决策树也是应用的CART树。
CART是二叉树模型
2、分类树
2.1、基尼指数
分类树采用了基尼指数作为类别选择的依据。基尼纯度越小,代表数据集的纯度越高,分类效果越好。
特征p的基尼值公式如下:
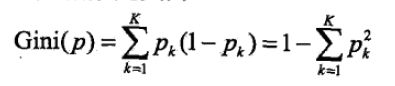
特别的,当特征只有两个类别时,基尼指数为:
![]()
对于特征A,若其将数据集分为D1和D2两部分,则其基尼指数为:
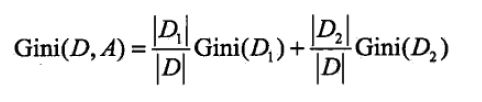
在候选集中,选择那个使得划分后基尼指数最小的属性作为最优的划分属性。
2.2、基尼指数与熵的关系
2.3、连续特征
与C4.5类似,采用连续特征离散化的思想。若特征A有k个取值,则有k-1个划分点,从这些划分点中选取基尼系数最小的划分点作为该特征的划分点。
2.4、离散特征
思想是将特征二分化,形成很多划分组合,在这些组合中找到基尼指数最小的作为特征的划分标准。
2.5、生成步骤:
CART树和ID3一样,也是递归的过程。给定阈值、树的深度作为输入的超参数。
1、如果基尼系数小于给定的阈值,则返回决策树子树,当前节点停止递归。如果当前节点的样本数小于阈值或者没有特征,返回决策子树,停止递归。
2、计算当前节点的现有的各个特征的各个特征值对数据集D的基尼系数。选择基尼系数最小的特征A和对应的特征值a。将数据集划分为两部分D1和D2。
3、对左右的子节点递归调用上述步骤。
对于生成的决策树预测时,加入测试集的样本X落到了某个叶子节点,而节点里有多个训练样本。则对于A的类别预测采用这个叶子节点里概率最大的类别。(所以也可以输出概率)
3、回归树
3.1、方差
回归树采用方差,利用最小二乘法求解方差和的极小值。
对于特征j,找到j所有的划分点s,s将数据集分为c1、c2两部分,找出使得两部分的方差最小,同时整体方差最小的特征j以及划分点s。

其中yi为数据集的均值:
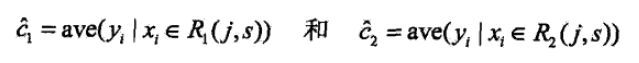
对于离散特征,采用均值或者中位数作为节点的输出结果。
3.2、CART剪枝
剪枝分为预剪枝和后剪枝,CART采用后剪枝。即先生成一颗决策树,然后产生所有剪枝后的CART树,使用交叉验证来检验各种减值后的效果,选择泛化能力最好的剪枝策略。
