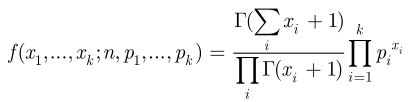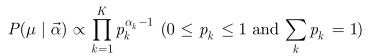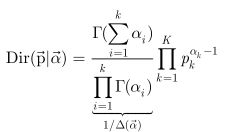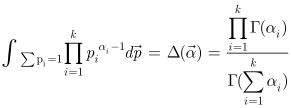主题模型LDA基础及公式推导

1.背景

(1)gamma函数产生

针对上述问题，欧拉将有限多项式的观察推广到无穷级数

欧拉发现了gamma函数性质

(2)LDA诞生

①blei以PLSA为基础，加上贝叶斯先验，诞生了LDA算法。LDA初始的论文使用变分EM方法训练（Variational Inference）。该方法较为复杂，而且最后训练出的 topic主题非全局最优分布，而是局部最优分布。后期发明了 Collapsed Gibbs Sampling 方法，推导和使用都较为简洁。

②Latent Dirichlet Allocation 是 Blei 等人于 2003 年提出的基于概率模型的主题模型算法，LDA 是一种无监督机器学习技术，可以用来识别大规模文档集或语料库中的潜在隐藏的主题信息。该方法假设每个词是由背后的一个潜在隐藏的主题中抽取出来。
对于语料库中的每篇文档，LDA 定义了如下生成过程（generative process）：

1. 对每一篇文档，从主题分布中抽取一个主题；
2. 从上述被抽到的主题所对应的单词分布中抽取一个单词；
3. 重复上述过程直至遍历文档中的每一个单词

LDA 认为每篇文章是由多个主题 mix 混合而成的，而每个主题可以由多个词
的概率表征。所以整个程序的输入和输出如下图所示：

代码参考：http://gibbslda.sourceforge.net/

2.基础知识

(1)gamma函数

类似于阶乘，但如果我们算0.5的阶乘，就需要用到gamma函数计算了。它的一般形式如下：

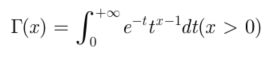
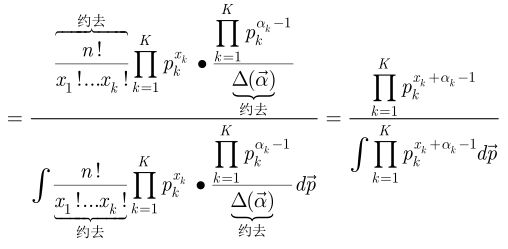
可以算出



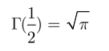
所以可以得到(以后看到这个公式就条件反射！)：

(2)二项分布(binomial distribution)

在每次试验中只有两 种可能的结果（成功/失败），每次成功的概率为 p，并且相互独立。这一系列试验总称为 n 重伯努利实验，当试验次数为 1 时，二项分布就是伯努利分布。

(3)beta分布

在概率论种，beta分布指一组定义在区间(0,1)的连续概率分布，有两个参数 α 和β ，且 α,β >0。
本质上，beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。(为主题出现概率的原理打下基础)

——参考：通俗理解beta分布(点击这里)

举例
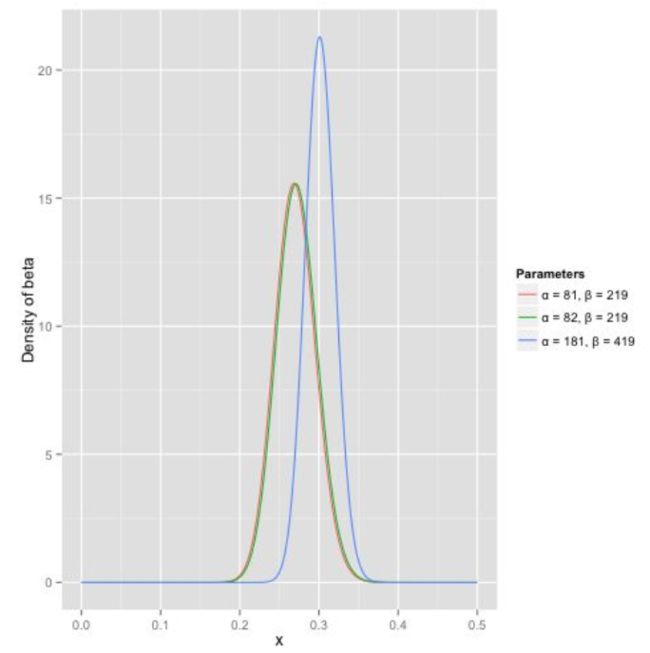
例如：要预测一个击球手击球概率， 就是用一个运动员击中的球数除以击球的总数。现在想预测他在某次赛季的击球率是多少？如果打了一次就命中了，难道击球率是100%，显然不合理。现在假设历史记录统计，他的击球率为0.27左右，它的命中范围在0.21到0.35之间，则由beta公式可以得到 α=81,β=219(见下图)

那么有了先验信息后，现在可以根据运动员本赛季的表现慢慢估测他在本赛季的击球率的概率分布了。
假设之前赛季是击中α0=81和遗漏β0=219(先验信息)，则加入下面公式更新Beta

现在本赛一共打了300次，其中击中了100次，200次没击中，则新分布为：

通过上述的例子，我们来证明Beta性质
①Beta分布的概率密度函数为：

其中称为β函数
②Beta与gamma函数关系
公式为(也称第一型欧拉积分)：

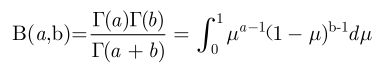
证明(有两种证明方法，这里使用分部积分法计算)：



通过递归，我们发现一个规律：

③Beta 分布的期望
后面Dirchlet分布也是同样的性质

(4)多项式分布(multinomial distribution)

①多项分布是二项分布的推广扩展，在 n 次独立试验中每次只输出 k 种结果
中的一个，且每种结果都有一个确定的概率 p。多项分布给出了在多种输出状态
的情况下，关于成功次数的各种组合的概率。

举个例子，投掷 n 次骰子，这个骰子共有 6 种结果输出（k=6），且 1 点出现概率为 p1 ，2 点出现概率 p2 ，…多项分布给出了在 n 次试验中，骰子 1 点出现 x1次，2 点出现 x2 次,3 点出现 x3 次，…，6 点出现 x6 次。
组合概率表示为：

也可以用gamma函数表示(和Dirichlet分布相似)

②多项分布的极大似然估计


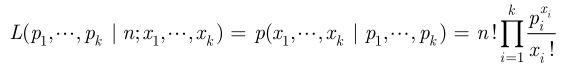
表达成 log-likelihood写法：

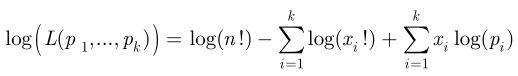
(5)狄利克雷分布(dirichlet distribution)

dirichlet 分布是 beta 分布在多项情况下的推广，也是多项分布的共轭先验分。
①概率密度如下

3.共轭先验分布

所谓的共轭，只是我们选取一个函数作为似然函数的 先验概率分布，使得后验分布函数和先验分布函数形式一致。比如 Beta 分布是二项式分布的共轭先验概率分布(之前棒球手例子，历史记录为二项式分布，即击中概率。后面的比赛记录会慢慢调整后验分布，这样也达到了共轭的目的)，而狄利克雷分布(Dirichlet 分布）是多项式分布的共轭先验概率分布。原因来源于贝叶斯估计：
后验分布=似然函数*先验分布

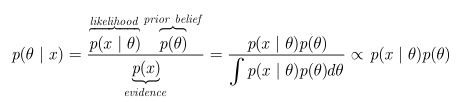
【参数估计】
Ⅰ.典型的离散型随机变量分布：二项式分布，多项式分布；
  典型的连续型随机变量分布：正态分布。他们都可以看着是参数分布，因为他们的函数形式都被一小部分的参数控制，比如正态分布的均值和方差，二项式分布事件发生的概率等。因此，给定一堆观测数据集（假定数据满足独立同分布），我们需要有一个解决方案来确定这些参数值的大小，以便能够利用分布模型来做密度估计。这就是参数估计！
Ⅱ.存在两个学派的不同解决方案。
  一是频率学派解决方案：通过某些优化准则（比如似然函数）来选择特定参数值；
  二是贝叶斯学派解决方案：假定参数服从一个先验分布，通过观测到的数据，使用贝叶斯理论计算对应的后验分布。先验和后验的选择满足共轭，这些分布都是指数簇分布的例子。

(1)从二项式到beta

①变换过程
  二项分布概率密度函数为：

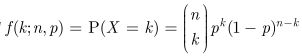
  将参数去掉，变成形式

再加上归一化因子 B(α,β)，转为beta分布(前一项β函数是确保 beta 分布是归一化)：

②证明
  二项分布的似然函数(这里s表示n次试验中成功的次数，f表示n 次伯努利试验中失败的次数。)

  先验分布 beta 分布如下

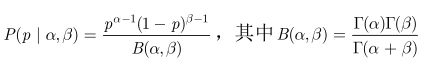
  由于先验分布*似然函数=后验分布

后验分布又变为 beta 分布，也就是和先验一致了，因此我们称之为共轭。同时 变成了

具体来讲，在某一个时间点，有一个观测值，此时可以得到后验，之后，每一个观测值的到来，都以之前的后验作为先验，乘以似然函数后，得到修正后的新后验。
另外，我们做先验分布的目的是估计参数，比如投掷硬币试验，我们需要根据已有的观测数据，估计下一次试验硬币的正面结果概率是多少。

(1)从多项式到Dirichlet分布

  ①多项式形式(先验)

这里代表这个分布的超参数(或伪计数)，

  加入归一化系数后，Dirichlet概率密度为：

②证明
  多项式分布似然函数

  先验分布Dirichlet

再根据后验=先验*似然函数

又因为：
，
用它替换掉分母可得：