K最近邻算法：简单高效的分类和回归方法（三）

引言

本节以KNN算法为主，简单介绍一下训练集和测试集、超参数

---

训练集和测试集

训练集和测试集是机器学习和深度学习中常用的概念。在模型训练过程中，通常将数据集划分为训练集和测试集，用于训练和评估模型的性能。

训练集是用于模型训练的数据集合。模型通过对训练集中的样本进行学习和参数调整来提高自身的预测能力。训练集应该尽可能包含各种不同的样本，以使模型能够学习到数据集中的模式和规律，并能够适应新的数据。

测试集是用于评估模型性能的数据集合。模型训练完成后，使用测试集中的样本进行预测，并与真实标签进行对比，以评估模型的精度、准确度和其他性能指标。测试集应该与训练集相互独立，以确保对模型的泛化能力进行准确评估。

一般来说，训练集和测试集的划分比例是80:20或者70:30。有时候还会引入验证集，用于在训练过程中调整模型的超参数。训练集、验证集和测试集是机器学习中常用的数据集拆分方式，以确保模型的准确性和泛化能力。

接下来我们回顾一下KNN算法的简单原理，选取离待预测最近的k个点，再使用投票进行预测结果

from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
from sklearn.datasets import load_iris  # 因为我们并没有数据集，所以从库里面调出来一个
iris = load_iris()
X = iris.data
y = iris.target
knn_clf.fit(X,y)
knn_clf.predict()

那么我们如何评价KNN模型的好坏呢？

这里我们将数据集分为两部分，一部分为训练集，一部分为测试集，因为这里的训练集和测试集都是有y的，所以我们只需要将训练集进行训练，然后产生的模型应用到测试集，再将预测的y和原本的y进行对比，这样就可以了

接下来进行简易代码演示讲解

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target

我们可以把y打印出来看看

这里我们不妨思考一下，如果训练集和测试集是8:2的话，测试集的y岂不是都是2了，那么还有啥子意义，所以我们需要将其打乱一下下，当然我们这里打乱的是index也就是下标，可不要自以为是的将y打乱了

import numpy as np
indexs = np.random.permutation(len(X))

导入必要的库后，我们将数据集下标进行打乱并保存于indexs中，接下来迎来重头戏分割数据集

test_ratio = 0.2
test_size = int(len(X) * test_ratio)
test_indexs = shuffle_indexs[:test_size] # 测试集
train_indexs = shuffle_indexs[test_size:] # 训练集

不信的小伙伴可以使用如下代码进行检验

test_indexs.shape
train_indexs.shape

接下来将打乱的下标进行分别赋值

X_train = X[train_indexs]
y_train = y[train_indexs]
X_test = X[test_indexs]
y_test = y[test_indexs]

分割好数据集后，我们就可以使用KNN算法进行预测了

from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_train)
y_predict = knn_clf.predict(X_test)

我们这里可以打印一下y_predict和y_test进行肉眼对比一下


最后一步就是将精度求出来

np.sum(np.array(y_predict == y_test,dtype='int'))/len(X_test)

---

sklearn中封装好的train_test_split

上面我们只是简单演示了一下，接下来我们使用官方的train_test_split

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y) # 注意这里返回四个结果

这里你可以试着看一眼，分割的比例与之前手动分割的比例大不相同
最后按部就班来就行

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_train)
knn_clf.predict(X_test) 
knn_clf.score(X_test,y_test)

---

超参数

什么是超参数，可以点击链接查看

在pycharm中我们可以查看一些参数

接下来通过简单的演示来介绍一下

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
knn_clf = KNeighborsClassifier(weights='distance') 
from sklearn.model_selection import train_test_split
iris = load_iris()
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y)

上面是老熟人了就不一一赘述了，但是注意这里面有个超参数（weights），这个参数有两种，一个是distance一个是uniform，前者和距离有关联，后者无关

---

首先测试一下n_neighbors这个参数代表的就行之前的那个k，邻近点的个数

%%time
best_k = 0
best_score = 0.0
best_clf = None
for k in range(1,21):
    knn_clf = KNeighborsClassifier(n_neighbors=k)
    knn_clf.fit(X_train,y_train)
    score = knn_clf.score(X_test,y_test)
    if score>best_score:
        best_score = score
        best_k = k
        best_clf = knn_clf
print(best_k)
print(best_score)
print(best_clf)

测试完参数n_neighbors，我们再来试试weights

%%time
best_k = 0
best_score = 0.0
best_clf = None
best_method = None
for weight in ['uniform','distance']:
    for k in range(1,21):
        knn_clf = KNeighborsClassifier(n_neighbors=k,weights=weight)
        knn_clf.fit(X_train,y_train)
        score = knn_clf.score(X_test,y_test)
        if score>best_score:
            best_score = score
            best_k = k
            best_clf = knn_clf
            best_method = weight
print(best_k)
print(best_score)
print(best_clf)
print(best_method)

最后我们测试一下参数p

%%time
best_k = 0
best_score = 0.0
best_clf = None
best_p = None
for p in range(1,6):
    for k in range(1,21):
        knn_clf = KNeighborsClassifier(n_neighbors=k,weights='distance',p=p)
        knn_clf.fit(X_train,y_train)
        score = knn_clf.score(X_test,y_test)
        if score>best_score:
            best_score = score
            best_k = k
            best_clf = knn_clf
            best_p = p
            
print(best_k)
print(best_score)
print(best_clf)
print(best_p)

或许大家不知道这个参数p的含义，下面我根据几个公式带大家简单了解一下

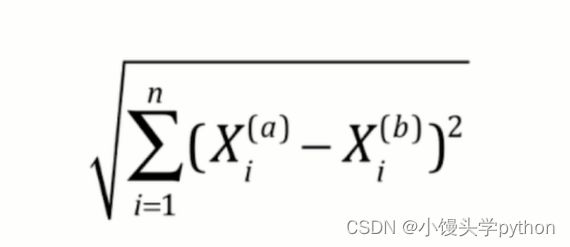
三张图分别代表欧拉距离、曼哈顿距离、明科夫斯基距离，细心的小伙伴就可以发现了，p=1位曼哈顿距离，p=2位欧拉距离，这里不做详细的说明，感兴趣的小伙伴可以翻阅相关数学书籍

挑战与创造都是很痛苦的，但是很充实。