七大查找算法（Java版）

  查找是在大量的信息中寻找一个特定的信息元素，查找的标准定义是：根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素（或记录）。
  从不同的方面来考虑，查找算法有不同的分类方式，以下为两种常见的分类方式：
   1>静态查找和动态查找

类别	特点
静态查找	只做查找操作的查找表，即：   1、查询某个“特定的”数据元素是否在表中   2、检索某个“特定的”数据元素和各种属性
动态查找	在查找中同时进行插入或删除等操作

   2>无序查找和有序查找

类别	特点
无序查找	被查找数列有序无序均可
有序查找	被查找数列为有序数列

  查找算法有七种，分别为：顺序查找、二分查找、插值查找、斐波那契查找、树表查找、分块查找、哈希查找。

一、顺序查找

1.1 顺序查找介绍

  顺序查找又称为线性查找，是一种最简单的查找方法。适用于线性表的顺序存储结构和链式存储结构。

• 基本思路
    从第一个元素m开始逐个与需要查找的元素x进行比较，当比较到元素值相同(即m=x)时返回元素m的下标，如果比较到最后都没有找到，则返回-1。
• 复杂度分析　
    查找成功时的平均查找长度为： ASL = 每个元素被查找的概率 * 总的元素的个数=1/n*(1+2+3+…+n) = (n+1)/2 ;
    当查找不成功时，需要n+1次比较，时间复杂度为O(n)，所以，顺序查找的时间复杂度为O(n)。
• 优缺点
    缺点：是当n 很大时，平均查找长度较大，效率低；
    优点：是对表中数据元素的存储没有要求。另外，对于线性链表，只能进行顺序查找。

1.2 顺序查找实现

  用Java代码实现顺序查找，示例代码如下：

	 private static int sequenceSearch(int[] array,int target){
		 for(int i=0;i<array.length;i++){
			 if(target==array[i])
				 return i;
		 }
		 return -1;
	 }

1.3 顺序查找优化

  在算法中，比较和赋值是比较耗时的。在上个章节的顺序查找实现代码中，存在着数组下标和目标值两种比较，那么能不能转变为一种比较呢？答案是可以的，不过要进行数据预处理，将查找值也放到数列中。比如将要查找的元素放在原数列中的第一位或最后一位(如果需要扩容就进行扩容)。此处将要查找的目标元素放在第一位，预处理示例代码如下：

		int[] array = {12,3,43,5,9};
		int target = 43;
		int[] newArray = new int[array.length+1];
		newArray[0] = target;
		for(int i=0;i<array.length;i++){
			newArray[i+1] = array[i];
		}

  也许有人会问，这样预处理一遍数据，需要将数组中所有数组都移动一遍，岂不是更花费时间？从总体上来看，确实是这样的。但是，面临大量的数据要处理时，常常要进行预处理、清洗等操作，这样会令纯粹处理数据（在该例子中就是搜索固定元素）的时间编的更少，更有效。当数据进行预处理后，搜索时就可以不用再比较两次，示例代码如下：

	public static int sequenceSearchPlus(int[] arr,int key){
		int n=arr.length-1;
		arr[0]=key;
		while(arr[n]!=key){
			n--;
		}
		return n;
	}

  完整的测试代码如下：

public class BasicTest {
	public static void main(String[] args){
		int[] array = {12,3,43,5,9};
		int target = 43;
		int[] newArray = new int[array.length+1];
		newArray[0] = target;
		for(int i=0;i<array.length;i++){
			newArray[i+1] = array[i];
		}
		int result = sequenceSearchPlus(newArray,target)-1;
		if(result != -1){
			System.out.println("要查找的元素,在数组中的下标是："+result);
		}else{
			System.out.println("要查找的元素不在数组中");
		}

	}	
	
	public static int sequenceSearchPlus(int[] arr,int key){
		int n=arr.length-1;
		arr[0]=key;
		while(arr[n]!=key){
			n--;
		}
		return n;
	}
}

  测试结果为：

要查找的元素,在数组中的下标是：2

二、二分查找

2.1 二分查找介绍

  二分查找，是一种在有序数组中查找某一特定元素的查找算法。

• 基本思路
    用给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。
• 复杂度分析　
    时间复杂度：折半搜索每次把搜索区域减少一半，时间复杂度为O(logn) 。
    空间复杂度：O(1)。
• 优缺点分析
    当查找表不会频繁有更新、删除操作时，使用折半查找是比较理想的。如果查找表有较频繁的更新、删除操作，维护表的有序会花费比较大的精力，不建议使用该查找方式。

2.2 折半查找实现

  用Java代码实现折半查找，有两种方式：迭代法和递归法，之前的文章已有提及，此处再写一下。迭代法示例代码如下：

	static  int binarySearch1(int arr[],int len,int target){
		/*初始化左右搜索边界*/
	    int left=0,right=len-1;
	    int mid;
	    while(left<=right){
	    	/*中间位置：两边界元素之和/2向下取整*/
	        mid=(left+right)/2;
	        /*arr[mid]大于target，即要寻找的元素在左半边，所以需要设定右边界为mid-1，搜索左半边*/
	        if(target<arr[mid]){
	            right=mid-1;
	        /*arr[mid]小于target，即要寻找的元素在右半边，所以需要设定左边界为mid+1，搜索右半边*/
            }else if(target>arr[mid]){
	            left=mid+1;
	        /*搜索到对应元素*/
	        }else if(target==arr[mid]){
	            return mid;
	        }
	    }
	    /*搜索不到返回-1*/
	    return -1;
	}

  递归法示例代码如下：

	static int binarySearch2(int array[],int left,int right,int target){
		if(left<=right){
			int mid=(left+right)/2;
			/*搜索到对应元素*/
			if(array[mid]==target){
				return mid;
			}else if(array[mid]<target){
				/*array[mid]小于target，即要寻找的元素在右半边，所以需要设定左边界为mid+1，搜索右半边*/
				return binarySearch2(array,mid+1,right,target);
			}else{
				/*array[mid]大于target，即要寻找的元素在左半边，所以需要设定右边界为mid-1，搜索左半边*/
				return binarySearch2(array,left,mid-1,target);
			}
		}else{
			return -1;
		}
	}

三、插值查找

3.1 插值查找介绍

  在二分查找中，每次都是从待查找序列的中间点开始查找，这样的做法在正确性上固然没什么问题，但假如要查找的值距离某个边界比较近，还从中间点开始查找，就有点浪费时间了。举个例子来说说明，假如在在一个{1,2…,100}的数组中，要查找88这个值，还一直采用和中间点比较的策略，就显得不太明智，因为明显可以明显从较为靠后的位置去检索。为了克服这种弊端， 引入了插值查找。

• 基本思路
    插值查找是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的 查找方法，其核心就在于插值的计算公式 (key-array[low])/(array[high]-array[low])*(high-low)。简而言之，基于二分查找算法，将查找点的选择改进为自适应选择。
• 复杂度分析　
    时间复杂性：如果元素均匀分布，则O(log(logn))，在最坏的情况下可能需要O(n)。
    空间复杂度：O(1)。
• 优缺点分析
    对于长度比较长、关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

3.2 插值查找实现

  上面的说法是总体介绍，落实到具体代码上的话，再慢慢分析。在二分查找中，mid的计算方式如下：
            
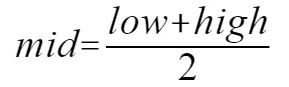
  将low从分数中提取出来，mid的计算就变成了：
            
  在插值查找中，mid的计算方式转换成了：
         
  有了上面的算术，就可以写代码了，迭代法插值查找示例代码如下：

	private static int insertSearch1(int arr[],int target){
		/*初始化左右搜索边界*/
	    int left=0,right=arr.length-1;
	    int mid;
	    while(left<=right){
	        mid=left+(target-arr[left])/(arr[right]-arr[left])*(right-left);
	        /*arr[mid]大于target，即要寻找的元素在左半边，所以需要设定右边界为mid-1，搜索左半边*/
	        if(target<arr[mid]){
	            right=mid-1;
	        /*arr[mid]小于target，即要寻找的元素在右半边，所以需要设定左边界为mid+1，搜索右半边*/
            }else if(target>arr[mid]){
	            left=mid+1;
	        /*搜索到对应元素*/
	        }else if(target==arr[mid]){
	            return mid;
	        }
	    }
	    /*搜索不到返回-1*/
	    return -1;
	}

  递归法插值查找示例代码如下：

	private static int insertSearch2(int array[],int left,int right,int target){
		if(left<=right){
			int mid=left+(target-array[left])/(array[right]-array[left])*(right-left);
			/*搜索到对应元素*/
			if(array[mid]==target){
				return mid;
			}else if(array[mid]<target){
				/*array[mid]小于target，即要寻找的元素在右半边，所以需要设定左边界为mid+1，搜索右半边*/
				return insertSearch2(array,mid+1,right,target);
			}else{
				/*array[mid]大于target，即要寻找的元素在左半边，所以需要设定右边界为mid-1，搜索左半边*/
				return insertSearch2(array,left,mid-1,target);
			}
		}else{
			return -1;
		}
	}

四、斐波那契查找

4.1 斐波那契查找介绍

  和前面的二分查找、插值查找相比，斐波那契查找是类似的，不过换了一种寻找mid点的方法。顾名思义，该种查找方法中，使用到了斐波那契数列，斐波那契数列的形式是：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）。

• 基本思路
    在斐波那契数列中的元素满足这样的关系：F[k]=F[k-1]+F[k-2]，此处将这个数组稍微改一下，改成：（F[k]-1）=（F[k-1]-1）+（F[k-2]-1）+1，图示如下：
      
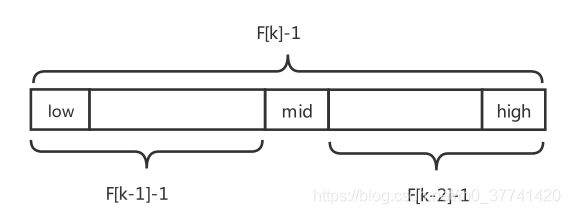
    通过上面的图，应该就可以看出为什么要这样分割数组了，因为要找出一个中间mid值，以便将数组按斐波那契数列的规律，分割成两部分。
• 复杂度分析
    最坏情况下，时间复杂度为O(logn)，且其期望复杂度也为O(logn)。

4.2 斐波那契查找实现

  上面介绍了分割的方法，但还有一个问题，就是斐波那契数列中的数值都是固定的，但要查找的数组的长度不固定，这样情况要怎么办？此时需要的是创建新数组，使新数组的长度是斐波那契数列中的值，并且是比原数组长度略大的值（此处只能是略大，因为略小的话，就会导致原数组元素丢失），多出来的元素用原数组最高位元素补充，示例代码如下：

		int high = arr.length - 1;
		int f[] = fib();
		/*获取最相邻的斐波那契数组中元素的值，该值略大于数组的长度*/
		while(high > f[k] - 1) {
			k++;
		}
		/*因为 f[k]值可能大于arr的长度。如果大于时，需要构造一个新的数组temp[]，将arr数组中的元素拷贝过去，不足的部分会使用0填充*/
		int[] temp=Arrays.copyOf(arr, f[k]);
		/*然后将temp后面填充的0，替换为最后一位数字
		 *如将temp数组由{1,8,10,89,100,134,0,0}变换为{1,8,10,89,100,134,134,134}*/
		for(int i = high + 1; i < temp.length; i++) {
			temp[i] = arr[high];
		}

  解决了如何分割、如果创建临时新数组后，还有一个问题：怎么判断最后target == arr[i]时，这个arr[i]是原来的数组中的元素，还是在新数组中扩展出来的元素？如果是新数组中扩展出来的元素，该元素的下标是大于原数组元素的最大下标的，肯定不是要寻找的位置。其实该问题容易解决，就是当target == arr[i]时，如果arr[i]的下标>原数组最大下标时，直接返回元数组最大下标即可。示例代码如下：

				/*原arr数组中的值*/
				if(mid <= high){
					return mid;
				/*在temp中，扩展出来的高位的值*/
				}else{
					return high;
				}

  完整斐波那契查找示例代码如下：

public class FibonacciSearch {
	
	public static int FLENGTH = 20;
	public static void main(String[] args) {
		int [] arr = {1,8,10,89,100,134};
		int target = 89;
		System.out.println("目标元素在数组中位置是：" + fibSearch(arr, target));		
	}

	public static int[] fib() {
		int[] f = new int[FLENGTH];
		f[0] = 1;
		f[1] = 1;
		for (int i = 2; i < FLENGTH; i++) {
			f[i] = f[i-1] + f[i-2];
		}
		return f;
	}
	
	public static int fibSearch(int[] arr, int target) {
		int low = 0;
		int high = arr.length - 1;
		int k = 0; 
		int mid = 0; 
		int f[] = fib();
		/*获取最相邻的斐波那契数组中元素的值，该值略大于数组的长度*/
		while(high > f[k] - 1) {
			k++;
		}
		/*因为 f[k]值可能大于arr的长度。如果大于时，需要构造一个新的数组temp[]，将arr数组中的元素拷贝过去，不足的部分会使用0填充*/
		int[] temp=Arrays.copyOf(arr, f[k]);
		/*然后将temp后面填充的0，替换为最后一位数字
		 *如将temp数组由{1,8,10,89,100,134,0,0}变换为{1,8,10,89,100,134,134,134}*/
		for(int i = high + 1; i < temp.length; i++) {
			temp[i] = arr[high];
		}
		
		while (low <= high) { 
			mid = low + f[k - 1] - 1;
			if(target < temp[mid]) { 
				high = mid - 1;
				/*因为f[k]=f[k-1]+f[k-2]，所以k--就相当于取temp数组的左边部分*/
				k--;
			} else if ( target > temp[mid]) { 
				low = mid + 1;
				/*同理，f[k]=f[k-1]+f[k-2]，k -= 2就相当于取temp数组的右边部分*/
				k -= 2;
			} else {
				/*原arr数组中的值*/
				if(mid <= high){
					return mid;
				/*在temp中，扩展出来的高位的值*/
				}else{
					return high;
				}
			}
		}
		return -1;
	}
}

五、树表查找

5.1 二叉树查找介绍

  二叉排序树是最简单的树表查找算法，该算法需要利用待查找的数据，进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，然后再进行查找。

5.1.1 二叉排序树性质

  二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
   1>若左子树不空，则左子树上所有结点的键值均小于或等于它的根结点的键值。
   2>若右子树不空，则右子树上所有结点的键值均大于或等于它的根结点的键值。
   3>左、右子树也分别为二叉排序树。

5.1.2 二叉排序树中序遍历

  二叉排序树有不同的遍历方式，中序遍历的结果比较直观，是一个有序的序列。二叉树示例如下：
          
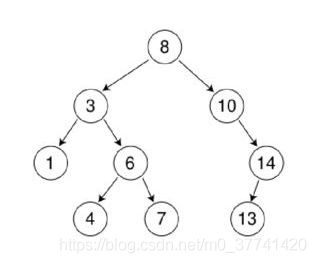
  二叉树上中序遍历的方式是：左节点、当前节点、右节点。该二叉树的遍历结果为：1、3、4、6、7、8、10、13、14。

5.1.3 二叉树查找步骤

  先创建二叉排序树，再进行查找。

5.2 二叉树查找实现

  首先，要创建一个树的节点，节点中要有该节点储存的值，然后起左右子树。示例代码如下：

class BinaryTree{
    int value;
    BinaryTree left;
    BinaryTree right;
    public BinaryTree(int value){
        this.value = value;
    }
}

  接下来就要创建二叉排序树，创建二叉排序树是一个递归的过程，需要将序列中的值一个一个添加到二叉树中。方便起见，可以利用序列中第一个元素作为根节点，再持续添加节点，示例代码如下：

        int[] array = {35,76,6,22,16,49,49,98,46,9,40};
        BinaryTree root = new BinaryTree(array[0]);
        for(int i = 1; i < array.length; i++){
            createBST(root, array[i]);
        }

  具体创建树的过程，就是一个不断与根节点比较，然后添加到左侧、右侧或不添加的过程。也许有人会有疑问，为什么会存在不添加的情况？因为在二叉排序树中，不存在重复元素，有相等元素已经在树中时，直接忽略后续相等元素。示例代码如下：

    public static void createBST(BinaryTree root, int element){
        BinaryTree newNode = new BinaryTree(element);
        if(element > root.value){
            if(root.right == null)
                root.right = newNode;
            else
                createBST(root.right, element);
        }else if(element < root.value){
            if(root.left == null)
                root.left = newNode;
            else
                createBST(root.left, element);
        }else{
            System.out.println("该节点" + element + "已存在");
            return;
        }
    }

  查找元素是否在树中的过程，就是一个二分查找的过程，不过查找的对象从左右子序列转换成了左右子树而已。示例代码如下：

    public static void searchBST(BinaryTree root, int target, BinaryTree p){
        if(root == null){
            System.out.println("查找"+target+"失败");
        }else if(root.value == target){
            System.out.println("查找"+target+"成功");
        }else if(root.value >= target){
            searchBST(root.left, target, root);
        }else{ 
            searchBST(root.right, target, root);
        }
    }

  完整示例代码如下：

public class BinarySortTree {
    
    public static void main(String[] args) {
        int[] array = {35,76,6,22,16,49,49,98,46,9,40};
        BinaryTree root = new BinaryTree(array[0]);
        for(int i = 1; i < array.length; i++){
            createBST(root, array[i]);
        }
        System.out.println("中序遍历结果：");
        midOrderPrint(root);
        System.out.println();
        searchBST(root, 22, null);
        searchBST(root, 100, null);
    }
    
    /*创建二叉排序树*/
    public static void createBST(BinaryTree root, int element){
        BinaryTree newNode = new BinaryTree(element);
        if(element > root.value){
            if(root.right == null)
                root.right = newNode;
            else
                createBST(root.right, element);
        }else if(element < root.value){
            if(root.left == null)
                root.left = newNode;
            else
                createBST(root.left, element);
        }else{
            System.out.println("该节点" + element + "已存在");
            return;
        }
    }
    
    /*二叉树中查找元素*/
    public static void searchBST(BinaryTree root, int target, BinaryTree p){
        if(root == null){
            System.out.println("查找"+target+"失败");
        }else if(root.value == target){
            System.out.println("查找"+target+"成功");
        }else if(root.value >= target){
            searchBST(root.left, target, root);
        }else{ 
            searchBST(root.right, target, root);
        }
    }
    
    /*二叉树的中序遍历*/
    public static void midOrderPrint(BinaryTree rt){
        if(rt != null){
        	midOrderPrint(rt.left);
            System.out.print(rt.value + " ");
            midOrderPrint(rt.right);	
        }
    }
}

  测试结果为：

该节点49已存在
中序遍历结果：
6 9 16 22 35 40 46 49 76 98
查找22成功
查找100失败

六、分块查找

6.1 分块查找介绍

  分块查找，顾名思义，要先将所有元素按大小进行分块，然后在块内进行查找。在分块时，块内的元素不一定是有序的，只要一个块内的元素在同一区间就行。用较标准的语言描述是：算法的思想是将n个数据元素"按块有序"划分为m块（m≤n）。每一块中的结点不必有序，但块与块之间必须"按块有序"，每个块内的的最大元素小于下一块所有元素的任意一个值。
  所以，在使用分块查找时，分成了两步：
   1>找到元素可能在的块。
   2>在对应的块内查找元素。

6.2 分块查找实现

  在上个章节说到，该方法要先分块，那么块应该具有怎样的属性呢？至少要有以下元素：
   1>长度
    一般是固定的长度。
   2>起始位置
    当块的长度固定后，需要确定起始位置才能固定不同的块表示的元素的位置范围。
   3>块标识
    该标识用来标识块内元素的范围，可以用最大值、最小值、平均值等多种方式来表示。
  示例代码如下：

public class Block {
	/*block的索引，用来标识块中元素*/
    public int index;
    /*该block的开始位置*/
    public int start; 
    /*块元素长度，在该例子中0代表空元素，不计入block长度*/
    public int length;
	
    public Block(int index, int start, int length) {
        this.index = index;
        this.start = start;
        this.length = length;
    }
}

  在该例子中，定义元素数组和块数组，示例如下：

	/*主表*/
    static int[] valueList = new int[]{
    	104, 101, 103, 105,102, 0, 0, 0, 0, 0,
        201, 202, 204, 203,0,   0, 0, 0, 0, 0,
        303, 301, 302,  0,   0,   0, 0, 0, 0, 0
    };

    /*索引表*/
    static Block[] indexList = new Block[]{
    	new Block(1, 0, 5),
    	new Block(2, 10, 4),
    	new Block(3, 20, 3)
    };

  valueList中的0，可以简单理解为块内的空元素；indexList中的1,2,3代表块内元素的取值范围，第一个块内是100-200之间的元素，第2个块内是200-300之间的元素，以此类推。
  在进行元素查找时，先判断是否存在元素可能存在的块。示例如下：

	    /*确定插入到哪个块中，在该例子中，第一个block中放的是100-200之间的数，第二个block中放的是200-300之间的数，以此类推*/
	    int index = key/100;
	    /*找到对应的block*/
	    for(int i = 0;i < indexList.length; i++) {
	       if(indexList[i].index == index) {
	           indexItem = indexList[i];
	           break;
	       }
	   }

	    /*如果数组中不存在对应的块，则返回-1，查找失败*/
	   if(indexItem == null)
	       return -1;

  找到内对的块后，就在该块内进行搜索，示例代码如下：

	   /*在对应的block中查找*/
	   for(int i = indexItem.start; i < indexItem.start + indexItem.length; i++) {
	       if(valueList[i] == key)
	           return i;
	    }
	   	return -1;
	}

  如果需要在数组中插入元素，同样需要需要先查找是否存在对应的块，如果存在，则追加到该块中元素的尾部。
  完整示例代码如下：

public class BlockSearch {
	/*主表*/
    static int[] valueList = new int[]{
    	104, 101, 103, 105,102, 0, 0, 0, 0, 0,
        201, 202, 204, 203,0,   0, 0, 0, 0, 0,
        303, 301, 302,  0,   0,   0, 0, 0, 0, 0
    };

    /*索引表*/
    static Block[] indexList = new Block[]{
    	new Block(1, 0, 5),
    	new Block(2, 10, 4),
    	new Block(3, 20, 3)
    };
	
	public static void main(String[] args) {
		System.out.println("原始主表：");
		printElemts(valueList);
		
		/*分块查找*/
		int searchValue = 203;
		System.out.println("元素"+searchValue+"，在列表中的索引为："+blockSearch(searchValue)+"\n");
		
	    /*插入数据并查找*/
		int insertValue = 106;
		         
		/*插入成功，查找插入位置*/
	    if (insertBlock(insertValue)) {
		   System.out.println("插入元素"+insertValue+"后的主表：");
		   printElemts(valueList);
		   System.out.println("元素" + insertValue + "在列表中的索引为：" + blockSearch(insertValue));
	    }
	}
	
	public static void printElemts(int[] array) {
	    for(int i = 0; i < array.length; i++){
	        System.out.print(array[i]+" ");
	        if ((i+1)%10 == 0) {
	            System.out.println();
	        }
	    }
	}
	 
	 
	/*插入数据*/
	public static boolean insertBlock(int key) {
	    Block item = null;

	    /*确定插入到哪个块中，在该例子中，第一个block中放的是100-200之间的数，第二个block中放的是200-300之间的数，以此类推*/
	    int index = key/100;
	    int i = 0;
	    /*找到对应的block*/
	    for (i = 0; i < indexList.length; i++) {
	        if (indexList[i].index == index) {
	            item = indexList[i];
	            break;
	        }
	    }
	    /*如果数组中不存在对应的块，则不能插入该数据*/
	    if (item == null) {
	       return false;
	    }

	    /*将元素插入到每个块的最后*/
	    valueList[item.start + item.length] = key;
	    /*更新该块的长度*/
	    indexList[i].length++;
	    return true;
	} 
	 
	public static int blockSearch(int key) {
	    Block indexItem = null;

	    /*确定插入到哪个块中，在该例子中，第一个block中放的是100-200之间的数，第二个block中放的是200-300之间的数，以此类推*/
	    int index = key/100;
	    /*找到对应的block*/
	    for(int i = 0;i < indexList.length; i++) {
	       if(indexList[i].index == index) {
	           indexItem = indexList[i];
	           break;
	       }
	   }

	    /*如果数组中不存在对应的块，则返回-1，查找失败*/
	   if(indexItem == null)
	       return -1;

	   /*在对应的block中查找*/
	   for(int i = indexItem.start; i < indexItem.start + indexItem.length; i++) {
	       if(valueList[i] == key)
	           return i;
	    }
	   	return -1;
	}
}

  测试结果如下：

原始主表：
104 101 103 105 102 0 0 0 0 0
201 202 204 203 0 0 0 0 0 0
303 301 302 0 0 0 0 0 0 0
元素203，在列表中的索引为：13
插入元素106后的主表：
104 101 103 105 102 106 0 0 0 0
201 202 204 203 0 0 0 0 0 0
303 301 302 0 0 0 0 0 0 0
元素106在列表中的索引为：5

七、哈希查找

7.1 哈希查找介绍

  要了解哈希查找，就要先了解一下哈希表和哈希函数。先看下标准的定义：哈希表，是根据关键值而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表（哈希表）。
  从上面的定义可以看出：哈希查找与线性表查找和树表查找最大的区别在于，不用数值比较。

7.1.1 构造哈希表

  要使用哈希查找，就要先有哈希表，所以需要先介绍一下哈希表的构造方法。常见的构造方法有如下几种：

• 1、直接定址法
    哈希地址：f(key) = a*key+b (a、b为常数)。
    这种方法的优点是：简单、均匀、不会产生冲突。但是需要事先知道 key 的分布情况，适合查找表较小并且连续的情况。
• 2、数字分析法
    假设关键字是R进制数（如十进制）。并且哈希表中可能出现的关键字都是事先知道的，则可选取关键字的若干数位组成哈希地址。选取的原则是使得到的哈希地址尽量避免冲突，即所选数位上的数字尽可能是随机的。
    举个例子：比如11位手机号码“136xxxx5889”，其中前三位是接入号，一般对应不同运营公司的子品牌，中间四位表示归属地，最后四位才是用户号，此时就可以用后4位来作为哈希地址。
• 3、平方取中法
    取key平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况，仅取其中的几位为地址不一定合适。而一个数平方后的中间几位数和数的每一位都相关， 由此得到的哈希地址随机性更大。如key是1234，那么它的平方就是1522756，再抽取中间的3位就是227作为 f(key) 。
• 4、折叠法
    折叠法是将 key 从左到右分割成位数相等的几个部分(最后一部分位数不够可以短些)，然后将这几部分叠加求和，并按哈希表的表长，取后几位作为 f(key) 。
    比如key是9876543210，哈希表的表长为3位，我们将 key 分为4组，987 | 654 | 321 | 0 ，然后将它们叠加求和 987+654+321+0=1962，再取后3位即得到哈希位置是：962 。
• 5、除留余数法
    取关键字被某个不大于哈希表表长 m 的数 p 除后所得的余数为哈希地址。即 f(key) = key % p (p ≤ m)。这种方法是最常用的哈希函数构造方法。
• 6、随机数法
    哈希地址：random(key) ，这里random是随机函数，当 key 的长度不等时，采用这种方法比较合适。

7.1.2 解决冲突

  在使用以上方法计算key对应的哈希地址时，难免会遇到两个key不相等，到计算出来的哈希地址相同的情况，该情况就被称为“冲突”。在构造哈希表，常用如下方式解决冲突：

• 1、开放定址法
    该方法指的是两个key在计算出相同的哈希地址时，后者继续在哈希表中向后寻找空位置，存放改key的方法。举个例子：假如原始的key中有8、15两个元素，哈希表中的长度为7，当使用key % length求余时，两个key会计算出相同的哈希位置。假设哈希表中的1位置已经存放了8，那么15就要从1位置往后寻找空位，假如2位置是空的，就可以把15存放到2位置；假如2位置不空，就要往3位置寻找，以此类推。
• 2、拉链法
    该方法中处理相同位置的方式是：创建一个List，存储相同位置上不同值的key，此处借用网上的一张图来表示：
          

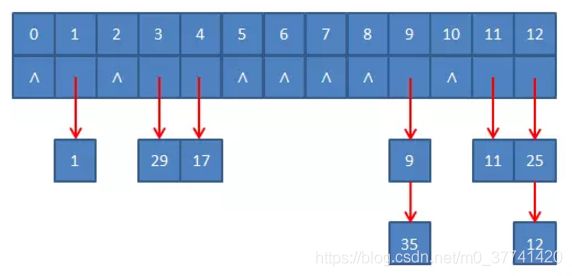
7.2 哈希查找实现

  依据上文介绍，先构建哈希表。而要构建哈希表，就要先有计算地址的方法，示例代码如下：

    /*用除留余数法计算要插入元素的地址*/
    public static int hash(int[] hashTable, int data) {
        return data % hashTable.length;
    }

  有了计算哈希地址的方法后，剩下的就是将原始的元素插入到哈希表中，也就是先利用key计算一个地址，如果这个地址以及有元素了，就继续向后寻找。此处可以循环计算地址，示例代码如下：

    /*将元素插入到哈希表中*/
    public static void insertHashTable(int[] hashTable, int target) {
        int hashAddress = hash(hashTable, target);

        /*如果不为0，则说明发生冲突*/
        while (hashTable[hashAddress] != 0) {
            /*利用开放定址法解决冲突，即向后寻找新地址*/
            hashAddress = (++hashAddress) % hashTable.length;
        }

        /*将元素插入到哈希表中*/
        hashTable[hashAddress] = target;
    }

  哈希表构建后，就是在哈希表中查找元素了。在查找元素时，容易想到的情况是：在直接计算出的哈希地址及其后续位置查找元素。特殊的是，上一步中，有循环计算地址的操作，所以此处计算到原始地址时，也代表查找失败。示例代码如下：

    public static int searchHashTable(int[] hashTable, int target) {
        int hashAddress = hash(hashTable, target);

        while (hashTable[hashAddress] != target) {
            /*寻找原始地址后面的位置*/
            hashAddress = (++hashAddress) % hashTable.length;
            /*查找到开放单元(未存放元素的位置)或 循环回到原点，表示查找失败*/
            if (hashTable[hashAddress] == 0 || hashAddress == hash(hashTable, target)) {
                return -1;
            }
        }
        return hashAddress;
    }

  完整示例代码如下：

public class HashSearch {

    /*待查找序列*/
    static int[] array = {13, 29, 27, 28, 26, 30, 38};
    /* 初始化哈希表长度，此处哈希表容量设置的和array长度一样。
     * 其实正常情况下，哈希表长度应该要长于array长度，因为使用
     * 开放地址法时，可能会多使用一些空位置
     */
    static int hashLength = 7;
    static int[] hashTable = new int[hashLength];

    public static void main(String[] args) {
        /*将元素插入到哈希表中*/
        for (int i = 0; i < array.length; i++) {
        	insertHashTable(hashTable, array[i]);
        }
        System.out.println("哈希表中的数据：");
        printHashTable(hashTable);
        
        int data = 28;
        System.out.println("\n要查找的数据"+data);
        int result = searchHashTable(hashTable, data);
        if (result == -1) {
            System.out.println("对不起，没有找到！");
        } else {
            System.out.println("在哈希表中的位置是：" + result);
        }
    }

    /*将元素插入到哈希表中*/
    public static void insertHashTable(int[] hashTable, int target) {
        int hashAddress = hash(hashTable, target);

        /*如果不为0，则说明发生冲突*/
        while (hashTable[hashAddress] != 0) {
            /*利用开放定址法解决冲突，即向后寻找新地址*/
            hashAddress = (++hashAddress) % hashTable.length;
        }

        /*将元素插入到哈希表中*/
        hashTable[hashAddress] = target;
    }

    public static int searchHashTable(int[] hashTable, int target) {
        int hashAddress = hash(hashTable, target);

        while (hashTable[hashAddress] != target) {
            /*寻找原始地址后面的位置*/
            hashAddress = (++hashAddress) % hashTable.length;
            /*查找到开放单元(未存放元素的位置)或 循环回到原点，表示查找失败*/
            if (hashTable[hashAddress] == 0 || hashAddress == hash(hashTable, target)) {
                return -1;
            }
        }
        return hashAddress;
    }

    /*用除留余数法计算要插入元素的地址*/
    public static int hash(int[] hashTable, int data) {
        return data % hashTable.length;
    }

    public static void printHashTable(int[] hashTable) {
    	for(int i=0;i<hashTable.length;i++)
    		System.out.print(hashTable[i]+" ");
    }
}

  测试结果：

哈希表中的数据：
27 29 28 30 38 26 13
要查找的数据28
在哈希表中的位置是：2