第六章代码题(四)
8.在以孩子兄弟二叉链表存储的树中,求树的叶子结点数。
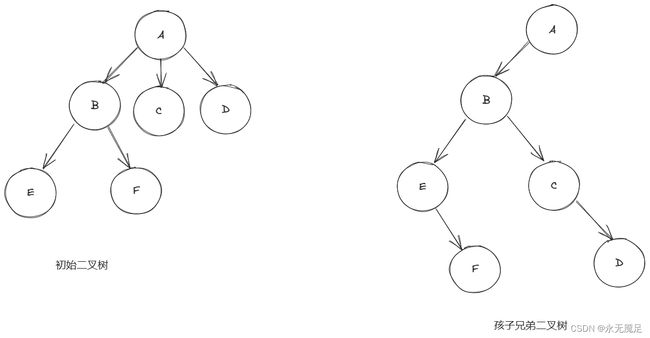
首先要了解孩子兄弟存储结构,简单来说就是每个结点的左孩子不变,在同一层的结点都依次连在该层的结点的右孩子上。 如图 :
将上述的左孩子域改为第一个孩子指针,右孩子域改为右兄弟指针。对结构体进行定义:
//孩子兄弟存储结构
typedef struct CSNode {
ElemType data;
struct CSNode* FirstChild;
struct CSNode* NextSibling;
}CSNode,*CSTree;判断叶子结点的条件应该是当前结点的FirstChild为空。
原因很简单:比如现在有一个结点,它的FirstChild是该结点的孩子,而该结点的NextSibling是它的兄弟;该结点的FirstChild的NextSibling才是该结点的其余孩子,
如果该结点的FirstChild都为空了那其余的都是空谈,结点都为空了肯定不会有兄弟结点,对应的双亲结点也就不会有孩子节点。
其实会做本章的第一道题即求度为2的结点数,这道题也应该会做。只是中间改了一下判定条件。
答案:
int countleafnodes(CSTree cstree) {
if (cstree==NULL)
{
return 0;
}
int k = 0;
//判断为叶子结点时k+1
if (cstree->FirstChild==NULL)
{
k++;
}
k += countleafnodes(cstree->NextSibling);
k += countleafnodes(cstree->FirstChild);
return k;
}验证:
写一个创建结点的方法,在main函数里面直接随便构造一个孩子兄弟二叉树。
// 创建新的节点
struct CSNode* createNode(int data) {
struct CSNode* newNode = (struct CSNode*)malloc(sizeof(struct CSNode));
newNode->data = data;
newNode->FirstChild = NULL;
newNode->NextSibling = NULL;
return newNode;
}main函数:
int main() {
// 创建一个孩子兄弟二叉链表的树示例
struct CSNode* root = createNode(1);
root->FirstChild = createNode(2);
root->FirstChild->NextSibling = createNode(3);
root->FirstChild->NextSibling->FirstChild = createNode(4);
root->FirstChild->NextSibling->FirstChild->NextSibling = createNode(5);
int num = countleafnodes(root);
printf("该孩子兄弟二叉树的叶子结点数为%d", num);
}执行结果:
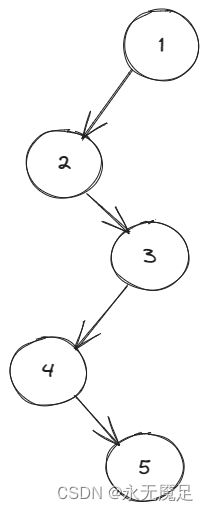
二叉树为:
很明显,值为2,4,5的结点都为叶子结点。所以叶子结点数为3。
9.孩子兄弟二叉链表存储的树中,求树的高度。
注意孩子兄弟二叉链表存储的树的形状可能已经不是一个标准的二叉树了,那么高度就不能像普通二叉树那样求了。
先看求二叉链表存储的二叉树的高度代码:
树的高度其实就是找离根节点路径最长的结点。既然涉及到了最长那么肯定就要有比较了。直接利用math库里面的fmax函数比较。
// 求二叉树的高度
int treehigh(BITree btree) {
if (btree==NULL)
{
return 0;
}
return fmax(treehigh(btree->Lchild), treehigh(btree->Rchild)) + 1;
}接下来看求孩子兄弟二叉链表的二叉树的高度代码:
第一种方法:
孩子兄弟二叉链表的二叉树主要是看结点的FirstChild;而结点的NextSibling和结点在同一层,不影响二叉树的高度。 将孩子兄弟的二叉树仍然按类似普通二叉树的思路进行书写。只是遇到NextSibling返回0,遇到FirstChild返回当前高度加1。
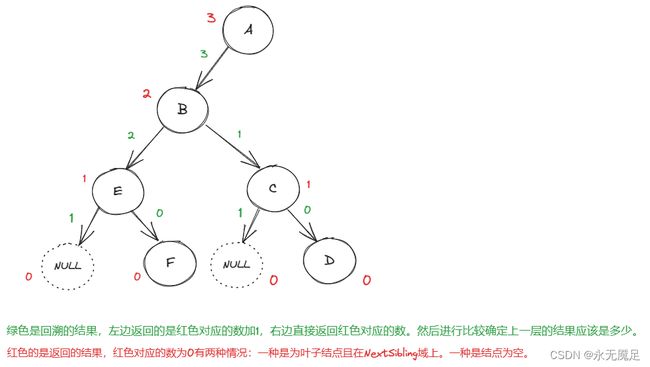
结点为空的时候返回0,为叶子结点时返回参数flag。这种方法主要利用的是递归的回溯,所以可以直接从二叉树的最底层进行解析。随便画一个二叉树:
int dfs(CSTree root, int flag) {
//结点为空时,返回0
if (root==NULL)
{
return 0;
}
//判断是否为叶子结点
if (root->FirstChild == NULL && root->NextSibling==NULL) {
return flag;
}
//拿到左右域判断的
return fmax(dfs(root->FirstChild, 1) + 1, dfs(root->NextSibling, 0));
}
验证:
仍然利用第8题的二叉树进行验证。调用上面的函数即可。
执行结果:
二叉树为:
由图可见二叉树高度为3。
第二种方法:
如果树的根节点为空,那么就返回0,maxHeight记录数的最大高度,while循环遍历根结点的所有子结点,循环中对每个子结点递归调用treeHeight函数,进行比较后返回最大高度+1,加1是因为要算上根节点。
// 计算孩子兄弟树的高度
int treeHeight( CSNode* root) {
if (root == NULL) {
return 0;
}
int maxHeight = 0;
struct CSNode* child = root->FirstChild;
while (child != NULL) {
int height = treeHeight(child);
if (height > maxHeight) {
maxHeight = height;
}
child = child->NextSibling;
}
return maxHeight + 1;
}本方法和第一种方法验证一样,这里不再进行验证。
其实对比标准二叉树和孩子兄弟二叉树可以看到,不论是求叶子结点的个数还是求高度大体思路都是一样的,毕竟不论用哪种存储结构数据结构仍然是二叉树。只是在一些细节方面有略微的区别。
10.实现对顺序存储在一维数组的完全二叉树的先序遍历
按照二叉树节点连续编号的次序,将各结点数据存放到一组连续的存储单元即数组中。为了方便,不使用数组的0号单元,所以数组对应的第i号元素就存储的是二叉树第i个结点。
根据二叉树的性质就有,下标为i的结点的左孩子下标为2i,右孩子下标为2i+1。
(如果要从0开始存储,那么数组中下标为i的元素对应的就是二叉树第i+1个结点。相应地,下标为j的结点左孩子下标为2j+1,右孩子下标为2j+2。)
结构体:
//顺序存储结构
typedef struct {
//0号单元不用
ElemType SqbiTree[MaxSize+1];
int nodemax;
}Bitree;代码:
有索引就好说了,根据上面的性质,以及先序遍历的特点,先输出当前结点的值,然后进行递归,左子树为2*i,右子树为2*i+1。这里要注意,静态数组有容量上限,所以进行递归前要进行判定,没有超出容量上限才能进行递归。
void BeforeTraversal_Sq(Bitree* btree,int i) {
printf("%d", btree->SqbiTree[i]);
if (2*i这上面有个细节:为什么两个判定条件是<而不是<=呢?
当MaxSize为奇数时,数组的最后一个下标就是MaxSize为奇数(因为最大容量为MaxSize+1),那么2*i就不能取<=,因为2*i是偶数,如果取<=,在2*i=MaxSize+1时刚好可以进行递归,这样就会发生数组越界。
同理,当MaxSize为偶数时,2*i+1就不能取<=。
所以综合以上情况,两个判定条件都取<即可。
如果非要取<=,那么在输出前也加个判定条件也可以避免上述情况,代码如下:
void BeforeTraversal_Sq(Bitree* btree,int i) {
if (iSqbiTree[i]);
}
if (2*i<=MaxSize+1)
{
BeforeTraversal_Sq(btree, 2 * i);
}
if (2*i+1<=MaxSize+1)
{
BeforeTraversal_Sq(btree, 2 * i+1);
}
} 还要注意一点,在C语言中,数组下标越界不会引发编译器错误或运行时错误。当你输出一个超出数组范围的下标时,C语言会尝试将该下标转换为对应的内存地址,并将该地址的内容作为输出。这可能是数组之后的内存空间,或者可能是其他全局或局部变量的地址。
验证:
写一个创建顺序存储结构的二叉树的函数:
void createSqBitree(Bitree* btree) {
int a;
for (int i = 1; i SqbiTree[i] = a;
}
} main函数如下:
int main() {
//第十题
Bitree* btree = (Bitree*) malloc (sizeof(Bitree));
createSqBitree(btree);
BeforeTraversal_Sq(btree, 1);
}执行结果:
二叉树如下: