leetcode之合并区间
题目描述:
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 104
通过次数405,696提交次数840,652
解题思路
第一步:排序,按照每个区间的第一个值进行排序,保证后面的区间的左值只有两种情况:1.要么大于前面区间的右值,2.或者小于等于前面区间的右值
第二步:遍历排序后的列表,合并有交集的区间,添加独立的区间到结果集中
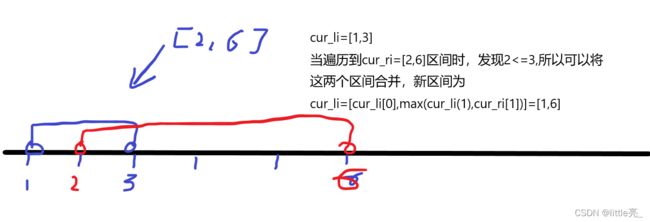
以intervals = [[1,3],[2,6],[8,10],[15,18]]为例,
首先排序得到:intervals = [[1,3],[2,6],[8,10],[15,18]]
当前区间cur_li=[1,3]
下一个区间[2,6]
当发现下一个区间和当前区间不能合并时,直接将当前区间添加到结果集。
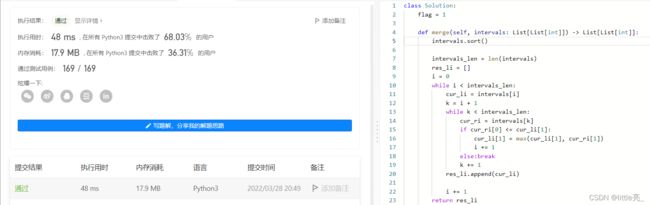
源码
from typing import List
class Solution:
flag = 1
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort() # 按第一个数字排序
intervals_len = len(intervals)
res_li = []
i = 0
while i < intervals_len:
cur_li = intervals[i] #当前区间
k = i + 1
while k < intervals_len:
cur_ri = intervals[k] # 当前的区间
if cur_ri[0] <= cur_li[1]: # 如果右边区间的左值小于等于左边区间的右值,那么这两个区间可以合并
cur_li[1] = max(cur_li[1], cur_ri[1]) # 合并区间
i += 1 # 区间被合并,i的值应该加一,向前移动一次
else:break
k += 1
res_li.append(cur_li) # 加入当前区间(不管该区间有没有合并)
i += 1
return res_li通过截图:
同步更新于个人博客系统:leetcode之合并区间