三维空间中如何寻找和一组给定直线垂直程度最高的直线

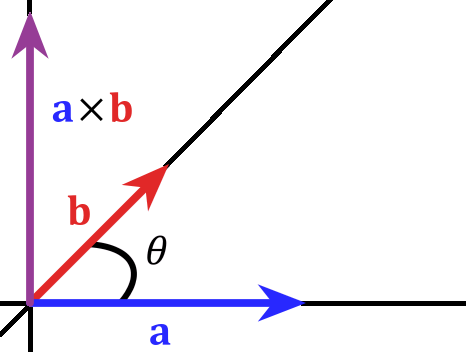
这是个挺有意思的小问题，给定一组直线(至少两条不平行)，希望能找到和这组直线尽可能垂直的直线。打个比方，比如在三维空间中，如下图(forked from wiki)

a和b分别是在一个平面上不平行的两条直线上，那么显而易见与a和b所在直线垂直程度最高的就是与a和b俩俩垂直的竖线，也就是叉积axb方向平行的直线。两条直线可以用叉积，那么多于两条的情况呢？想象如果又有了一条直线，其一端的方向可以用向量c表示，如果c和a、b在一个平面上的话，那么好办，还是axb，或者bxc也行；但是如果c和a、b不在一个平面上的话，那么叉积的办法就不管用了。回到问题的最开始，其实是如何定义和其他直线最大程度垂直。还是考虑只有a和b的情况，axb其实就是在a和b上的投影均为零，也就是点积为零，所以不妨把在其他所有向量上投影最少的向量定义为最大程度垂直的方向。

那么考虑有n条直线，对应n个单位向量代表每条直线的一个方向，其中第i个向量可以表示为\({{v}_{i}}=\left( {{x}_{i}},{{y}_{i}},{{z}_{i}} \right)\)，那么对于一个向量\(v=\left( x,y,z \right)\)，在\({{v}_{i}}\)上投影的长度为：

\[\begin{align}
 & \left| \left\langle v,{{v}_{i}} \right\rangle  \right|=\left| x{{x}_{i}}+y{{y}_{i}}+z{{z}_{i}} \right| \\
\end{align}\]

那么一个很直接的办法就是用优化算法来求出使投影绝对值之和最小的v：

\(\text{min: }\sum\limits_{i=1}^{n}{\left| \left\langle v,{{v}_{i}} \right\rangle  \right|}\)
\(\begin{align}
 & \text{subject to: }\left| {{v}_{i}} \right|=1\text{ and }\left| v \right|=1 \\
\end{align}\)

\(\left| {{v}_{i}} \right|=1\)是为了是每一个向量上的投影能够相加比较，\(\left| v \right|=1\)是为了优化，否则最后的结果就是\(\left( 0,0,0 \right)\)。这个方法固然直观，但是考虑到1)要利用绝对值相加，2)要利用优化算法还是觉得有些麻烦。考虑一下用平方和作为优化目标，当然这会和绝对值的办法有些许不一样，主要是每一个投影大小对结果影响的sensitivity变了，不过总体而言是差不多的，总之，要求的目标变成了：

\( \sum\limits_{i=1}^{n}{{{\left\langle v,{{v}_{i}} \right\rangle }^{2}}} \)
\( =\sum\limits_{i=1}^{n}{{{\left( x{{x}_{i}}+y{{y}_{i}}+z{{z}_{i}} \right)}^{2}}} \)
\( =\sum\limits_{i=1}^{n}{{{x}^{2}}{{x}_{i}}^{2}+{{y}^{2}}{{y}_{i}}^{2}+{{z}^{2}}{{z}_{i}}^{2}+2xy{{x}_{i}}{{y}_{i}}+2yz{{y}_{i}}{{z}_{i}}+2zx{{z}_{i}}{{x}_{i}}} \)
\( ={{x}^{2}}\sum\limits_{i=1}^{n}{{{x}_{i}}^{2}}+{{y}^{2}}\sum\limits_{i=1}^{n}{{{y}_{i}}^{2}}+{{z}^{2}}\sum\limits_{i=1}^{n}{{{z}_{i}}^{2}}+xy\sum\limits_{i=1}^{n}{2{{x}_{i}}{{y}_{i}}}+yz\sum\limits_{i=1}^{n}{2{{y}_{i}}{{z}_{i}}}+zx\sum\limits_{i=1}^{n}{2{{z}_{i}}{{x}_{i}}} \)
\(\begin{align}
&\\
\end{align}\)

注意观察最后的展开，如果右边加个等于常数项的话，就是个椭球嘛，而且没有一次项，所以是个中心在原点的椭球。这样一来就很简单了，考虑之前提出的限制条件\(\left| v \right|=1\)，相当于有一个半径为1，球心在原点的球面，和一个中心也在原点，大小未定，但是三个极轴比例确定的椭球面。我们要寻找这么一种情况：球面和椭球面有交点(v存在)，并且椭球的轴长尽可能小(\(\sum\limits_{i=1}^{n}{{{\left\langle v,{{v}_{i}} \right\rangle }^{2}}}\)最小)。很显然这种情况就是椭球内切于单位球面，而此时v对应的就是长轴的方向，所以问题就更简单了，我们都不需要求出椭球的具体表达式，而是找出长轴的方向向量就可以了。回顾一下椭球的知识：任意一个椭球可以表达如下：

\(\begin{align}
 & {{\left( v-{{v}_{0}} \right)}^{T}}M\left( v-{{v}_{0}} \right)=1 \\
\end{align}\)

其中v0是中心坐标，当然对于本文的情况这是个零向量，M的特征向量就是三个极轴的方向，特征值就是三个轴半长的平方分之一，所以我们只要求出M，然后找到M对应特征值绝对值最小的那个特征向量，该向量就是我们最终要求的方向向量v。所以，将椭球表达式展开，为简便，首先假设M如下：

\(\begin{align}
&M=\left[ \begin{matrix}
   A & D & F  \\
   D & B & E  \\
   F & E & C  \\
\end{matrix} \right]\\
\end{align}\)

于是有：

\( {{v}^{T}}Mv \)
\( ={{\left[ \begin{matrix}
   x  \\
   y  \\
   z  \\
\end{matrix} \right]}^{T}}\left[ \begin{matrix}
   A & D & F  \\
   D & B & E  \\
   F & E & C  \\
\end{matrix} \right]\left[ \begin{matrix}
   x  \\
   y  \\
   z  \\
\end{matrix} \right] \)
\( =A{{x}^{2}}+B{{y}^{2}}+C{{z}^{2}}+2Dxy+2Eyz+2Fzx \)
\[\begin{align}
&\\
\end{align}\]

把这个结果和前面的公式(3)对照，得到A、B、C、D、E和F的值，代入M，得到如下：

\(\begin{align}
&M=\left[ \begin{matrix}
   \sum\limits_{i=1}^{n}{{{x}_{i}}^{2}} & \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} & \sum\limits_{i=1}^{n}{{{z}_{i}}{{x}_{i}}}  \\
   \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} & \sum\limits_{i=1}^{n}{{{y}_{i}}^{2}} & \sum\limits_{i=1}^{n}{{{y}_{i}}{{z}_{i}}}  \\
   \sum\limits_{i=1}^{n}{{{z}_{i}}{{x}_{i}}} & \sum\limits_{i=1}^{n}{{{y}_{i}}{{z}_{i}}} & \sum\limits_{i=1}^{n}{{{z}_{i}}^{2}}  \\
\end{matrix} \right]\\
\end{align}\)

对这个矩阵求绝对特征值最小的特征向量，就得到了最大程度垂直于给定直线的向量了。需要注意的是当所有给定直线在一个平面时，M不满秩，不过这种情况恰好对应绝对值最小的特征值就是0，所以应用到这个算法里还是没有问题。这个办法还可以类似地推广到二维或者更高维，只不过对三维以上的情况矩阵不满秩的处理会比较麻烦一些。

下面是三维情况下的一段Python验证程序：

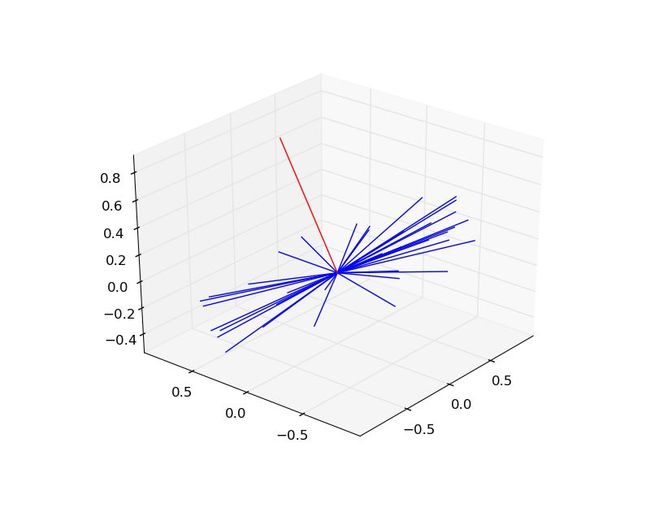
 1 from __future__ import division
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 from mpl_toolkits.mplot3d import Axes3D
 5 
 6 # Distance from x to the plane with v as the normal vector, passing through (0, 0, 0)
 7 d = lambda x, v: abs(x[0]*v[0]+x[1]*v[1]+x[2]*v[2]) / np.linalg.norm(v)
 8 
 9 # Random normal vector for test
10 norm_v_plane = np.random.randn(3)
11 N = 200
12 
13 # Generate test unit vectors that within 0.2 to the test plane
14 v_test = [x for x in [x/np.linalg.norm(x) for x in np.random.randn(N, 3)] if d(x, norm_v_plane) < 0.2]
15 
16 # Plot test vectors
17 fig = plt.figure('Minimum dot product vector')
18 ax = fig.add_subplot(111, projection='3d')
19 for v in v_test:
20     ax.plot([0, v[0]], [0, v[1]], [0, v[2]], 'b')
21 
22 # Calculate the coefficients matrix of the arbitrary ellipsoid
23 A, B, C, D, E, F = [0] * 6
24 for v in v_test:
25     x, y, z = v
26     A += x * x
27     B += y * y
28     C += z * z
29     D += x * y
30     E += y * z  
31     F += x * z
32 M = np.array([[A, D, F],
33               [D, B, E], 
34               [F, E, C]])
35 
36 # Pick the eigenvector with the minimum egienvalue
37 u, v = np.linalg.eig(M)
38 vp = v[:, np.argmin(np.abs(u))]
39 if vp[2] < 0:
40     vp = -vp
41 
42 ax.plot([0, vp[0]], [0, vp[1]], [0, vp[2]], 'r')
43 
44 plt.show()

 

这段小程序会随机选取一个过原点的平面，然后在距离平面0.2的距离范围内产生一些随机向量，然后找到最大程度垂直于这些向量的向量，比如下图：