LeetCode：121.买卖股票的最佳时机——动态规划

道阻且长，行则将至。

---

算法，不如说它是一种思考方式

算法专栏： 123
关于动态规划：LeetCode：322. 零钱兑换——动态规划从案例入门

---

一、121. 买卖股票的最佳时机

• 题目描述：给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
  你只能选择某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
  返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

• 来源：力扣（LeetCode）

• 难度：简单

• 提示：
  1 <= prices.length <= 105
  0 <= prices[i] <= 104

• 示例 1：
  输入：[7,1,5,3,6,4]
  输出：5
  解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
  示例 2：
  输入：prices = [7,6,4,3,1]
  输出：0
  解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

解题

1.暴力求解

其实就是求取一个最好的收益交易日组合，很容易可以写出用两层for循环暴力求解的方法，最后暴力最大收益。

• code：

class Solution {
    public int maxProfit(int[] prices) {
        int ans=0;
        for(int i=0;i<prices.length;i++){
            for(int j=i+1;j<prices.length;j++){
                if(prices[j]>prices[i]){
                    int t=prices[j]-prices[i];
                    ans=ans>t?ans:t;
                }
            }
        }
        return ans;
    }
}

时间复杂度是O(n²)，最后当然是超时了。

2.动态规划

本题可以使用动态规划来解决，动态规划的实质：以空间换时间。就是说动态规划通过维护一个dp数组来减少时间复杂度。

• 那这个dp数组应该如何建立。我们看到题，交易有买和卖，两个不同的操作，我们理所当然的建立两个数组。我们就建立一个二维数组：int[][]dp=new int[prices.length][2]; dp[i][0]就代表第i天内买进的最佳收益（或者说最佳买进机会、代价），dp[i][1]代表第i天内卖出的最佳收益。

• 那这个状态转移方程怎么确定。对于dp[i][0]，我们要根据前一个状态推出后一个状态，前一个状态表示在前i-1天买进股票最佳是m，而第i天股票价格是n的话，我们就确定n和m谁价格更低就是第i天的状态，因此dp[i][0]=Math.max{ dp[i-1][0] , -price[i] }（由于买进其是花钱，我们使用负的代表的支出意思，也可以理解为一开始收益0-m）。dp[i][1]是在这一天卖出，价格就可以计算为prices[i] - dp[i-1][0]，就是说今天的价格减去之前最佳买的，然后和前一天的最佳收益比较确定当前状态，因此dp[i][1]=Math.max{ dp[i-1][1] , price[i]-dp[i-1][0] }。

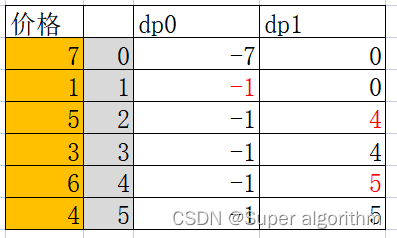
• 确定初始状态，最初的状态dp[0][:]（第一天买入和卖出收益）根据问题示例1来看，第一天买入就是花费7元，dp[0][0]=-7，第一天无收益dp[0][1]=0。然后根据状态转移方程就可以确定之后的每一天的状态了。
  示例1就可以推出：最大利润是5
  

• code：

class Solution {
    public int maxProfit(int[] prices) {

        int[][]dp=new int[prices.length][2];
        dp[0][0]-=prices[0];
        dp[0][1]=0;
        for(int i=1;i<prices.length;i++){
            dp[i][0]=Math.max(dp[i-1][0],-prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]);
        }
        return dp[prices.length-1][1];
    }
}

3.贪心策略

从前面的思路我们会发现，这个过程不就是在找一个今天之前的最便宜买进日，于是我们可以不使用dp数组了：使用一个min来记录。

• code:

class Solution {
    public int maxProfit(int[] prices) {
        int ans=0;
        int min=99999999;
        int t;
        for(int i=1;i<prices.length;i++){
            min=min<prices[i-1]?min:prices[i-1];
            //min=Math.min(min,prices[i-1]);
            if(prices[i]>min) {
                t = prices[i] - min;
                ans = ans > t ? ans : t;
                //ans=Math.max(ans,t);
            }
        }
        return ans;
    }
}

有没有发现这个方法节约了数组开销，但是内存消耗反而增加了。

---

二、122. 买卖股票的最佳时机II

• 题目描述：给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
  在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
  返回 你能获得的 最大 利润 。

• 来源：力扣（LeetCode）

• 难度：中等

• 提示：
  1 <= prices.length <= 3 * 104
  0 <= prices[i] <= 104

• 示例 1：
  输入：prices = [7,1,5,3,6,4]
  输出：7
  解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
  随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
  总利润为 4 + 3 = 7 。
  示例 2：
  输入：prices = [1,2,3,4,5]
  输出：4
  解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
  总利润为 4 。
  示例 3：
  输入：prices = [7,6,4,3,1]
  输出：0
  解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

解题

这一和上一题不一样在于不限制交易次数了，题中说“你也可以先购买，然后在同一天出售。”，这个就是0收益不需要管。

1.贪心法

贪心法就是让我们把每一个可以隔1天（一天之内交易是无收益的）获取收益的加起来，这个结果就是我们可以获得的最大收益。例如示例1就是一个最鲜明的例子，可能说这个太特殊了，刚好是隔1天的情况。那把prices = [7,1,5,3,6,4]改为prices2 = [7,1,5,3,4,6]，虽然发生改动，但是他们的结果是不会变。那么我们来看prices2 ，1,5是一个肯定的收益，3,4,6可能觉得应该是6-3的收益，而6-3=（6-4）+（4-3），所以贪心法的方法来计算是可以获取最优解的。

• code：

class Solution {
    public int maxProfit(int[] prices) {
        int ans=0;
        for (int i = 0; i < prices.length-1; i++) {
            if(prices[i]<prices[i+1]){
                ans=ans+ prices[i+1] - prices[i];
            }
        }
        return ans;
    }
}

2.动态规划

与上一题类似。

• dp数组。建立一个二维数组：int[][]dp=new int[prices.length][2]; dp[i][0]就代表第i天内买进的最佳收益（或者说最佳买进机会、代价），dp[i][1]代表第i天内卖出的最佳收益。

• 那这个状态转移方程怎么确定。对于dp[i][0]，本题相比较上一题，有多次收益的可能性，因此更新就需要考虑之前的收益情况，所以要使用之前收益-price[i]代表该买进最佳收益，dp[i][0]=Math.max{ dp[i-1][0] , dp[i-1][1]-price[i] }。dp[i][1]是在这一天卖出，价格就可以计算为prices[i] - dp[i-1][0]，就是说今天的价格减去之前最佳买的，然后和前一天的最佳收益比较确定当前状态，因此dp[i][1]=Math.max{ dp[i-1][1] , price[i]-dp[i-1][0] }。

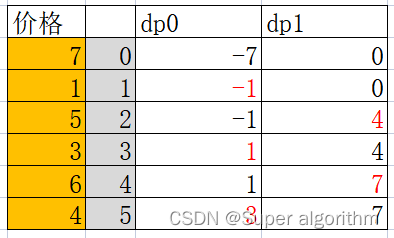
• 确定初始状态，最初的状态dp[0][:]（第一天买入和卖出收益）根据问题示例1来看，第一天买入就是花费7元，dp[0][0]=-7，第一天无收益dp[0][1]=0。然后根据状态转移方程就可以确定之后的每一天的状态了。
  

• code：

class Solution {
    public int maxProfit(int[] prices) {
        int[][]dp=new int[prices.length][2];
        dp[0][0]-=prices[0];
        dp[0][1]=0;
        for(int i=1;i<prices.length;i++){
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]);
        }
        return dp[prices.length-1][1];
    }
}

---

Bug本是code常态，通过才是稀缺的意外！

返回第一页。☝

---

☕物有本末，事有终始，知所先后。

☝☝☝☝☝我的CSDN☝☝☝☝☝☝