matlab使用教程(12)—随机数种子和随机数流
1.生成可重复的随机数
1.1指定种子
本示例显示如何通过首先指定种子来重复生成随机数数组。每次使用相同种子初始化生成器时,始终都可以获得相同的结果。首先,初始化随机数生成器,以使本示例中的结果具备可重复性。
rng( 'default' );
现在使用种子 1 初始化生成器。
rng(1);
然后创建随机数数组。
A = rand(3,3)
A =
0.4170 0.3023 0.1863
0.7203 0.1468 0.3456
0.0001 0.0923 0.3968
重复同样的命令。
A = rand(3,3)
A =
0.5388 0.2045 0.6705
0.4192 0.8781 0.4173
0.6852 0.0274 0.5587
第一次调用 rand 改变了生成器的状态,所以第二次调用的结果不同。现在使用之前的种子重新初始化生成器。然后将再次生成第一个矩阵 A 。
rng(1);
A = rand(3,3)
A =
0.4170 0.3023 0.1863
0.7203 0.1468 0.3456
0.0001 0.0923 0.3968
在某些情况下,只设定种子并不能保证相同的结果。这是因为代码执行时,随机数函数所用的生成器可能与您所期望的不同。要确保长期可重复性,应同时指定种子和生成器类型。
例如,以下代码将种子设定为 1 并将生成器设置为梅森旋转。
rng(1, 'twister' );
当您希望实现下列结果时,应同时设置种子和生成器:
• 应确保如今编写的代码在以后的 MATLAB 版本中运行时该时可返回相同的结果。
• 应确保在使用当前版本时,您在以前 MATLAB 版本中编写的代码可返回相同的结果。
• 在运行他人的随机数代码之后,再重复自己代码的随机数。
1.2保存和恢复生成器设置
本示例显示如何通过保存和恢复生成器设置来创建可重复随机数数组。需要保存和恢复生成器设置的最常见原因是为了重现算法或迭代中某一特定点产生的随机数。例如,可以在调试时使用生成器设置作为辅助工具。与重新提供种子(该方法会对生成器进行重新初始化)不同,此方法让您能够随时保存和恢复生成器的设置。
首先,初始化随机数生成器,以使本示例中的结果具备可重复性。
rng(1, 'twister' );
创建 1 到 10 之间的随机整数值数组。
A = randi(10,3,3)
A = 3×3
5 4 2
8 2 4
1 1 4
第一次调用 randi 改变了生成器的状态。在第一次调用结构体 s 中的 randi 后,保存生成器设置。
s = rng;
创建另一个由 1 到 10 之间的随机整数值组成的数组。
A = randi(10,3,3)
A = 3×3
6 3 7
5 9 5
7 1 6
现在,将生成器恢复为在 s 中存储的以前状态,并重新生成第二个数组 A 。
rng(s);
A = randi(10,3,3)
A = 3×3
6 3 7
5 9 5
7 1 6
2.生成不同的随机数
本示例显示在 MATLAB 重新启动时如何避免重复生成相同的随机数数组。当您要将在不同的 MATLAB 会话中执行的相同随机数命令结果合并在一起时,这种方法非常有用。所有随机数函数( rand 、 randn 、 randi 和 randperm)均可从共享随机数生成器中抽取值。每次启动MATLAB 时,生成器均复位到相同的状态。因此,当启动后立即执行计算的任何时候,类似 rand(2,2) 的命令均返回相同的结果。此外,无论何时重新启动,任何调用随机数函数的脚本或函数均返回相同的结果。
一种获得不同随机数的方法是每次使用不同的种子初始化生成器。这样做可确保不会重复出现上一次会话的结果。
在调用任何随机数函数之前,在 MATLAB 会话执行一次 rng('shuffle') 命令。
rng( 'shuffle' )
可以在 MATLAB 命令行窗口中执行此命令,也可以将其添加到启动文件中,这是 MATLAB 每次重新启动时都要执行的特殊脚本。现在执行随机数命令。
A = rand(2,2);
在每次调用 rng('shuffle') 时,它都根据当前的时间使用不同的种子重新设定生成器的种子。
注意 频繁地重新设定生成器的种子既不会改进输出的统计特性,也不会在真正意义上使输出更加随机。在重启 MATLAB 时或在运行涉及随机数的大型计算之前重新设定种子非常有用。然而,在一个会话中过于频繁地重新设定生成器的种子并不是理想的做法,因为随机数的统计特性会受到不利影响。或者,在不同 MATLAB 会话中显式指定不同种子。例如,在一个 MATLAB 会话中生成随机数。
rng(1);
A = rand(2,2);
在另一个 MATLAB 会话中使用不同种子生成随机数。
rng(2);
B = rand(2,2);
数组 A 和 B 不同,因为在每次调用 rand 函数之前,都会用不同的种子对生成器进行初始化。要生成保证不重叠的多个独立流,并且已对其执行证明流之间值的独立性的测试,可以使用
RandStream.create 。
3.使用 RandStream 管理全局流
rand、 randn 、 randi 和 randperm 从称为全局流的基础随机数流获取随机数。全局流是一个
RandStream 对象。控制全局流的简单方法是使用 rng 函数。为了进行更全面的控制, RandStream 类使您能够从全局流创建一个单独的流,获得全局流的句柄,并控制随机数生成。
使用 rng 将随机数生成器设置为默认的种子 ( 0 ) 和算法(梅森旋转)。保存生成器设置。
rng( 'default' )
s = rng
s = struct with fields:
Type: 'twister'
Seed: 0
State: [625x1 uint32]
创建一个由 0 和 1 之间的均匀分布随机值组成的 1×6 行向量。
x = rand(1,6)
x = 1×6
0.8147 0.9058 0.1270 0.9134 0.6324 0.0975
使用 RandStream.getGlobalStream 返回全局流的句柄,即 rand 从中生成随机数的当前全局流。如果您使用 RandStream.getGlobalStream 获取全局流的句柄,您可以看到您使用 rng 对全局流所做的更改。
globalStream = RandStream.getGlobalStream
globalStream =
mt19937ar random stream (current global stream)
Seed: 0
NormalTransform: Ziggurat
更改生成器种子和算法,并创建一个新的随机行向量。显示 rand 从中生成随机数的当前全局流。
rng(1, 'philox' )
xnew = rand(1,6)
xnew = 1×6
0.5361 0.2319 0.7753 0.2390 0.0036 0.5262
globalStream = RandStream.getGlobalStream
globalStream =
philox4x32_10 random stream (current global stream)
Seed: 1
NormalTransform: Inversion
接下来,还原原始生成器设置并创建一个随机向量。结果与用默认生成器创建的原始行向量 x 相匹配。
rng(s)
xold = rand(1,6)
xold = 1×6
0.8147 0.9058 0.1270 0.9134 0.6324 0.0975
默认情况下,随机数生成函数(如 rand )使用全局随机数流。要指定不同流,请创建另一个
RandStream 对象。将其作为第一个输入参数传递给 rand。例如,使用面向 SIMD 的快速梅森旋转创建一个 1×6 随机数向量。
myStream = RandStream( 'dsfmt19937' )
myStream =
dsfmt19937 random stream
Seed: 0
NormalTransform: Ziggurat
r = rand(myStream,1,6)
r = 1×6
0.0306 0.2131 0.2990 0.3811 0.8635 0.1334
当您以 myStream 作为第一个输入参数调用 rand 函数时,它从 myStream 中获取数字,并且不影响全局流的结果。
如果要将 myStream 设置为全局流,可以使用 RandStream.setGlobalStream 对象函数。
RandStream.setGlobalStream(myStream)
globalStream = RandStream.getGlobalStream
globalStream =
dsfmt19937 random stream (current global stream)
Seed: 0
NormalTransform: Ziggurat
在许多情况下,控制全局流只需使用 rng 函数,但 RandStream 类允许控制一些高类功能,如选择用于正态随机值的算法。
例如,创建一个 RandStream 对象,并指定转换算法,以便在使用 randn 时生成正态分布的伪随机值。使用 Polar 转换算法而不是默认的 Ziggurat 转换算法生成正态分布的伪随机值。
myStream = RandStream( 'mt19937ar' , 'NormalTransform' , 'Polar' )
myStream =
mt19937ar random stream
Seed: 0
NormalTransform: Polar
将 myStream 设置为全局流。从全局流中创建 6 个正态分布的随机数。
RandStream.setGlobalStream(myStream)
randn(1,6)
ans = 1×6
0.2543 -0.7733 -1.7416 0.3686 0.5965 -0.0191
4.创建和控制随机数流
通过 RandStream 类,可以创建随机数流。在很多情况下,这是很有用的:
• 您可以生成随机值,而不影响全局流的状态。
• 您可以在仿真中分离随机性的来源。
• 您使用的生成器可以与 MATLAB 软件在启动时使用的生成器不同。
使用 RandStream 对象,您可以创建自己的流,设置可写属性,并使用该流生成随机数。可以采用控制全局流的相同方式来控制所创建的流,甚至可将全局流替换为所创建的流。要创建流,请使用 RandStream 函数。
myStream = RandStream( 'mlfg6331_64' );
rand(myStream,1,5)
ans =
0.6986 0.7413 0.4239 0.6914 0.7255
随机流 myStream 的行为与全局流的行为不同。如果以 myStream 作为第一个参数调用 rand、randn 、 randi 和 randperm 函数,它们将从您创建的流中获取。如果您调用 rand 、 randn 、 randi 和 randperm 而不使用 myStream,它们将从全局流中获取。可以使用 RandStream.setGlobalStream 方法使 myStream 成为全局流。
RandStream.setGlobalStream(myStream)
RandStream.getGlobalStream
ans =
mlfg6331_64 random stream (current global stream)
Seed: 0
NormalTransform: Ziggurat
RandStream.getGlobalStream == myStream
ans =
1
4.1子流
您可以使用子流来获得在统计上独立于流的不同结果。与种子不同(在种子中,沿随机数序列的位置并不完全已知),子流之间的间隔是已知的,因此可以消除任何重叠的机会。简而言之,子流能够以更可控的方式完成在传统上用种子所做的许多事情。子流也是比并行流更轻量级的解决方案。通过子流,可以快速轻松地确保在不同时间从相同的代码中得到不同结果。要使用 RandStream 对象的Substream 属性,请使用支持子流的生成器创建流。有关支持子流及其属性的生成器算法的列表,请参阅下一节中的表。例如,在循环中生成几个随机数。
myStream = RandStream( 'mlfg6331_64' );
RandStream.setGlobalStream(myStream)
for i = 1:5
myStream.Substream = i;
z = rand(1,i)
end
z =
0.6986
z =
0.9230 0.2489
z =
0.0261 0.2530 0.0737
z =
0.3220 0.7405 0.1983 0.1052
z =
0.2067 0.2417 0.9777 0.5970 0.4187
在另一个循环中,您可以生成独立于第一组(包含 5 次)迭代的随机值。
for i = 6:10
myStream.Substream = i;
z = rand(1,11-i)
end
z =
0.2650 0.8229 0.2479 0.0247 0.4581
z =
0.3963 0.7445 0.7734 0.9113
z =
0.2758 0.3662 0.7979
z =
0.6814 0.5150
z =
0.5247
子流在序列计算中很有用。子流可以通过返回到流中的特定检查点来重新创建所有或部分仿真。例如,您可以返回到循环中的第 6 个子流。结果包含与上述第 6 个输出相同的值。
myStream.Substream = 6;
z = rand(1,5)
z =
0.2650 0.8229 0.2479 0.0247 0.4581
4.2选择随机数生成器
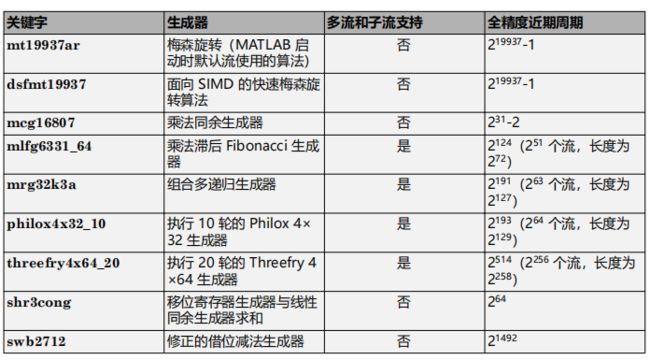
MATLAB 提供了多个生成器算法选项。下表概述了可用的生成器算法的关键属性以及用于创建这些算法的关键字。要返回所有可用生成器算法的列表,请使用 RandStream.list 方法。
生成器 mcg16807 、 shr3cong 和 swb2712 可与以前的 MATLAB 版本向后兼容。mt19937ar 和 dsfmt19937 主要是为序列应用程序设计的。其余的生成器明确支持并行随机数生成。根据应用情况,某些生成器可能会更快或者返回精度更高的值。所有伪随机数生成器均基于确定性算法,并且所有生成器都通过足够具体的随机性统计学测试。检查蒙特卡罗模拟结果的一种方法是使用两种或更多种不同的生成器算法重新运行该仿真,MATLAB 中的生成器选项提供了执行该操作的方式。使用不同的生成器时,尽管结果不可能因多个蒙特卡罗采样误差而异,但资料中存在此类验证在特定的生成器算法中出现缺陷的示例。
4.3生成器算法
1)mt19937ar
梅森旋转算法的周期为 2 19937 − 1,并且每个 U(0,1) 值都是使用两个 32 位整数生成的。可能的值为 (0, 1) 区间内 2 −53 的倍数。此生成器不支持多个流或子流。默认情况下用于mt19937ar 流的 randn 算法为 ziggurat 算法 [7],但基于 mt19937ar 生成器。
注意 此生成器与 rand 函数从 MATLAB 版本 7 开始使用的生成器相同,通过 rand('twister',s) 激
活。
2)dsfmt19937
面向 SIMD 的双精度快速梅森旋转算法(如 [12] 中所述)是速度更快的梅森旋转算法实现。周期为2 19937 − 1 ,可能的值为 (0, 1) 区间内 2 −52 的倍数。生成器本身会生成 [1, 2) 内的双精度值,这些值经过变换生成 U(0,1) 值。此生成器不支持多个流或子流。
3)mcg16807
32 位乘法同余生成器,如 [14] 中所述,其中乘数为 a = 7 5 ,模为 m = 2 31 − 1。此生成器的周期为2 31 − 2,不支持多个流或子流。每个 U(0,1) 值都是使用单个 32 位整数通过该生成器创建的;可能的值为 (2 31 − 1) −1 的所有倍数(严格位于区间 (0, 1) 内)。对于 mcg16807 流, randn 使用的默认算法是极坐标算法。
注意 此生成器与 rand 和 randn 函数从 MATLAB 版本 4 开始使用的生成器相同,通过
rand('seed',s) 或 randn('seed',s) 进行激活。
4)mlfg6331_64
64 位的乘法滞后 Fibonacci 生成器,如 [10] 中所述,其中滞后值为 l = 63 、 k = 31。此生成器与SPRNG 包中实现的 MLFG 类似。其周期约为 2 124 。通过参数化,它最多支持 2 61 个并行流以及 2 51个长度均为 2 72 的子流。每个 U(0,1) 值都是使用一个 64 位整数通过该生成器创建的;可能的值为2 −64 的所有倍数(严格位于区间 (0, 1) 内)。默认情况下用于 mlfg6331_64 流的 randn 算法为ziggurat 算法 [7],但基于 mlfg6331_64 生成器。
5)mrg32k3a
32 位组合多递归生成器,如[2]中所述。此生成器类似于在 C 语言的 RngStreams 包中实现的 CMRG。其周期为 2 191 ,通过序列分割支持多达 2 63 个并行流,每个流的长度为 2 127 。它还支持 2 51个长度均为 2 76 的子流。每个 U(0,1) 值都是使用两个 32 位整数通过该生成器创建的;可能的值为2 −53 的倍数(严格位于区间 (0, 1) 内)。默认情况下用于 mrg32k3a 流的 randn 算法为 ziggurat算法 [7],但基于 mrg32k3a 生成器。
6)philox4x32_10
执行 10 轮的 4×32 生成器,如 [15] 中所述。此生成器使用 Feistel 网络和整数乘法。该生成器专为高并行系统(如 GPU)的高性能而设计。它的周期为 2 193 (2 64 个流,长度为 2 129 )。
threefry4x64_20执行 20 轮的 4×64 生成器,如 [15] 中所述。此生成器是 Skein 散列函数中的 Threefish 块加密的非加密改编。它的周期为 2 514 (2 256 个流,长度为 2 258 )。
7)shr3cong
Marsaglia 的 SHR3 移位寄存器生成器与线性同余生成器求和,其中乘数为 a = 69069,加数为b = 1234567 ,模为 2 −32 。SHR3 是一个定义为 u = u ( I + L 13 )( I + R 17 )( I + L 5 ) 的 3 移位寄存器生成器,其中 I 为单位运算符, L 为向左移位运算符, R 为向右移位运算符。此组合生成器(SHR3 部分在[7] 中有述)的周期约为 2 64。此生成器不支持多个流或子流。每个 U(0,1) 值都是使用一个 32 位整数通过该生成器创建的;可能的值为 2 −32 的所有倍数(严格位于区间 (0, 1) 内)。默认情况下用于shr3cong 流的 randn 算法为早期形式的 ziggurat 算法 [9],但基于 shr3cong 生成器。此生成器与 randn 函数从 MATLAB 版本 5 开始使用的生成器相同,通过 randn('state',s) 进行激活。
注意 [6] (1999) 中用到的 SHR3 生成器与 [7] (2000) 中不同。MATLAB 使用 [7] 中提供的最新版生成器。
8)swb2712
修正的借位减法生成器,如[8]中所述。此生成器与加法滞后 Fibonacci 生成器(其滞后值为 27 和12)类似,但修改后具有约为 2 1492 的更长周期。此生成器本身会使用双精度类型来创建 U(0,1) 值,并且开区间 (0, 1) 中的所有值都是可能的。默认情况下用于 swb2712 流的 randn 算法为 ziggurat算法 [7],但基于 swb2712 生成器。
注意 此生成器与 rand 函数从 MATLAB 版本 5 开始使用的生成器相同,通过 rand('state',s) 进行激活。
4.4转换算法
1)Inversion
通过对均匀的随机变量应用标准正态逆累积分布函数来计算正态随机变量。每个正态值恰好使用一个均匀值。
2)Polar
极坐标抑制算法,如[1]中所述。每个正态值平均约使用 1.27 个均匀值。
3)Ziggurat
ziggurat 算法,如[7]中所述。每个正态值平均约使用 2.02 个均匀值。
4.5配置流
随机数流 s 具有可控制其行为的属性。要访问或更改属性,请使用语法 p = s.Property 和 s.Property = p。例如,当使用 randn 时,您可以配置转换算法以生成正态分布的伪随机值。使用默认的 Ziggurat 转换算法生成正态分布的伪随机值。
s1 = RandStream( 'mt19937ar' );
s1.NormalTransform
ans = 'Ziggurat'
r1 = randn(s1,1,10);
将流配置为使用 Polar 转换算法来生成正态分布的伪随机值。
s1.NormalTransform = 'Polar'
s1 =
mt19937ar random stream
Seed: 0
NormalTransform: Polar
r2 = randn(s1,1,10);
当使用 rand 生成均匀分布的随机数时,您还可以配置流以生成对偶伪随机值,即从 1 减去生成的随机数得到。从流 s 中创建 6 个均匀分布的随机数。
s2 = RandStream( 'mt19937ar' );
r1 = rand(s2,1,6)
r1 =
0.8147 0.9058 0.1270 0.9134 0.6324 0.0975
还原流的初始状态。在 Antithetic 属性设置为 true 的状态下创建另外 6 个随机数。检查这 6 个随机数是否等于先前生成的从 1 减去的随机数。
reset(s2)
s2.Antithetic = true;
r2 = rand(s2,1,6)
r2 =
0.1853 0.0942 0.8730 0.0866 0.3676 0.9025
isequal(r1,1 - r2)
ans =
1
您可以分别使用 A = get(s) 和 set(s,A) 来保存和还原流 s 的所有属性,而不是逐个设置流的属性。例如,将流 s2 的所有属性配置为与流 s1 相同。
A = get(s1)
A =
Type: 'mt19937ar'
NumStreams: 1
StreamIndex: 1
Substream: 1
Seed: 0
State: [625x1 uint32]
NormalTransform: 'Polar'
Antithetic: 0
FullPrecision: 1
set(s2,A)
Type: 'mt19937ar'
NumStreams: 1
StreamIndex: 1
Substream: 1
Seed: 0
State: [625x1 uint32]
NormalTransform: 'Polar'
Antithetic: 0
FullPrecision: 1
get 和 set 函数使您能够保存和还原流的整个配置,以便稍后可以准确地重现结果。
4.6还原随机数生成器的状态以重现输出
State 属性是随机数生成器的内部状态。当生成随机数时,您可以在仿真的某个点上保存全局流的状态,以便稍后重现结果。
使用 RandStream.getGlobalStream 返回全局流的句柄,即 rand 从中生成随机数的当前全局流。保存全局流的状态。
globalStream = RandStream.getGlobalStream;
myState = globalStream.State;
使用 myState ,可以恢复 globalStream 的状态并重新生成以前的结果。
A = rand(1,100);
globalStream.State = myState;
B = rand(1,100);
isequal(A,B)
ans = logical
1
rand、 randi 、 randn 和 randperm 访问全局流。由于所有这些函数都访问相同的基础流,因此调用其中一个函数会影响其他函数在后续调用时生成的值。
globalStream.State = myState;
A = rand(1,100);
globalStream.State = myState;
C = randi(100);
B = rand(1,100);
isequal(A,B)
ans = logical
0
您也可以使用 reset 函数将流重置为其初始设置。
reset(globalStream)
A = rand(1,100);
reset(globalStream)
B = rand(1,100);
isequal(A,B)
ans = logical
1