Pytorch的CNN,RNN&LSTM
CNN
拿二维卷积举例,我们先来看参数

卷积的基本原理,默认你已经知道了,然后我们来解释pytorch的各个参数,以及其背后的计算过程。
首先我们先来看卷积过后图片的形状的计算:
参数:
kernel_size :卷积核的大小,可以是一个元组,也就是(行大小,列大小)
stride : 移动步长,同样的可以是一个元组
padding:填充,同样的可以是一个元组。注意,填充是两边都填,如果原本宽是x,填充1后,宽会变成x+2,因为左右都填充了1
dilation : 空洞卷积大小
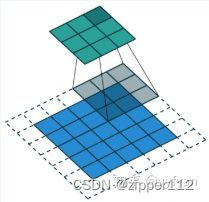
空洞卷积:
这里解释一下dilation,你可以认为他就是把卷积核之间加了一些洞,在不改变参数量的情况下增加了感受野。
下面两张图片引用自下面的链接,想详细了解空洞卷积的,可以看这篇文章。
https://zhuanlan.zhihu.com/p/50369448
dilation=1,此时卷积核的每个参数都是相邻的
dilation=2,此时卷积核的每个参数和上下左右都有一个空隙,这个空隙是一种间隔并不是一种参数,所以从形式上来看,卷积核变大变稀疏了,能够捕获更大的范围,但参数量没有变化。
所以,假设原卷积核形状是(a, b)那么dilation=k时,行增加了(k - 1)(a - 1),列增加了(k - 1)(b - 1)。
于是卷积核变成了(a + (k - 1)(a - 1), b + (k - 1)(b - 1))
输出行的计算:
我们来推导行的计算,列的计算同理。
我们可以把行分成两个部分第一个部分是卷积核做的第一次卷积,第二个部分是卷积核向右移动做的卷积。
此时行的大小应该是1 + 向右移动的次数。向右移动的次数应该等于(行大小 - 卷积核宽度) / 步长 再向下取整
行大小 = 图片宽度 + pandding[0] * 2
卷积核宽度 = kernel_size[0] + (dilation[0] - 1)(kernel_size[0] - 1)
我们把卷积核宽度计算展开得到:
卷积核宽度 = dilation[0](kernel_size[0] - 1) + 1
于是把上述公式整合就得到pytorch里的计算式
分组卷积:
我们可以看到Pytorch的CNN里有一个参数叫groups,是为分组卷积做准备的参数。
分组卷积的思路是吧in_channel和out_channel都进行分组,每个组内分别进行卷积运算,最后再把结果进行concat。下面举个例子:
输入in_channel = 4, out_channel = 6, groups = 2。
此时in_channel分成了两组,每组的channel数都是in_channel/groups = 2,同理out_channel 也分成了两组每组的channel数都是out_channel/groups=3
此时输入通道变成了in_channel_groups = (sub_in_channel1=2, sub_in_channel1=2)
输出通道变成了out_channel_groups = (sub_out_channel1=3, sub_out_channel1=3)
我们让sub_in_channel1和sub_out_channel1做卷积,sub_in_channel2和sub_out_channel2做卷积。
最后我们再把两个组的卷积结果concat一下,得到最终结果,第一个组的输出channel数是3,第二个组的数也是3,所以concat之后,输出的通道数还是6.那么,分组卷积的意义何在呢?我们看参数数量就知道了。由于输出通道要除以groups,所以输入通道的数目会减少,此时每一个卷积核要负责的输入通道也就减少了,也就是说,卷积核的参数数目会减少groups倍,这就是分组卷积的意义。
参数量的计算
weight的大小为(out_channel, i n _ c h a n n e l g r o u p s \frac{in\_channel}{groups} groupsin_channel, kernel_size[0], kernel_size[1]),从这里也可以看出groups减少了参数量。
bias的大小就是out_channel的大小了。
示例代码:
conv = torch.nn.Conv2d(in_channels=3, out_channels=3, kernel_size=(3, 3),\
stride=(2, 2), padding=(0, 0), groups=3)
"""
上述代码创建了一个处理3通道图片的卷积层
其中输出通道为3,卷积核形状为(3, 3)没有padding,横向和垂直的步长都是2
输出通道和输入通道都会被平均的分为3组
"""
RNN
同理,这里也默认了你知道了RNN的基础知识,我们来看Pytorch中RNN的官方文档。

这里我们先忽略num_layers, bias, 等参数,先专注于hidden_size和input_size。
先创建一个RNN然后查看参数
rnn = torch.nn.RNN(input_size = 3, hidden_size=5, bias=False)
print(rnn.all_weights)
"""
[[Parameter containing:
tensor([[-0.2646, -0.4045, -0.1925],
[-0.3035, -0.4026, -0.2005],
[ 0.0181, 0.0157, -0.0804],
[ 0.4191, 0.0750, 0.1659],
[ 0.1848, 0.1085, 0.4351]], requires_grad=True), Parameter containing:
tensor([[ 0.4092, 0.1956, -0.1648, 0.0278, -0.3483],
[ 0.3865, 0.3441, 0.1004, -0.4226, -0.2988],
[ 0.2640, 0.3169, -0.2568, -0.3115, 0.3268],
[-0.3311, -0.1856, 0.3827, -0.1265, -0.4149],
[ 0.0930, -0.1986, 0.1813, 0.3944, 0.1576]], requires_grad=True)]]
"""
可以看到有两个参数,一个是wi=(5, 3)一个是wh=(5, 5),第一个参数wi用于乘以输入的数据,而第二个参数wh用于和隐藏层的向量相乘,在结合官方给出的RNN计算,我们就可以手动模拟以下RNN的推理过程了,RNN有两个输出,一个是out_put,一个是h_0
手动模拟:
data = torch.randn(size=(2, 4, 3), dtype=torch.float32) # 输入的数据 rnn = torch.nn.RNN(input_size = 3, hidden_size=5, bias=False) wh = rnn.all_weights[0][0] wi = rnn.all_weights[0][1] h0 = torch.zeros(size=(1, 4, 5)) up_out = [] # out_put的数据 right_out = None # 隐藏层最终输出 acfun = torch.nn.Tanh() for i in range(2): # 2代表时序 tmp1 = data[i].matmul(wh.T) # 计算输入 tmp2 = h0.matmul(wi.T) # 计算隐藏层 res = acfun(tmp1 + tmp2) # 计算新的h_0 up_out.append(res) # 本时刻的输出 h0 = res # 更新隐藏层 print(torch.cat(up_out, dim=0), h0) # 把每一个时刻的输出都concat一下 print(rnn(data))
其余参数:
其余的参数就好理解了,num_layer是控制层数的,这会使得隐藏层增加。Bidirectional是控制是否开双向的最后输出会被叠加在out_put上,batch_first是为了方便输入数据的batch位于第一个维度。
LSTM
LSTM比RNN要复杂很多,同样的,通过模拟LSTM计算的过程,搞清楚pytorch的LSTM是怎么输出的。
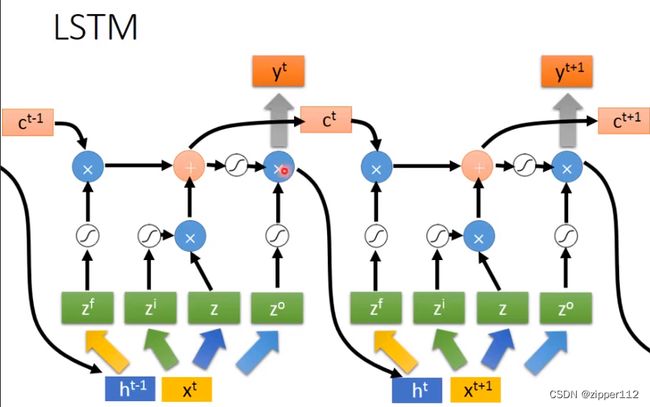
首先先回忆一下LSTM的计算过程:
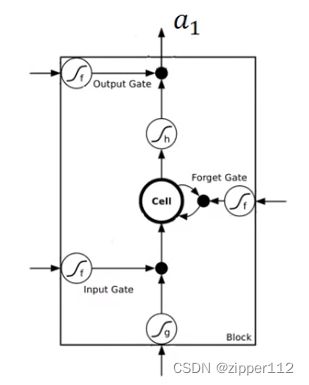
LSTM有三个门,分别是:输入门,输出门,遗忘门。每个门都需要对应一个权重。
除此之外对于输入也还需要做一个做一个变换,所以也需要一个参数。
对于Pytorch的LSTM来说,他还考虑上一次的输出,也就是说,Pytorch的LSTM计算时是这样的
 也可以看到,上一次的输出 h t h_t ht被接到了下一次输入中。那么我们针对于新增的 h t h_t ht也需要对应的参数。
也可以看到,上一次的输出 h t h_t ht被接到了下一次输入中。那么我们针对于新增的 h t h_t ht也需要对应的参数。
那么Pytorch的LSTM一共有八个参数(除去bias)
观察参数:
首先,对于input_size = a, hidden_size=b的LSTM,针对输入数据的矩阵的形状应该是bxa的。针对上一次输出数据的形状应该是bxb的。
我们来看Pytorch的LSTM的参数rnn = nn.LSTM(input_size = 3, hidden_size=5, bias=False) print(rnn.all_weights[0][0].shape, rnn.all_weights[0][1].shape) """ torch.Size([20, 3]) torch.Size([20, 5]) """我们发现只有两组,其实这是八组。因为针对于输入数据,一共有4个5x3的数据。对于 h t h_t ht一共有4个5x5的数据。为了加快运算,Pytorch把这些数据concat到一起了。于是出现了两个20列的数据。
模拟LSTM运算
根据Pytorch官方给的计算公式和,LSTM的计算图解。我们来进行模拟
首先我们先拆分出来参数wii = rnn.all_weights[0][0][:5, :] wif = rnn.all_weights[0][0][5:10, :] wig = rnn.all_weights[0][0][10:15, :] wio = rnn.all_weights[0][0][15:20, :] whi = rnn.all_weights[0][1][:5, :] whf = rnn.all_weights[0][1][5:10, :] whg = rnn.all_weights[0][1][10:15, :] who = rnn.all_weights[0][1][15:20, :]然后我们把LSTM的三个输入给构造出来
data = torch.randn(size=(2, 4, 3), dtype=torch.float32) h = torch.zeros(size=(1, 4, 5)) # 隐藏层,也就是上一次的输出 c = torch.zeros(size=(1, 4, 5)) # 记忆单元然后我们按照上面的公式进行计算,就会得到最终的结果
import torch
from torch import nn
data = torch.randn(size=(2, 4, 3), dtype=torch.float32)
rnn = nn.LSTM(input_size = 3, hidden_size=5, bias=False)
wii = rnn.all_weights[0][0][:5, :]
wif = rnn.all_weights[0][0][5:10, :]
wig = rnn.all_weights[0][0][10:15, :]
wio = rnn.all_weights[0][0][15:20, :]
whi = rnn.all_weights[0][1][:5, :]
whf = rnn.all_weights[0][1][5:10, :]
whg = rnn.all_weights[0][1][10:15, :]
who = rnn.all_weights[0][1][15:20, :]
h = torch.zeros(size=(1, 4, 5))
c = torch.zeros(size=(1, 4, 5))
up_out = []
tanh = nn.Tanh()
sigmoid = nn.Sigmoid()
for k in range(2):
i = sigmoid(data[k].matmul(wii.T) + h.matmul(whi.T))
f = sigmoid(data[k].matmul(wif.T) + h.matmul(whf.T))
g = tanh(data[k].matmul(wig.T) + h.matmul(whg.T))
o = sigmoid(data[k].matmul(wio.T) + h.matmul(who.T))
c = c * f + i * g
o = tanh(c) * o
up_out.append(o) # 本次的输出加到output中
h = o # 把本次的输出替换h
print(torch.cat(up_out, dim=0), (h, c))
print(rnn(data))
模拟完之后我们就搞懂了Pytorch的LSTM的输入和输出都是啥了:
输入:三个参数,data,隐藏层初始值,记忆单元初始值
输出:两个值,第二个值是一个元组。每一个时刻的输出,隐藏层输出(就是最后一个时刻的输出),记忆单元的值
其余的参数和RNN一致就不再说了