X-volution：统一卷积与自注意力

论文地址：https://arxiv.org/pdf/2106.02253.pdf

目录

1、动机

2、方法

2.1、卷积模块

2.2、自注意力模块

2.3、全局自注意力的近似

2.4、卷积与自注意力的统一：X-volution

2.4.1、卷积与自注意力的互补

2.4.2、多分支拓扑用于训练阶段

2.4.3、合并多分支用于推理阶段

3、实验结果

---

1、动机

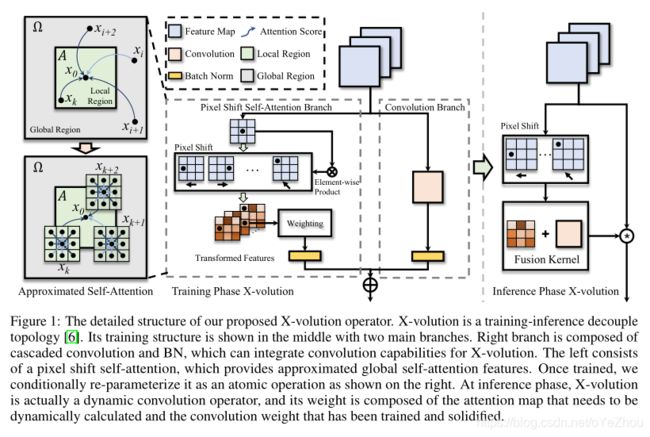
卷积和注意力是DNN中的两种基本构造块，前者可以提取图像的局部特征，后者可以非局部编码高阶的上下文关系。这两者原则上是可以互补的，不过目前还没有在同一个模块中兼具两者优点的方法。于是，本文提出了一个X-volution模块，对这两者进行了统一，使得模块兼具CNN的局部特征提取能力和注意力的全局建模能力。在本文中，作者从理论上推导了一种全局自注意力的近似进制，使用卷积来逼近自注意力。基于这种近似机制，建立了一个由卷积和自注意操作组成的多分支元模块，能够统一局部和非局部特征交互。

更重要的是，利用结构重参数化思想可以类似于RepVGG那样，将训练-推理解耦，在训练之后转换为一个卷积类型的操作符，因此能够插入到任何当代网络中。

2、方法

2.1、卷积模块

卷积通过在有限的局部区域内线性加权得到输出，对于输入，其输出为，则卷积操作可以定义为：

  （1）

公式（1）表明：卷积实际上是一种线性加权操作。

2.2、自注意力模块

自注意力通过执行向量内积来建模长期语义互补。与卷积不同的是，自注意力不直接对输入tensor进行操作，而是先将其转换为Query、Key、Value三个tensor，形式都是。然后使用如下方式计算：

  （2）

其中，表示自注意力的相关矩阵。公式（2）表明，自注意力是一种高阶的全局操作。

2.3、全局自注意力的近似

全局自注意力是最为原始的注意力机制，其有效性源自其全局性。然而，其计算复杂度非常高（平方级），这就限制了其实际使用。那么，关键问题就成了能否找到一个公式（2）中的近似，也即：能否找到的一个使用离线操作（卷积、点乘）的替代。

作者通过简单地逐元素位移和点乘操作，以卷积的形式近似了全局注意力。给定特征tensor X，定义其特征向量为，其注意力可以表示为：

  （3）

其中，，表示全局区域，A表示上的局部区域。

作者将其分为了局部区域和非局部区域，如图1左侧所示：灰色区域为全局区域，绿色box为局部区域；此外，局部区域之外的部分，为非局部区域。

由于图像具备很强的马尔科夫性质，可以近似的由其局部区域的像素线性表示：，其中表示线性权重。那么，公式（3）的第二项可以表示为：

  （4）

在不失去一般性的情况下，我们可以在区域A中加入系数为零的项。通过设计，非局部区域也在局部区域的边界像素的接受域内。因此，我们可以将公式（4）转化为:

  （5）

根据图像的马尔可夫性质，我们可以假设对于x k∈A, xi(远离x k)与x k之间的相互作用是弱的。因此，可以进一步简化式5:

  （6）

将式（6）带入带式（3），可得：

  （7）

因此，在处的全局注意力可以通过其邻域像素的注意力加权求和来近似。基于上述理解，可以设计一种逐点的上下文传播来估计全局注意力。作者提出了一个全局注意力近似方案，Pixel Shift Self-Attention(PSSA)，基于像素偏移和卷积来近似全局注意。

具体来说：

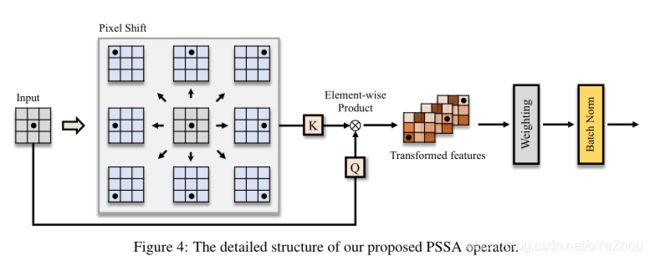
• 首先对feature map沿着给定的方向（左、右、上、下）移动L个像素；
• 然后对原始特征和位移后的特征进行逐元素乘积，得到转换特征，实际上，移位积操作建立了邻域内点之间的上下文关系，通过分层叠加，我们可以将上下文关系传播到全局区域；
• 最后，我们对这些变换后的特征进行加权求和(可以通过卷积算子实现)，得到一个近似的自注意力映射。

平移、元素积和加权求和的复杂度为O(n)，因此提出的PSSA是一个时间复杂度为O(n)的算子。值得注意的是，PSSA事实上就是利用转换特征将self-attention变成了一个标准卷积操作，然后经过层次堆叠，这种结构就可以通过上下文信息的传播实现全局注意力。

PSSA的具体结构，如图4所示：

2.4、卷积与自注意力的统一：X-volution

2.4.1、卷积与自注意力的互补

卷积的局部性和各向同性的归纳偏置，赋予其平移等变性的能力。但也正是由于其局部性质，使得其不能建立长期依赖关系，这对图灵完备算子来说又是必不可少的。与卷积相反，自注意力放弃了上面所说的归纳偏置，也即所谓的low-bias，力求在没有明确模型假设的情况下从数据集中发现自然模式。这种low-bias准则使得自注意力能够自由探索复杂的关系（如：长期依赖、各向同性的语义、CNNs中的强局部相关等）。正因为其学习的自由度较高，所以需要大规模的数据集来预训练，且优化难度较大，需要使用较长的训练周期以及复杂tricks。

鉴于卷积和自注意力各自的优缺点，有些研究（AANet、CVT）就提出卷积应该和自注意力结合起来，以提高鲁棒性与性能。也即：利用不同的模型假设，使卷积和自我注意在优化特征(即良好/病态)、注意范围(即局部/长期)和内容依赖(内容依赖/独立)等方面相互补充。

2.4.2、多分支拓扑用于训练阶段

也有一些研究试图将卷积和自注意力结合起来，不过这种结合比较粗糙，不能组合成一个原子操作。如AANet直接将卷积层和自注意力层的结果拼接起来，以获取合并后的结果，但也表明了如果使用单一的卷积或者单一的自注意力，会导致性能下降，只有同时存在两种操作才会提升性能。

本文提出了一种多分支的拓扑结构，将卷积和自注意力操作通过这种结构来组合起来，如图1中间部分所示。该分支分为两部分：左边分支由像素位移自注意力和BN组成，用于近似全局自注意力操作；右边分支被设计为卷积分支，由级联的卷积和BN组成。

2.4.3、合并多分支用于推理阶段

多分支结构能够使卷积和自注意力相结合，从而提升性能。但是，这种组合仍然不能视为一个原子操作。因此，难以进行高效的推理。而单个原子操作效率更高，内存开销更低，这是硬件友好的。

因此，这里对训练与推理过程的网络结构进行解耦，在训练时保持多分支结构，而推理时则通过结构重参数化将其转换为单分支结构。

对于多分支训练过程：

  (8)

可以表示为：

  （9）

可见，可以将多分支转换为单分支，从而形成一个原子操作，称作X-volution，具体如上面的图1右侧所示。

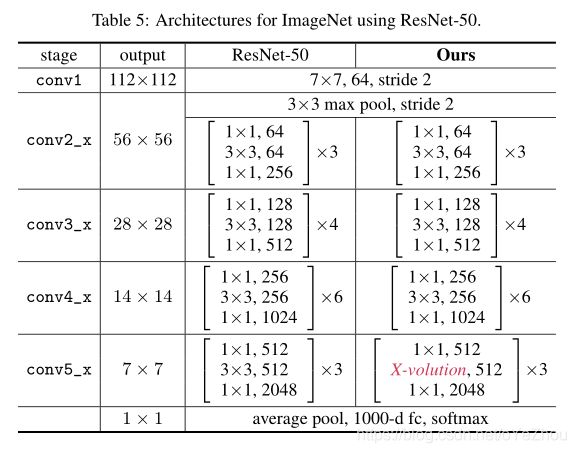
值得注意的是，这种原子操作可以插入到主流的网络（如ResNet等）中：

3、实验结果