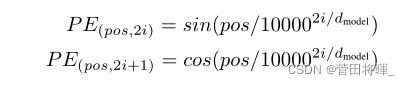Transformer(“变形金刚”)
上一篇博客里面,我们讲解了self-attention机制。而self-attention机制最早是在“Attenion Is All Your Need”这篇论文中提出的。而self-attention只不过是这边论文的很小一支而已。所以今天在这里我们要介绍这篇论文的精髓所在——Transformer(“变形金刚”)
1.Transformer模型结构
在第一次写attention那篇博客中,我们将attention机制嵌套到了Encode—Decoder的架构来解释其运行的原理。在那篇博客中,我们利用Lstm来作为Encoder和Decoder。而在这篇文章中,同样如此,self-attention也是嵌套在Encoder和Decoder中,只不过在这里Transformer的Encoder和Decoder是使用纯注意力机制。
上图所展示的便是Transformer的结构图。
从上图我们可以看到Transformer共有两个部分,左边的部分是Transformer的Encoder,右边的部分是Transformer的Decoder。
1.1Transformer—Encoder
从Encoder和Decoder的结构来看,Encoder—layer只比Decoder—layer少一个部分,相较简单,因此我们这里先介绍Encoder。
从上图我们可以看到,Encoder由N个layer组成,形成一个整体。而每一个Encoder—layer又是由两个部分组成的(在这里我们将每一个部分叫做一个sub_layer)。这里我们稍微来解释一下每一个小模块在干什么。
(1)Multi-Head Attention:多头自注意力层,输出的结果与输入相关(参考self-attention输出的b1)
(2)Add&Norm:残差归一层(我自称),做残差操作并对得到的结果做layer normalization(区别于batch normalization)
(3)Feed Forward:一个基于位置的前馈全连接层,提供非线性变换。
因此简单知道了每个层的作用以后,我们便可以用公式表示他们之间的关系。
上图所展示的便是Encoder—layer的公式。
1.2 Transformer—Decoder
解释完了Encoder的相关结构,我们这里来看下Decoder的结构。从上图我们可以看到,Decoder由N个layer组成,形成一个整体。而每一Decoder—layer又是由三个部分组成的(在这里我们将个每一个部分叫做一个sub_layer)。我们已经在Encoder中解释了其中的两个,不再做解释。
(1)Masked multi-head attention:有掩码的多头注意力,Decoder对t时刻的x输入,遮住t时刻以后的元素,只考虑t时刻之前。(确保预测第t个位置时不会接触到t+1以后的信息。)
介绍完所有的Encoder和Decoder的sub_layer以后,我们便可以大概的知道了,这个Transformer他具体在做什么事儿了。
首先是我们inputs X(source)输入到Transformer的Encoder中。对于Decoder输入的部分,如果是第一个输入,我们会输入一个
2.Transformer实现
介绍了Transformer模型大致的结构以后,我们对模型也有了一个大致的了解。但对于每一个Encoder,Decoder的具体模块的实现我们还不是很了解,这里我们就一一来打开这些黑盒子。(这些黑盒子也是我本人在学习过程中比较不理解的地方,也欢迎大家来讨论。)
2.1 Multi-Head Attention
多头注意力机制类似于单头的注意力机制,只不过在原来一个Q,K,V的地方又多加了几个,最后再通过线性映射将其进行整合。
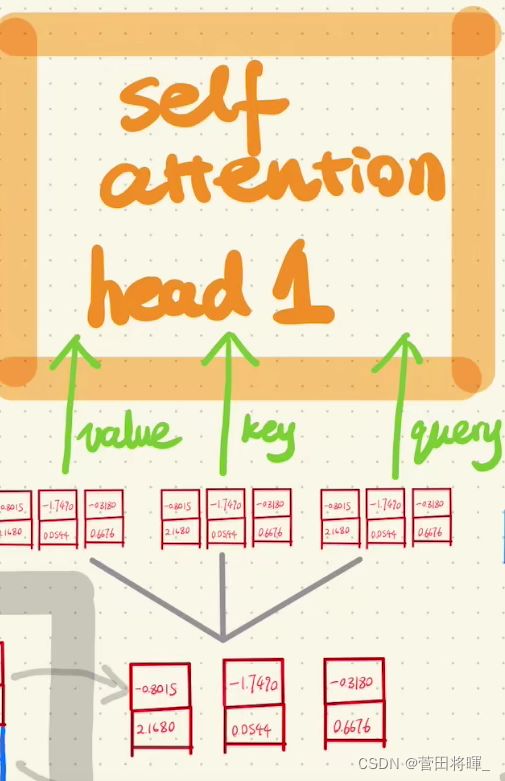
上图所展示的便是Multi-Head Attention的输入。
首先,我们将positional embeding的输出分成三份,作为Q,K,V作为Multi-Head Attention的输入。
上图所展示的便是Multi-Head Attention的结构图
首先我们会将输入的Q,K,V进入其对应的线性层,乘上对应的可学习的参数矩阵,从而得到Q—_,K_,V_。
上图所展示的便是Multi-Head Attention线性层的运算
Tip:这里图中的W有错误,图中为2乘以2,实则是2乘以1,因为最后多头的输出会整合,所以有问题。
随后我们便可以将输出的Q_,K_,V_输入到attention层中。
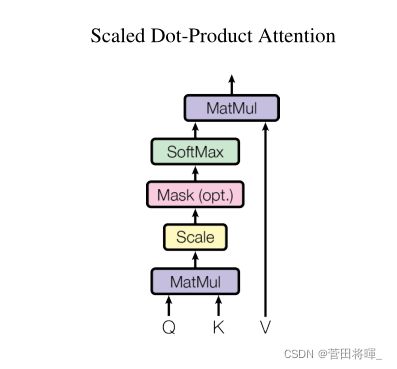
上图所展示的便是Multi-Head Attention中的attention层的结构
从上图所展示的是attention层中一个头的计算(其他头的计算都是一样的。)
上图所展示的便是Multi-Head Attention中的attention层的具体计算及其对应的公式。
这边我们再来讲一下scale和mask模块。scale这里原文是除以根号512,其目的为了减少值与值之间的相对差距(避免大的太大,小的太小),而mask模块这里是用在Decoder中。(确保预测第t个位置时不会接触到t+1以后的信息。)
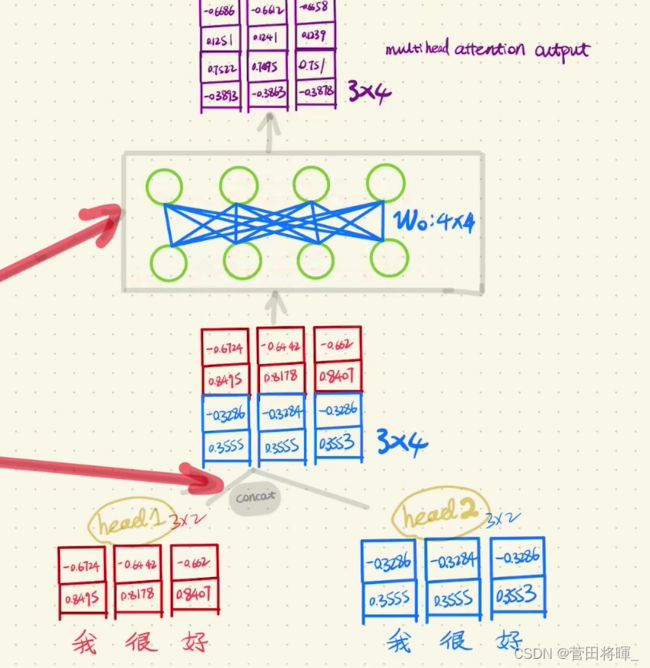
得到多头计算的输出后,我们便会将每一个头的结果进行一个整合,最后经过一个线性层得到我们最后的结果。
上图所展示的便是Multi-Head Attention最后的输出
2.2 layer normalization
layer normalization的意思就是对你输入的向量的每一层做归一化。我们先来解释一下 layer normalization和batch normalization。
首先我们以二维向量输入为例。
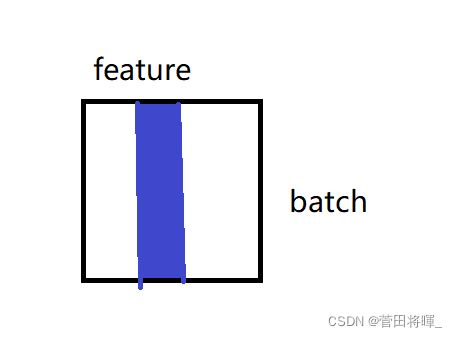
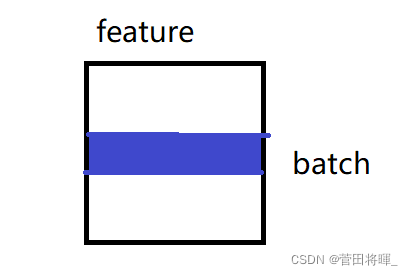
上图所展示的便是batch normalization运算图。
从上图我们可以看到batch normalization做的是将每一个feature做归一(均值为0,方差为1的数)
上图所展示的便是layer normalization运算图。
相反,从上图我们可以看到layer normalization做的是将每一个样本做归一(均值为0,方差为1的数)
理解了二维向量的归一,我们这里便可以知道三维的向量的归一了。
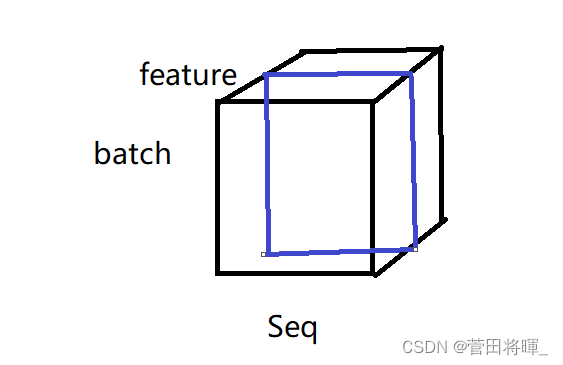
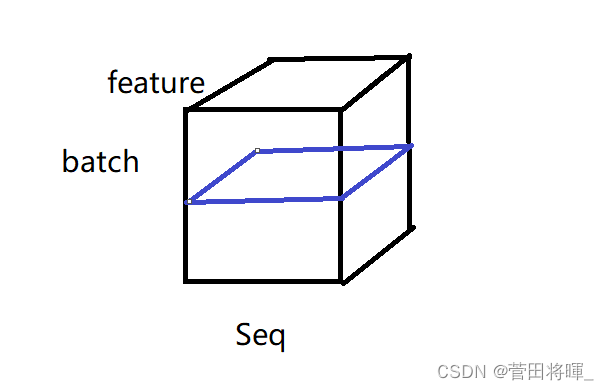
上图所展示的分别为batch normalization和layer normalization运算图。
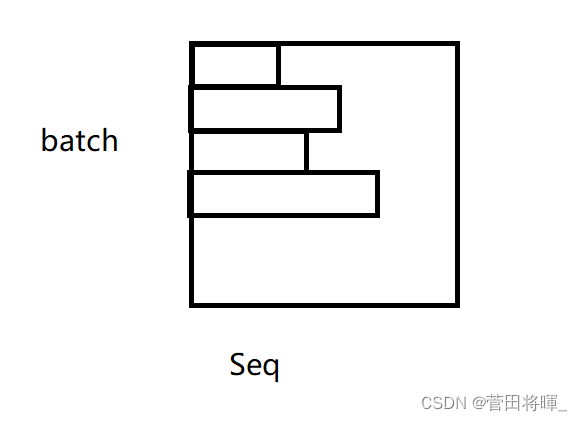
我们知道,对于语义的输入,每一个batch中的Seq的大小并不是相同的。它们又句子长,有的句子短,所以如果在这里做batch normalization的话,则会导致每一次计算mini-batch的均值和方差相对来说抖动会比较大。但如果说用layer normalization来做的话,他每次都是对每一个句子进行一个归一,因此会比batch normalization相对的稳定一些。
上图所展示的便是输入序列长度不同时的情况。
2.3 Positional Encoding
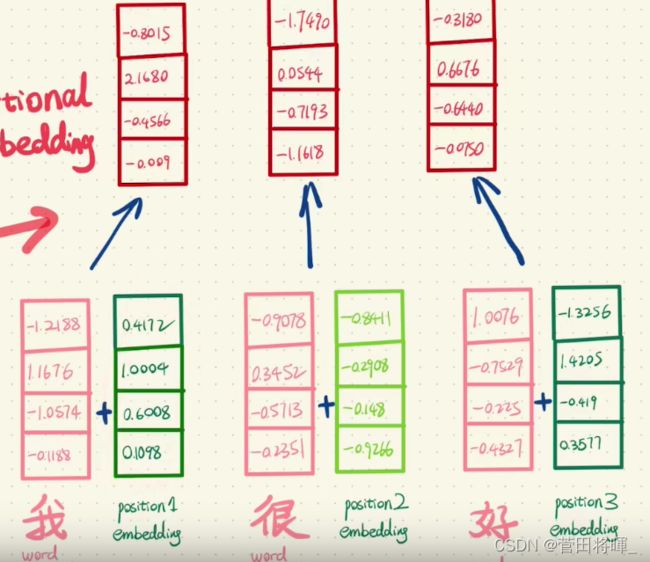
Positional Encoding翻译过来是位置编码的意思。顾名思义Positional Encoding的意思就是对每一个所输出的词给予对应的位置信息。
就如我们上面介绍的,Transformer的Encoder和Decoder是注意机制的,所以为了让模型知道词序的信息,我们这里加入了位置编码。
在原文中,作者利用三角函数分别为奇数位和偶数位加入了位置编码。(这里有涉及傅里叶变换的原因所以就不仔细深究了)
上图所展示的便是Positional Encoding运算图。