勘探开发人工智能技术:机器学习(1)
0 提纲
2.1 什么是机器学习
2.2 不确定性
2.3 数据类型
2.4 分类、回归、聚类
2.5 分类问题的训练与测试
2.6 性能评价指标
1 什么是机器学习
对于西瓜这个抽象类来说,它具有“色泽”,“根蒂”,“敲声”三个属性:

通过观察这个简单的由四个西瓜组成的数据集,可以得到如下假设:
- “敲声=浊响”的西瓜是好瓜;
- “根蒂=蜷缩”的西瓜是好瓜;
- “敲声=浊响”并且“根蒂=蜷缩”的西瓜是好瓜。
这是我们人为逻辑推理得到的假设,这些假设就是机器学习需要学到的**“模型(model)”**。
如果想让机器去“学习”这些假设,该怎么做?最基本的想法是为机器提供所有的假设,对每个假设进行验证,一旦发现不符合数据的假设,就剔除。
-
构建假设空间:假设“色泽”、“根蒂”、“敲声”分别有2、3、3种可能取值,同时还要考虑可以取任意值,比如无论色泽如何,“敲声=浊响”并且“根蒂=蜷缩”的西瓜是好瓜,所以共产生3 × 4 × 4 = 48种假设。西瓜问题的假设空间如下:

- 2.色泽= * 根蒂 = * 敲声 = 浊响
- 5.色泽=* 根蒂=蜷缩 敲声=*
- 6.色泽=* 根蒂=蜷缩 敲声=浊响

机器学习是一类算法的总称,是从大量历史数据或以往的经验中挖掘出隐含的规律,用于预测或者分类。
机器学习可以看作是寻找一个函数,输入是样本数据,输出是期望的结果,只是这个函数过于复杂,以至于不太方便形式化表达。
需要注意的是,机器学习的目标是使学到的函数很好地适用于“新样本”,而不仅仅是在训练样本上表现很好。学到的函数适用于新样本的能力,称为泛化(Generalization)能力。
机器学习的研究方向:
- 传统机器学习的研究:主要包括决策树、随机森林、人工神经网络、贝叶斯学习等方面的研究;
- 大数据环境下机器学习的研究:大数据时代,数据的体量有了前所未有的增长。如何基于机器学习对复杂多样的数据进行深层次的分析,更高效地利用信息,成为当前大数据环境下机器学习研究的主要方向。
机器学习的类型,基于学习方式的分类:
- 监督学习:输入数据中有“导师”;
- 无监督学习:输入数据中无“导师”,采用聚类方法,学习结果为类别。典型的无监督学习有发现学习、聚类分析、竞争学习等;
- 半监督学习:输入数据中有的数据有标签,有的数据没有标签;
- 强化学习:以环境反馈(奖/惩信号)作为输入,以统计和动态规划技术作为指导的一种学习方法。算法根据当前的环境状态确定下一个动作,目标是让得到的收益最大化。
机器学习的类型,基于数据形式的分类:
- 结构化学习:以结构化数据为输入,以数值计算或符号推演为方法。典型的结构化学习有神经网络学习、统计学习、决策树学习、规则学习。
- 非结构化学习:以非结构化数据为输入,典型的非结构化学习有类比学习、案例学习、解释学习、文本挖掘、图像挖掘、Web 挖掘等。
2 机器学习:不确定性
机器学习不保证 100% 的准确性.
2.1 确定性
机器学习一般用于解决不确定性问题.
现实生活中确定性的例子:
- 已知我的工作量, 求我本月的收入 (财务处不会搞错);
- 已知我的各科成绩, 求总分 (老师不会搞错);
- 已知二哈撕了沙发, 求它是否将拥有完整的汪生 (主人不会惯着)。
2.2 不确定性
现实生活有更多不确定性的例子:
- 如果我去向那个女生表白, 她会同意吗? (Y/N)
- 哪个国家会夺得下届奥运会团体射击冠军? (中国队/美国队/法国队/…)
- 根据一张照片判断人的年龄. ([0 , 100])
- 根据某只股票这段时间的价格波动, 判断明天的涨/跌. ([−10%,+10%])
- 明天的天气如何? (有雨/无雨, 有风/无风, 有太阳/无太阳, …)
- 把一大堆照片分成若干小堆, 怎么分最好?
所谓不确定性, 是指我们在进行预测的时候, 不能够保证 100% 的准确.
- 机器学习的本质, 就是 “猜”, 谁猜得更好, 谁就赢了.
- 机器学习有时也做一些确定性问题. 但这些问题的复杂度过高, 求最优解从计算上来说不可行 (一般是 NP 难问题之类), 所以使用启发式算法之类求次优解.
不确定性产生的原因:
- 信息不足. 按理说那个女生要答应我的, 但我不知道她刚挂科心情不好, 贸然行动导致被拒. 只考虑股价而不关心政策的变化, 注定要被深度套牢.
- 噪音. 照片太模糊, 粉丝都无法区分是张曼玉还是王祖贤。
3 机器学习:数据类型
当前机器学习能处理的 (输入) 数据包括结构化数据、序列、图片、图等等.
3.1 基本数据元素类型
基本数据元素 (data item) 的类型:布尔型、枚举型、实型等。
- 布尔型有两种取值, 如: Yes/No, Pass/Fail.
- 枚举型有多种取值, 如: 颜色有红/黄/绿, 形状有方/圆/梯. 这些值之间一般没有大小关系.
- 实型如: 人的身高, 体重. 简便起见整型一般也当成实型, 而不是枚举型来处理.
3.2 其它类型
结构化数据是指每个实例/instance (样本/sample)用同一组特征/feature (属性/attribute) 进行描述.
- 例: 每个就诊者的检测报告包括: 性别、年龄、血压、红细胞数量、血小板数量共 5 个特征.
- 某些机器学习方法 (如决策树) 处理枚举型数据; 有些方法则只处理实型数据, 这时一个实例可以表示为一个向量.
- 如果数据的特征既有枚举型的, 又有实型的 (或其它类型), 就可以称为 异构数据 (heterogeneous data).
图像数据本身可以用一个矩阵来表示.
序列数据由枚举型或实型组成.
视频数据则是图像组成的序列数据.
图数据是指数据用结点和边表示. 如社交网络中, 结点表示人 (有性别、学历等特征), 边表示人与人之间的关系 (父女, 朋友等).
4 机器学习:分类、回归、聚类
分类与回归具有不同的预测数据类型, 聚类本身没有标签.
4.1 分类
数据类型从输入数据的角度来进行讨论, 这里从输出数据, 或者目标的角度来讨论.
分类是指将一个样本预测为给定类别之一. 也称为该样本打标签.
- 例 1: 如果我去向那个女生表白, 她会同意吗? (Y/N)
- 由于可能的类别只有两种, 这被称为二分类问题;
- 例 2: 哪个国家会夺得下届奥运会团体射击冠军? (中国队/美国队/法国队/…)
- 由于可能的类别有多种, 这被称为多分类问题.
多标签分类是指类别之间没有互斥性.
- 例 3: 明天的天气如何? (有雨/无雨, 有风/无风, 有太阳/无太阳, …) 明天可以既刮风又下雨, 甚至边下雨边出太阳.
4.2 回归
回归是指为一个输出为实型值的预测.
- 例 4: 根据一张照片判断人的年龄. ([0,100])
- 由于人的年龄是实型 (虽然这里是整型, 但它的值可以比较大小, 也可以当成实型对待)
- 例 5: 根据某只股票这段时间的价格波动, 判断明天的涨/跌. ([−10%,+10%])
- 由于它的输入数据是前面若干天的数据, 而不是当天的数据, 这被称为时序回归问题.
4.3 聚类
聚类是指根据样本的属性, 把给定的样本集合划分为若干个子集.
- 例 6: 把一大堆照片分成若干小堆. 如果能够获得关于这个划分良好的解释更好.
- 聚类与分类 (回归) 之间存在本质的区别, 它进行新样本的预测. 这是迫不得已的事情, 因为很多数据并没有人类先给的标签, 导致缺乏一个确定的目标, 机器只有根据自己理解来划分.
5 机器学习:分类问题的训练与测试
训练是做题, 验证是小考, 测试是高考, 高考成绩好的学生被选拔出来.
5.1 基本概念
上午来了 60 个患者, 根据他们的各项检测指标 (即数据), 主治医生给出了诊断结论 (如是否患病, 以及患哪种病), 但不会告诉实习生诊断的方法.
实习生根据这 60 条数据, 归纳总结出了诊断模型 (方法), 这是一个从数据中学习的过程.
下午来了 40 个患者, 根据他们的各项检测指标, 以及自己的诊断模型, 实习生给出了诊断结论.
主治医生比对实习生的结论与标准答案, 对实习生的学习能力进行评价. 例如, 实习生弄错了 5 个, 则其错误率为 5/40 = 12.5%, 准确率则为 87.5%.
- 上午 60 条数据是主治医生给定的, 因此称为训练集(split-in-two).
- 下午 40 条数据是用于考实习生的, 因此称为测试集(split-in-two).
- 让计算机作为实习生, 就称为机器学习.
- 由于主治医生 (supervisor) 给定了训练集的所有标签, 因此称为监督学习 (supervised learning).
5.2 训练、测试的不同方案
不同学习方法可能对于不同的训练数据的适应性也不同, 例如, 使用 1-60 号训练, 61-100 号测试的时候, A 学习器优于 B 学习器; 但使用 41-100 号训练, 1-40 号测试的时候, B 优于 A. 为弥补这种数据集划分导致的不公平, 可以使用如下方式:
- 多次随机划分训练集与测试集 (random splitting). 将 split-in-two 重复 10 次, 每次随机进行训练集与测试集的划分. 获得 10 个错误率后, 可以求其均值与方差. 这是论文结果中 82.5 ±0.4 这类准确率的来历.
- 交叉验证 (cross validation). 数据集中有 100 条数据. 将其分为 5 份, 即每份 20 条数据. 每次选择其中 4 份 (即 80 数据) 进行训练, 其它 1 份 (即 20 条数据) 进行测试. 这样, 所有的数据都被测试过一次. 这种方案被称为 5 折交叉验证 (5 folds cross validation, 5-cv).
- 留一法 (leave-one-out). 这是交叉验证的极端情况. 将数据分为 100 份, 即每份只有一条数据. 这种方式最为公平, 但也最为耗时, 因为要训练-测试 100 次.
- 另一种极端的方案被称为使用训练集进行测试 (use training set). 主治医生给了实习生 100 条带标签的数据, 实习生学习到诊断模型后, 使用它对这同样的100 条数据进行分类. 这也是有意义的.
5.3 拟合能力与泛化能力
当测试集与训练集相同时, 考查的是模型的拟合能力.
很多机器学习模型本质上从输入数据到输出标签的一个函数 (映射). 从理论上讲, 训练的过程, 就是从函数簇中选择对训练数据拟合得最好的那个函数. 从实践上讲, 训练就是构造该函数的过程.
当测试集与训练集不同时, 考查的是模型的泛化能力. 提升泛化能力 (更好地为其他就诊者服务) 才是机器学习的真正目的.
如果实习生在老师教的那些样本上表现非常好, 但在新的样本上表现比较差, 就是产生了 过拟合 (over-fitting).
如何防止过拟合, 适当降低拟合能力以获得更好的泛化能力, 是机器学习的核心.
5.4 验证集
数据集中有 100 条数据. 其中 70 条构成训练集, 20 条作为验证集, 10 条作为测试集. 根据训练集获得一个模型, 在验证集中看效果, 如果不行的话, 就再构建另一个模型, 直到获得满意的模型. 最终仍然在测试集上评估预测模型性能.
可以通过如下例子进行理解:
- 训练集相当于平时的例题, 直接提供标准答案.
- 验证集相当于平时的习题/测验题, 做完题后给你看标准答案.
- 测试集相当于高考题, 只会告诉你考分, 不需要告诉你答案.
5.5 其它说明
测试集仅仅是对模型的预测能力进行一定的评估. 现实生活中, 用于预测的数据, 我们很可能永远得不到标准答案.
回归问题与分类问题同理.
时序回归问题稍有不同. 例如, 使用第 1-100 天的股价, 预测第 101 天的股价; 然后使用第 2-101 天的股价, 预测第 102 天的股价, 以此类推.
基本聚类问题就没有训练/测试的概念.
6 机器学习:性能评价指标
性能评价指标对应于体育项目的评分标准.
6.1 性能评价指标
性能评价是不同方法 PK 的基础. 要清楚裁判的标准, 才能当好一名运动员.
性能评价指标多数时候是比较直观的, 需要足够的合理性, 才能获得大家的认同. 比如, 短跑比拼的是时间, 谁用时少谁就获胜. 如果你制定一个指标, 谁跑的姿式更优美, 就不合适. 当然, 新开发一个项目, 跳健美操, 就是比姿式了.
有些人专门研究性能评价指标, 很有意义. 但相应的论文不多, 毕竟项目的个数要远远少于运动员的人数.
6.2 分类问题评价指标
准确率 Accuracy:100 个测试样本, 预测正确 95 个, 则准确率为 95%.
- 如果是二分类问题, 准确率低于 50% 毫无意义.
- 如果是多分类问题, 准确率低于 50% 也行.
F-measure:对于二分类问题, 我们更关注的可能是其中一类. 如根据症状判断是否流感. 将就诊者称为样本, 患流感称为正例, 否则为负例.
- 实际的正例有 15 + 5 = 20 个; 实际的负例有 20 + 60 = 80 个;
- 本身是正例, 判断正确 (也为正例) 有TP=15 (true positive) 个;
- 本身是正例, 判断错误 (弄成负例) 有FN=5 (false negative) 个;
- 本身是负例, 判断错误 (弄成正例) 有FP=20 (false positive) 个;
- 本身是负例, 判断正确 (也为负例) 有 TN=60 (true negative) 个.
这样可以计算四个评价指标:
- 精度:表示判断为正例的样本中, 有多大比例是正确的. 这适合于推荐系统等应用, 你推荐的电影, 要观众喜欢才行.
P = T P T P + F P = 15 15 + 20 P = \frac{TP}{TP+FP} = \frac{15}{15+20} P=TP+FPTP=15+2015 - 召回率:表示被找出来的样本比例有多大. 这适合于流行病检测等应用, 不要有新冠患者被漏掉.
R = T P T P + F N = 15 15 + 5 R = \frac{TP}{TP+FN} = \frac{15}{15+5} R=TP+FNTP=15+515 - 准确率:针对二分类问题时, 准确率可以写为:
A c c = T P + T N T P + F N + F P + T N = 15 + 60 15 + 5 + 20 + 60 Acc = \frac{TP + TN}{TP+FN+FP+TN} = \frac{15+60}{15+5+20+60} Acc=TP+FN+FP+TNTP+TN=15+5+20+6015+60 - F1-measure: F 1 = 2 ∗ P ∗ R P + R F_1 = \frac{2*P*R}{P +R} F1=P+R2∗P∗R是一个比较综合的评价指标. 当 P = R = 1 P = R = 1 P=R=1时, F 1 = 1 F_1=1 F1=1. 这适合于同时考虑精度与召回率的应用: 如果要精度高, 就尽可能判断样本是负的; 如果要召回率高, 就尽可能判断样本是正的; 而如果要 F 1 F_1 F1高, 则进行了良好的折中.
6.3 ROC曲线
有时候我们并不直接判断某个样本是正是负, 而是给出一些实数值的预测. 例如, 样本 1 为正的可能性为 0.6, 而样本 2 为正的可能性为 0.7. 也就是说, 样本 2 更可能为正. 然后根据设定的阈值来判断是正是负.
- 真阳性率(True Positive Rate,简称TPR):TP/(TP+FN),代表的含义是:实际观测为阳的样本中,模型能够正确识别出来的比例。
- 真阴性率(True Negative Rate,简称TNR):TN/(FP+TN),代表的含义是:实际观测为阴的样本中,模型能够正确识别出来的比例。
- 假阳性率(False Positive Rate,简称FPR):FP/(FP+TN),代表的含义是:实际观测为阴的样本中,被模型错误地划分成阳性的比例。FPR=1-TNR。
我们可以同时使用TPR和FPR来评价一个模型的预测能力。TPR越高、FPR越低,说明模型的预测能力越好。

6.4 从ROC到AUC
除了用于阈值的选择,ROC曲线还可以用于不同模型的比较。下图中有三条 ROC 曲线,A 模型比 B 和 C 都要好。
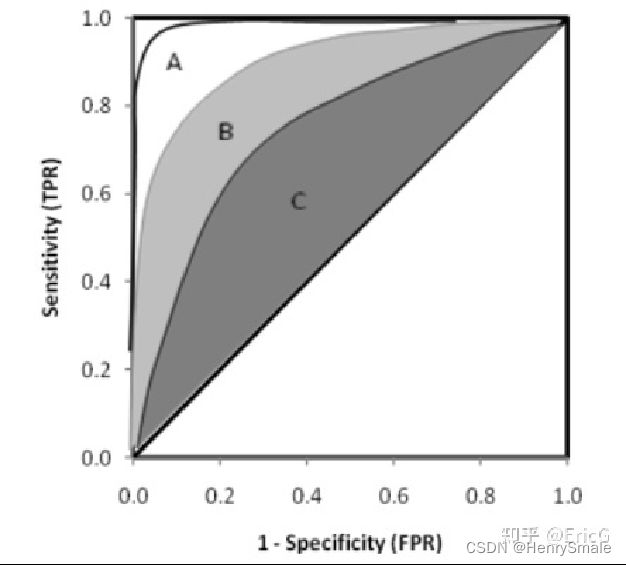
也可以计算出ROC曲线下方的面积,计算出来的面积就是AUC的值了。AUC,即Area Under Curve(ROC曲线下的面积)。

AUC 同样可以用于判断分类器(预测模型)优劣,一般来说,AUC 的值越大越好。
6.5 回归问题评价指标
n n n 个测试样本, 第 i i i 个的真实标签值为 y i y_i yi, 预测标签值为 y i ′ y_i' yi′.
- 平均绝对误差 Mean Absolute Error:
M A E = ∑ i = 1 n ∣ y i − y i ′ ∣ n MAE = \frac{\sum_{i = 1}^{n}|y_i - y_i'|}{n} MAE=n∑i=1n∣yi−yi′∣
错了多少, 就受多大的惩罚 - 均方根误差 Root Mean Squared Error:
R M S E = ∑ i = 1 n ( y i − y i ′ ) 2 n RMSE = \sqrt{\frac{\sum_{i = 1}^{n}(y_i - y_i')^2}{n}} RMSE=n∑i=1n(yi−yi′)2
有一个平方, 导致误差大的预测受到更严厉惩罚
6.6 聚类问题评价指标
聚类没有一个可参考的客观标准, 所以评价指标很凌乱.
- 内部评价指标: 紧密度 (Compactness) 计算每个样本点到它对应的聚类中心的距离, 然后将它们加起来求平均.
- 外部评价指标: 借助于数据的标签. 但这事情比较扯: 数据本身是没有标签的, 聚类结果你爱怎么解释都行, 从逻辑上无法引入客观的一个标签.
关于聚类, 更多指标参见: https://blog.csdn.net/kfnorthwind/article/details/109362011


