[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片
[GAN] 使用GAN网络进行图片生成的“炼丹人”日志——生成向日葵图片
文章目录
- [GAN] 使用GAN网络进行图片生成的“炼丹人”日志——生成向日葵图片
-
- 1. 写在前面:
-
- 1.1 应用场景:
- 1.2 数据集情况:
- 1.3 实验原理讲解和分析(简化版,到时候可以出一期深入的PaperReading)
- 1.4 一些必要的介绍
- 2. 重要实验代码:
-
- 2.1 一些相关的数据预处理
- 2.2 生成器和判别器
- 2.3 损失函数计算
- 2.4 训练和反向传播
- 3. 实验结果分析:
-
- 3.0 baseline
-
- 3.0.1 损失函数:
- 3.0.2 last picture:
- 3.0.3 gif picture:
- 3.1 epoch不变的情况下提高学习率:
-
- 3.1.1 损失函数:
- 3.1.2 last picture:
- 3.1.3 gif picture:
- 3.2 试试增加epoch?:
-
- 3.2.1 损失函数:
- 3.2.2 last picture:
- 3.2.3 gif picture:
- 4. 目前比较不错的效果展示
- 5. 一些其它问题和小小的总结
- 参考资料
1. 写在前面:
1.1 应用场景:
为了支撑人工智能落地,为人们的生活带来更多的便利,充足的数据尤为重要。而在实际的应用中常常会面临专业数据匮乏,数据不均衡的问题,所以利用神经网络根据已有的数据生成新的数据,进行数据扩充,成为了助力人工智能落地的新思路。
1.2 数据集情况:
我所使用的数据集是总量为256张的彩色的向日葵的图片。
1.3 实验原理讲解和分析(简化版,到时候可以出一期深入的PaperReading)
- GAN网络俗称生成式对抗网络,该网络训练了两个模型(即生成器G和判别器D)来进行相互博弈,而博弈的目的是为了得到一个性能较好的可以用于生成我们想要的图片的生成器G。
- 其中生成器网络G是为了生成可以用来迷惑判别器网络D的"假"图像。按数学语言来理解就是要最大化判别器D犯错的概率。
- 而判别器网络D则是为了判别一个样本是不是来自于真实数据。按数学语言来理解就是它用于估计出一个样本是来源于真实的数据而非来自于G的概率。
- 因此,不难得出这个模型的训练的过程大抵就是一个生成器G和判别器D之间的左右互博的过程。
- 不过,值得注意的是这里对G和D的模型的构建使用的是多层感知机MLP(Multilayer perceptrons),也就是在网络上主要是使用全连接层。
- 从这里我们可以看到GAN网络的损失函数为:
- 这个估值函数中由两个部分的数学期望所组成,第一部分是当输入是来自真实样本数据的期望,而第二部分则是当输入是来自生成器生成的样本时的期望。
- 判别器输出的值是一个概率值,这个概率表示输出值是来自真实数据而非来自生成器的程度。
- 这个值越接近1就越表明当前的输入来自真实数据,而越接近0就表示这个输入来自生成器。
- 这样们就可以理解D(x)的目的是为了更好地区分二者,这样能是的D函数输出的值是合理的(更接近1或0)。
- 而G的目的是为了让G(z)更像数据样本,这样可以使得第二个期望中的D(G(z))能被误判为1,这样就可以达到让第二个期望的值尽可能小的效果。
- 再反过来看D的训练,D能更好判别真假,就更加使得第二个期望中的D(G(z))能被正确判为0,这样就可以达到让第二个期望的值尽可能大的效果。
- 所以综合地来看,判别器D就是为了让整个损失(价值)函数尽量大,而生成器则反之,它想让损失函数足够小。这样也就符合我们训练一个网络的指标是让损失值减小,而我们也就可以沿着想办法让损失减小的方向去优化我们的模型从而达到训练出一个较好的生成器。
1.4 一些必要的介绍
- 在我个人的实践中,我所使用的深度学习框架为华为昇腾AI系列的
mindspore-1.9深度学习框架。 - 所使用的笔记本的操作系统为Windows10
- 我使用的是AMD的CPU来进行训练,因为本身该demo的数据量并不是很大。
2. 重要实验代码:
2.1 一些相关的数据预处理
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image # 一个读取图片和对图片做基础操作的类
# 数据转换
image_size = 64
input_images = np.asarray([np.asarray # 将Python的数组转化成npArray
(Image.open(input_data_dir + "/" + file).resize((image_size, image_size)) # 将图片的尺寸转化为 64* 64
.convert("L")) # 将图片转化为灰度图,这样就简化了运算,只需要考虑一个颜色通道了。(可拓展点对RGB三个颜色的通道都进行处理。)
for file in filename])
# 数据预处理
input_images = input_images.reshape(256, 4096) # 将256张图片展平为一维向量
# input_images = input_images.astype('float32')/255 # 把图片的值放缩到(0,1)之间
input_images = (input_images.astype('float32') - 127.5) / 127.5 # 把图片的值放缩到(-1,1)之间
# input_images = (input_images.astype('float32')-mean)/std # 把数据样本转化为均值为0,方差为1的标准化数据(未完成)
2.2 生成器和判别器
# 构建生成器
img_size = 64 # 训练图像长(宽)
class Generator(nn.Cell):
def __init__(self, latent_size, auto_prefix=True):
super(Generator, self).__init__(auto_prefix=auto_prefix)
self.model = nn.SequentialCell()
# [N, 100] -> [N, 128]
# 输入一个100维的0~1之间的高斯分布,然后通过第一层线性变换将其映射到256维
self.model.append(nn.Dense(latent_size, 128))
self.model.append(nn.ReLU())
# [N, 128] -> [N, 256]
self.model.append(nn.Dense(128, 256))
self.model.append(nn.BatchNorm1d(256))
self.model.append(nn.ReLU())
# [N, 256] -> [N, 512]
self.model.append(nn.Dense(256, 512))
self.model.append(nn.BatchNorm1d(512))
self.model.append(nn.ReLU())
# [N, 512] -> [N, 1024]
self.model.append(nn.Dense(512, 1024))
self.model.append(nn.BatchNorm1d(1024))
self.model.append(nn.ReLU())
# [N, 1024] -> [N, 4096]
# 经过线性变换将其变成4096维
self.model.append(nn.Dense(1024, img_size * img_size))
# 经过Tanh激活函数是希望生成的假的图片数据分布能够在-1~1之间
self.model.append(nn.Tanh())
def construct(self, x):
img = self.model(x)
return ops.reshape(img, (-1, 1, 64, 64))
latent_size = 100 # 隐码的长度
net_g = Generator(latent_size)
net_g.update_parameters_name('generator')
# 构建判别器
class Discriminator(nn.Cell):
def __init__(self, auto_prefix=True):
super().__init__(auto_prefix=auto_prefix)
self.model = nn.SequentialCell()
# [N, 4096] -> [N, 1024]
self.model.append(nn.Dense(img_size * img_size, 1024)) # 输入特征数为4096,输出为1024
self.model.append(nn.LeakyReLU()) # 默认斜率为0.2的非线性映射激活函数
# [N, 1024] -> [N, 256]
self.model.append(nn.Dense(1024, 256)) # 进行一个线性映射
self.model.append(nn.LeakyReLU())
# [N, 256] -> [N, 1]
self.model.append(nn.Dense(256, 1))
self.model.append(nn.Sigmoid()) # 二分类激活函数,将实数映射到[0,1]
def construct(self, x):
x_flat = ops.reshape(x, (-1, img_size * img_size))
return self.model(x_flat)
net_d = Discriminator()
net_d.update_parameters_name('discriminator')
2.3 损失函数计算
# 损失函数
adversarial_loss = nn.BCELoss(reduction='mean')
# 损失及梯度计算函数
# 生成器计算损失过程
def generator_forward(test_noises):
fake_data = net_g(test_noises)
fake_out = net_d(fake_data)
loss_g = adversarial_loss(fake_out, ops.ones_like(fake_out))
return loss_g
# 判别器计算损失过程
def discriminator_forward(real_data, test_noises):
fake_data = net_g(test_noises)
fake_out = net_d(fake_data)
real_out = net_d(real_data)
real_loss = adversarial_loss(real_out, ops.ones_like(real_out))
fake_loss = adversarial_loss(fake_out, ops.zeros_like(fake_out))
loss_d = real_loss + fake_loss
return loss_d
2.4 训练和反向传播
def train_step(real_data, latent_code):
# 计算判别器损失和梯度
# 前向计算 => 得到损失函数和梯度参数
# 反向传播 => 使用梯度参数进行权重参数更新
loss_d, grads_d = grad_d(real_data, latent_code)
optimizer_d(grads_d)
loss_g, grads_g = grad_g(latent_code)
optimizer_g(grads_g)
return loss_d, loss_g
3. 实验结果分析:
- 写在前面——在正式进行实验前还有一些随机性的探索。
其中值得一提的是,比起直接把
256张照片一整个当成一个批次epoch来训练的话,在一个epoch内将整个数据集分成几个batch效果会好得多,下面的所有的实验都是在这种情况下进行的训练。
3.0 baseline
- 以下是使用
SGD优化器在学习率lr=0.01并且训练100个epoch后的结果。
3.0.1 损失函数:
3.0.2 last picture:
3.0.3 gif picture:
- 学习率是我们进行超参数调节中非常经常用来调节的一个参数,而
lr=0.01是一个很常用的经验值,所以这次我们就i用这个值来作为一个实验的起始的参考值。- 从上面的损失函数的趋势可以看出,在一个数值比较小的
lr下,损失函数的曲线是相对很平滑的。- 从上面的损失函数的曲线我们也可以看到一个健康的GAN网络训练的过程生成器G的损失和判别器D的损失一般是呈现为在某个区间内相互对峙波动发展的过程。
- 而从上面的结果图来看,现在当前的模型是尚未收敛的状态,需要 “ 去做更多的学习来让自己收敛。 ”
- 那么怎么往下去学得更多呢?
- 我们知道学习的过程是一个反向传播的过程,而控制这个过程的一个重要的参数是学习率,也就是说,我们可以考虑让学习率高一些,这样就可以学得更快一些。
- 从另外一个角度来说我们也可以考虑“学得久一些”,比如增大
epoch看看效果会怎么样? - 而这就是我们本文所研究的两条调参路线。
3.1 epoch不变的情况下提高学习率:
3.1.1 损失函数:
3.1.2 last picture:
3.1.3 gif picture:
- 从上面的部分结果来看的话,在只变动学习率的情况下,对于当前的例子,使用更大的学习率确实能够加速模型的收敛,让生成器最后的效果呈现出一种比较不错的效果,至少整个图片看起来已经是很像一张向日葵的图片。这个是一个不错的进步。
- 但是依然产生了一些新的问题,比如因为学习率变大,虽然收敛的速度变快了,但是损失函数却不是很平滑,充满了各种爆炸的毛刺的气息,这让我想到了过拟合和不稳定。
3.2 试试增加epoch?:
3.2.1 损失函数:
3.2.2 last picture:
3.2.3 gif picture:
- 从最后的效果来看,把epoch增多,最后生成的照片的细腻程度远比
仅有100个epoch的最后的成片的效果好了很多。由此可见,在学习率合理的情况下,去增大训练的epoch量也确实是能比较不错地提升GAN网络最后生成的图片的效果。- 不过也产生了许多新的问题,从上面的这些损失函数可以找到一个共性,那就是
在初期的epoch中,生成器G的损失值是在判别器的损失值的之下的,而随着训练的epoch的量足够大之后,在中后期,会出现判别器D的损失值不断下降,而生成器的损失值则开始上升的情况。这其实直接说明了在这些阶段中继续增大epoch可能并不能很好地朝着我们想要的训练出一个效果更好的生成器的方向演变了。- 从部分实验结果中我们可以发现:
当判别器D的能力相比生成器G更强的时候,G为了能够继续优化,往往就会向模式崩塌的方向走去,它会开始投机取巧,使得最后生成出来的图片会普遍有某种类似,在个性上就不够有好效果了。我们称其为泛化能力不够。
- 这里我以我训练了
500个epoch的一些过程性的截图来展示: SGD优化器,1个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第29张图片](http://img.e-com-net.com/image/info8/612135046ef4443d8761a5dfb8b303d7.jpg)
SGD优化器,50个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第30张图片](http://img.e-com-net.com/image/info8/85b39c24d8ec44ae8f133681cadcaf62.jpg)
SGD优化器,100个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第31张图片](http://img.e-com-net.com/image/info8/4b3d2d6e2a584f828ff55728f2de554f.jpg)
SGD优化器,150个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第32张图片](http://img.e-com-net.com/image/info8/e2c78afe2e0247dc93f0df72a2a36472.jpg)
SGD优化器,200个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第33张图片](http://img.e-com-net.com/image/info8/9337ae892a0d4d04b503852f69689584.jpg)
SGD优化器,250个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第34张图片](http://img.e-com-net.com/image/info8/b658a1b9531d4a67823f53e9d913387c.jpg)
SGD优化器,300个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第35张图片](http://img.e-com-net.com/image/info8/d92165a3da28452891fbfd215b3ecc4b.jpg)
SGD优化器,350个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第36张图片](http://img.e-com-net.com/image/info8/8c53b89fde8d46648e69f1b5e2b9c8fe.jpg)
SGD优化器,400个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第37张图片](http://img.e-com-net.com/image/info8/3507e024625f47fc8c838ec4a6a5990b.jpg)
SGD优化器,450个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第38张图片](http://img.e-com-net.com/image/info8/52daeb4b309b4513bf2e94f5f6c641cc.jpg)
SGD优化器,500个epoch,学习率lr=0.25
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第39张图片](http://img.e-com-net.com/image/info8/5871814579c0460d951b64c53a96b0ad.jpg)
- 特别指出这个例子的原因是我发现epoch增大越到后期,生成出来的向日葵就基本都是
怼脸向日葵居多,而前面还能看到的苗条向日葵,则其实基本偏少了,更不用说其他更有特性的向日葵了。- 当我返回去看这
256张向日葵的数据集的时候,我发现其实原始的相册中,其实居多的也主要是怼脸向日葵,其次是苗条向日葵,最后是一些零散的各类较有个性的向日葵。- 尤次可见,最后的最后,我们导向的结果依然是
最后影响一个模型的质量的,还是回到了训练这个模型的数据集的质量。高质量的数据处理对模型的训练是非常非常非常重要的!
- 数据集照片情况概览:
4. 目前比较不错的效果展示
- 以下是使用
SGD优化器,学习率为0.25,训练了500个epoch的一个演变效果。
5. 一些其它问题和小小的总结
- 总得来说经过本次实验的探究,其实我所在对抗的主要是两个问题:
- "生成的图片不像我的目的图像"的问题。(欠拟合,未收敛)
- ”生成的图片大多长得类似,或者甚至一模一样!“(过拟合,模式崩塌)
- 结合做了以上那么多的实验来看,我现在对GAN网络的两个模型的损失函数的理解是正常的情况G和D应该是两条有波动,但整体上是对峙者推进的一上一下的趋势,其中最好是G在下,而D在上。这样的状态持续得越多个epoch,最终我们得到的生成器的综合效果就会越佳,而一旦打破了这个
平衡,生成器的质量就会往某一个方向偏移,一般是模式崩塌即判别器不断在进化,使得判别器太强,而生成器只能通过投机取巧的方式来精学某一类来保持它能继续保持能骗过生成器。所以如何达到平衡是一个值得深入研究的方向。
参考资料
- [1] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative Adversarial Nets[J/OL]. Journal of Japan Society for Fuzzy Theory and Intelligent Informatics, 2017: 177-177. http://dx.doi.org/10.3156/jsoft.29.5_177_2. DOI:10.3156/jsoft.29.5_177_2.
- GAN图像生成-mindspore
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第1张图片](http://img.e-com-net.com/image/info8/bcf2bcc857584002a9a425bf2236c2d5.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第2张图片](http://img.e-com-net.com/image/info8/e88b9f5ae31b4be6b7580ab8840886bc.jpg)
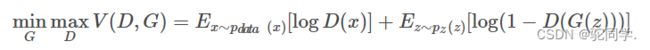
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第3张图片](http://img.e-com-net.com/image/info8/124bf99aeaa24b3aafede710f737d800.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第4张图片](http://img.e-com-net.com/image/info8/1bbf9dcc96b0488fbee6023de0acd937.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第5张图片](http://img.e-com-net.com/image/info8/598868f407034945a4d2bf1e916bc0d5.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第6张图片](http://img.e-com-net.com/image/info8/61153ef4ffdc4c96a432e0c83cd065e9.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第7张图片](http://img.e-com-net.com/image/info8/be4c16fc282f4c86a71149f6b58e048e.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第8张图片](http://img.e-com-net.com/image/info8/e695a552c60b46cf9615266114a6b26c.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第9张图片](http://img.e-com-net.com/image/info8/a85874845cc047f89e365ad86c166049.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第10张图片](http://img.e-com-net.com/image/info8/b55ba8d814e2481982ec5c86a42f03d2.gif)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第11张图片](http://img.e-com-net.com/image/info8/32f80facfaa4478e8ab9d7f0b382b703.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第12张图片](http://img.e-com-net.com/image/info8/b51ddd98c10a42dd85a67351867cf793.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第13张图片](http://img.e-com-net.com/image/info8/534555c20bc34624a485d95a3fef13ef.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第14张图片](http://img.e-com-net.com/image/info8/9c057ac4c57844d5a605ea91d15a9311.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第15张图片](http://img.e-com-net.com/image/info8/b27fac39edf14345a4bcc2deb30cf152.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第16张图片](http://img.e-com-net.com/image/info8/c2c7a3f532d64badba525774781440ab.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第17张图片](http://img.e-com-net.com/image/info8/f0c3a2eb10fa402cb3d4a1c97d5d6ef8.gif)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第18张图片](http://img.e-com-net.com/image/info8/171909d8f0644ffe8267506e1b466597.gif)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第19张图片](http://img.e-com-net.com/image/info8/8742d2743d0a40bbbc5c086b4f228b01.gif)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第20张图片](http://img.e-com-net.com/image/info8/591268ce479647db8ef92b3ea398b1ee.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第21张图片](http://img.e-com-net.com/image/info8/bd2ce560070b4d07880cf64848ed15b3.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第22张图片](http://img.e-com-net.com/image/info8/2050a611cbe846c79d3e0eea8c91faf3.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第23张图片](http://img.e-com-net.com/image/info8/f2e1242785424e50bd740540abc4a113.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第24张图片](http://img.e-com-net.com/image/info8/44e56259f2584ad181b247a9515d7062.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第25张图片](http://img.e-com-net.com/image/info8/b5fb3ca485e945f6b1be373002aae1f1.jpg)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第26张图片](http://img.e-com-net.com/image/info8/484ee499353e4a64bc5ef018b0afb7df.gif)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第27张图片](http://img.e-com-net.com/image/info8/a4320c48961742e58bd23cc72f5b8501.gif)
![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片_第28张图片](http://img.e-com-net.com/image/info8/be830c14ec3542d1ad1bac77d94e3d35.gif)