数据结构：选择排序

简单选择排序

选择排序是一种简单直观的排序算法。首先在未排序序列中找到最大（最小）的元素，存放到排序学列的其实位置，然后在剩余的未排序的元素中寻找最小（最大）元素，存放在已排序序列的后面

算法步骤

1. 在未排序序列中找到最大（小）元素，存放在排序序列的起始位置
2. 再从剩余的未排序序列中找到最大（小）元素，然后存放在已排序序列的后面
3. 重复上诉第二步骤，直至排序结束

算法理解

例如对无序表{56，12，80，91，20}采用简单选择排序算法进行排序，具体过程为：

• 第一次遍历时，从下标为 1 的位置即 56 开始，找出关键字值最小的记录 12，同下标为 0 的关键字 56 交换位置：

  

• 第二次遍历时，从下标为 2 的位置即 56 开始，找出最小值 20，同下标为 2 的关键字 56 互换位置：

  

• 第三次遍历时，从下标为 3 的位置即 80 开始，找出最小值 56，同下标为 3 的关键字 80 互换位置：

  

• 第四次遍历时，从下标为 4 的位置即 91 开始，找出最小是 80，同下标为 4 的关键字 91 互换位置：

  

• 到此简单选择排序算法完成，无序表变为有序表。

代码实现

#include "iostream"
using namespace std;

#define MAX 9
//单个记录的结构体
typedef struct {
    int key;
}SqNote;
//记录表的结构体
typedef struct {
    SqNote r[MAX];
    int length;
}SqList;
//交换两个记录的位置
void swap(SqNote *a,SqNote *b){
    int key=a->key;
    a->key=b->key;
    b->key=key;
}
//查找表中关键字的最小值
int SelectMinKey(SqList *L,int i){
    int min=i;
    //从下标为 i+1 开始，一直遍历至最后一个关键字，找到最小值所在的位置
    while (i+1<L->length) {
        if (L->r[min].key>L->r[i+1].key) {
            min=i+1;
        }
        i++;
    }
    return min;
}
//简单选择排序算法实现函数
void SelectSort(SqList * L){
    for (int i=0; i<L->length; i++) {
        //查找第 i 的位置所要放置的最小值的位置
        int j=SelectMinKey(L,i);
        //如果 j 和 i 不相等，说明最小值不在下标为 i 的位置，需要交换
        if (i!=j) {
            swap(&(L->r[i]),&(L->r[j]));
        }
    }
}
int main() {
    SqList *L = new SqList;
    L->length=8;
    L->r[0].key=49;
    L->r[1].key=38;
    L->r[2].key=65;
    L->r[3].key=97;
    L->r[4].key=76;
    L->r[5].key=13;
    L->r[6].key=27;
    L->r[7].key=49;
    SelectSort(L);
    for (int i=0; i<L->length; i++) {
        cout << L->r[i].key << " ";
    }
    return 0;
}

代码实现

13 27 38 49 49 65 76 97

树形选择排序

树形选择排序（又称“锦标赛排序”），是一种按照锦标赛的思想进行选择排序的方法，即所有记录采取两两分组，筛选出较小（较大）的值；然后从筛选出的较小（较大）值中再两两分组选出更小（更大）值，依次类推，直到最后选出一个最小（最大）值。同样可以采用此方式筛选出次小（次大）值等

算法理解

整个排序的过程，可以用一棵具有 n 个叶子结点的完全二叉树表示。例如对无序表{49，38，65，97，76，13，27，49}采用树形选择的方式排序，过程如下：

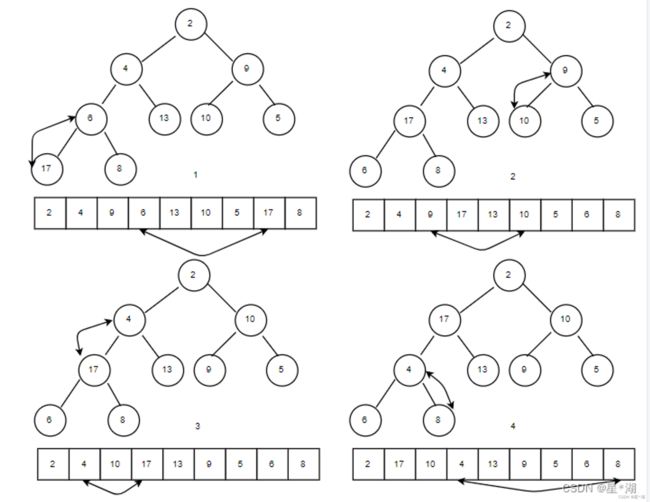
• 首先将无序表中的记录采用两两分组，筛选出各组中的较小值（如图 1 中的（a）过程）；然后将筛选出的较小值两两分组，筛选出更小的值，以此类推（如图 1 中的（b）（c）过程），最终整棵树的根结点中的关键字即为最小关键字：

图 1 树形选择排序（一）

• 筛选出关键字 13 之后，继续重复此方式找到剩余记录中的最小值，此时由于关键字 13 已经筛选完成，需要将关键字 13 改为“最大值”，继续重复此过程，如图 2 所示： 图 2 树形选择排序（二）

  

通过不断地重复此过程，可依次筛选出从小到大的所有关键字。该算法的时间复杂度为O(nlogn)，同简单选择排序相比，该算法减少了不同记录之间的比较次数，但是程序运行所需要的空间较多。

代码实现

#include "iostream"
using namespace std;
#define N 8
void TreeSelectionSort(int *mData)
{
    int MinValue = 0;
    int tree[N * 4]; // 树的大小
    int max, maxIndex, treeSize;
    int i, n = N, baseSize = 1;
    while (baseSize < n)
        baseSize *= 2;
    treeSize = baseSize * 2 - 1;
    for (i = 0; i < n; i++) {//将要排的数字填到树上
        tree[treeSize - i] = mData[i];
    }
    for (; i < baseSize; i++) {//其余的地方都填上最小值
        tree[treeSize - i] = MinValue;
    }
    // 构造一棵树，大的值向上构造
    for (i = treeSize; i > 1; i -= 2)
    {
        tree[i / 2] = (tree[i] > tree[i - 1] ? tree[i] : tree[i - 1]);
    }

    n -= 1;
    while (n != -1)
    {
        max = tree[1];        //树顶为最大值
        mData[n--] = max;     //从大到小倒着贴到原数组上
        maxIndex = treeSize;  //最大值下标
        while (tree[maxIndex] != max) {
            maxIndex--;
        }//找最大值下标
        tree[maxIndex] = MinValue;
        while (maxIndex > 1) {
            if (maxIndex % 2 == 0) {
                tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex + 1] ? tree[maxIndex] : tree[maxIndex + 1]);
            }
            else {
                tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex - 1] ? tree[maxIndex] : tree[maxIndex - 1]);
            }
            maxIndex /= 2;
        }
    }
}
int main()
{
    int a[N] = {49,38,65,97,76,13,27,49};
    TreeSelectionSort(a);
    for (int i = 0; i < N; i++) {
        cout << a[i] << " ";
    }
    return 0;
}

运行结果

13 27 38 49 49 65 76 97

堆排序

堆排序$(Heapsort)$是指利用堆来实现的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。堆排序的平均时间复杂度为 $O(nlogn)$。分为两种方法：

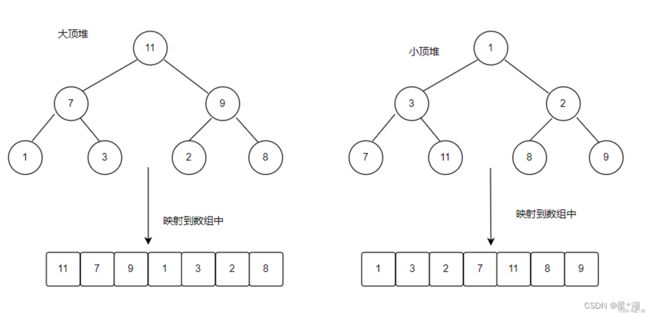
1. 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
2. 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

算法思想

了解了堆的基本性质之后，我们就可以看堆排序的基本思想。

1. 将未排序的序列构造成大（或者小）顶堆，根据堆的性质我们可以找到序列中的最大（或者最小）值
2. 把堆首和堆尾互换，并把堆的大小减$1$
3. 重复上面的步骤，直到堆的大小为$1$

代码实现

#include "iostream"
using namespace std;
#define MAX 9
//单个记录的结构体
typedef struct {
    int key;
}SqNote;
//记录表的结构体
typedef struct {
    SqNote r[MAX];
    int length;
}SqList;
//将以 r[s]为根结点的子树构成堆，堆中每个根结点的值都比其孩子结点的值大
void HeapAdjust(SqList * H,int s,int m){
    SqNote rc=H->r[s];//先对操作位置上的结点数据进行保存，放置后序移动元素丢失。
    //对于第 s 个结点，筛选一直到叶子结点结束
    for (int j=2*s; j<=m; j*=2) {
        //找到值最大的孩子结点
        if (j+1<m && (H->r[j].key<H->r[j+1].key)) {
            j++;
        }
        //如果当前结点比最大的孩子结点的值还大，则不需要对此结点进行筛选，直接略过
        if (!(rc.key<H->r[j].key)) {
            break;
        }
        //如果当前结点的值比孩子结点中最大的值小，则将最大的值移至该结点，由于 rc 记录着该结点的值，所以该结点的值不会丢失
        H->r[s]=H->r[j];
        s=j;//s相当于指针的作用，指向其孩子结点，继续进行筛选
    }
    H->r[s]=rc;//最终需将rc的值添加到正确的位置
}
//交换两个记录的位置
void swap(SqNote *a,SqNote *b){
    int key=a->key;
    a->key=b->key;
    b->key=key;
}
void HeapSort(SqList *H){
    //构建堆的过程
    for (int i=H->length/2; i>0; i--) {
        //对于有孩子结点的根结点进行筛选
        HeapAdjust(H, i, H->length);
    }
    //通过不断地筛选出最大值，同时不断地进行筛选剩余元素
    for (int i=H->length; i>1; i--) {
        //交换过程，即为将选出的最大值进行保存大表的最后，同时用最后位置上的元素进行替换，为下一次筛选做准备
        swap(&(H->r[1]), &(H->r[i]));
        //进行筛选次最大值的工作
        HeapAdjust(H, 1, i-1);
    }
}

int main() {
    SqList *L = new SqList ;
    L->length=8;
    L->r[1].key=49;
    L->r[2].key=38;
    L->r[3].key=65;
    L->r[4].key=97;
    L->r[5].key=76;
    L->r[6].key=13;
    L->r[7].key=27;
    L->r[8].key=49;
    HeapSort(L);
    for (int i=1; i<=L->length; i++) {
        cout << L->r[i].key << " ";
    }
    return 0;
}

运行结果

13 27 38 49 49 65 76 97

注意：堆排序相对于树形选择排序，其只需要一个用于记录交换（rc）的辅助存储空间，比树形选择排序的运行空间更小。