单张非二值mnist三分类实验数据汇总
在前述的实验中用mnist训练集0,1,2,3,4的第一张图片完成了10组三分类网络,并统计迭代次数和移位距离之间的关系。用间隔取点的办法实验了3*3,5*5,7*7,9*9,11*11,13*13,15*15共7个不同的尺寸。得到的数据如下
第一组
| 3*3 |
1*3*4 |
1*2*4 |
1*2*3 |
2*3*4 |
0*1*4 |
0*1*3 |
0*3*4 |
0*1*2 |
0*2*4 |
0*2*3 |
| δ |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
| 0.01 |
25528.5 |
24336.1 |
9492.618 |
9227.121 |
24070.39 |
7252.588 |
7084.342 |
6585.166 |
6482.06 |
5495.915 |
| 0.001 |
63278.92 |
59472.81 |
53485.31 |
52938.41 |
57616.89 |
45735.4 |
44602.2 |
42904.66 |
41677.61 |
31104.11 |
| 9.00E-04 |
66122.75 |
62414.27 |
58448.47 |
57679.9 |
60375.16 |
50398.23 |
48962.69 |
46693.44 |
45485.53 |
33925.72 |
| 8.00E-04 |
71480.41 |
67170.33 |
64717.14 |
63989.7 |
65406.67 |
55616.3 |
54172.61 |
52060.98 |
50660.67 |
37589.39 |
| 7.00E-04 |
77998.76 |
73028.56 |
72108.61 |
71477.29 |
70612.89 |
62793.99 |
61263.37 |
58467.27 |
57023.22 |
41898.17 |
| s3*3 |
3.498039 |
5.811765 |
5.701961 |
5.537255 |
4.14902 |
5.858824 |
5.827451 |
7.035294 |
7.082353 |
5.756863 |
将收敛误差为7e-4的迭代次数和移位距离s画成图
尽管s曲线的梯度不够丰富,但s也明显是一条增函数,用反比来解释s和n之间的关系也是合理的。
第二组
| 5*5 |
1*3*4 |
1*2*4 |
1*2*3 |
2*3*4 |
0*1*2 |
0*2*3 |
0*1*3 |
0*1*4 |
0*2*4 |
0*3*4 |
| δ |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
| 0.01 |
4852.327 |
3971.497 |
3849.93 |
3761.673 |
3297.035 |
3195.578 |
3172.513 |
3154.935 |
3044.357 |
2946.322 |
| 0.001 |
29105.61 |
23912.9 |
23347.73 |
22709.72 |
21140.85 |
20470.52 |
19926.4 |
19718.28 |
19372.02 |
18622.47 |
| 9.00E-04 |
31721.76 |
25924.04 |
25584.63 |
24772.43 |
23191.94 |
22528.86 |
21914.49 |
21523.96 |
21264.79 |
20455.74 |
| 8.00E-04 |
35248.12 |
28807.72 |
28230.64 |
27538.16 |
25774.16 |
24994.17 |
24202.72 |
23810.64 |
23577.19 |
22594.5 |
| 7.00E-04 |
39688.76 |
32526.52 |
31809.25 |
30926.7 |
29016.18 |
28110.4 |
27321.52 |
26921.52 |
26500.23 |
25583.64 |
| s5*5 |
9.992157 |
13.10588 |
12.83137 |
14.68235 |
19.04314 |
21.88235 |
18.36863 |
20.65098 |
22.92549 |
22.37647 |
由于尺寸的扩大弱化的对称性的影响,5*5的s曲线要平滑的多,明显n减小而s增加。
第三组
| 7*7 |
1*3*4 |
0*1*3 |
0*1*2 |
1*2*4 |
0*1*4 |
1*2*3 |
0*3*4 |
0*2*4 |
2*3*4 |
0*2*3 |
| δ |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
| 0.01 |
3322.899 |
3167 |
3143.392 |
3105.899 |
3064.558 |
2958.648 |
2899.251 |
2870.181 |
2811.055 |
2757.563 |
| 0.001 |
21089.87 |
20283.14 |
20079.41 |
19915.55 |
19733.9 |
19119.55 |
18779.49 |
18628.15 |
18248.59 |
18011.09 |
| 9.00E-04 |
23155.05 |
22309.77 |
22055.96 |
21966.31 |
21729.91 |
21002.09 |
20456.96 |
20371.83 |
20007.48 |
19863.38 |
| 8.00E-04 |
25824.88 |
24869.8 |
24543.71 |
24286.14 |
24056.1 |
23313.12 |
22740.74 |
22703.25 |
22255.98 |
21861.84 |
| 7.00E-04 |
28991.13 |
27854.08 |
27523.62 |
27278.07 |
26959.44 |
26239.79 |
25628.94 |
25490.19 |
24990.54 |
24667.68 |
| s7*7 |
22.2902 |
26.94902 |
29.81961 |
24.15686 |
25.78824 |
30.35294 |
29.78039 |
30.43137 |
30.72941 |
34.87843 |
n减小而s是增加的。
第四组
| 9*9 |
1*3*4 |
1*2*3 |
1*2*4 |
2*3*4 |
0*1*2 |
0*1*3 |
0*2*3 |
0*2*4 |
0*1*4 |
0*3*4 |
| δ |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
| 0.01 |
2675.106 |
2539.864 |
2526.673 |
2513.533 |
2521.915 |
2421.905 |
2397.648 |
2400.538 |
2330.372 |
2329.07 |
| 0.001 |
17858.37 |
16999.56 |
17071.4 |
16846.06 |
16699.34 |
16548.66 |
16261.65 |
16182.34 |
15971.54 |
15970.8 |
| 9.00E-04 |
19700.4 |
18658.47 |
18738.02 |
18506.6 |
18353.31 |
18201.87 |
17895.76 |
17746.46 |
17501.54 |
17508.73 |
| 8.00E-04 |
21862.45 |
20760.96 |
20900.6 |
20576.08 |
20509.6 |
20217.84 |
19941.41 |
19803.96 |
19503.26 |
19452.48 |
| 7.00E-04 |
24688.67 |
23522.75 |
23429.41 |
23133.07 |
23022.54 |
22821.45 |
22387.06 |
22187.65 |
22107.34 |
21977.67 |
| s9*9 |
36.1098 |
49.62353 |
41.16863 |
50.14118 |
52.1098 |
51.74902 |
57.21569 |
55.12941 |
47.10588 |
54.54118 |
n减小而s增加
第五组
| 11*11 |
0*1*4 |
0*1*3 |
1*2*3 |
1*3*4 |
0*1*2 |
2*3*4 |
1*2*4 |
0*2*3 |
0*3*4 |
0*2*4 |
| δ |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
| 0.01 |
2086.653 |
2105.02 |
2074.915 |
2124.95 |
2100.759 |
2036.005 |
2078.678 |
2017.995 |
1980.116 |
1999.779 |
| 0.001 |
14678.66 |
14780.6 |
14729.6 |
14709.63 |
14644.57 |
14515.06 |
14590.64 |
14355.45 |
14263.75 |
14187.57 |
| 9.00E-04 |
16236.9 |
16261.57 |
16201.7 |
16185.53 |
16027.33 |
15975.58 |
15987.5 |
15806.29 |
15611.98 |
15686.13 |
| 8.00E-04 |
18089.83 |
18132.21 |
17968.03 |
17963.97 |
17926.63 |
17792.76 |
17879.34 |
17631.35 |
17401.24 |
17441.43 |
| 7.00E-04 |
20504.19 |
20469.01 |
20376.85 |
20359.39 |
20180.85 |
20158.58 |
20156.69 |
19930.71 |
19702.99 |
19689.2 |
| s11*11 |
90.24314 |
87.59216 |
89.87451 |
74.32157 |
93.19216 |
89.82745 |
88.96471 |
100.6431 |
93.36471 |
97.64706 |
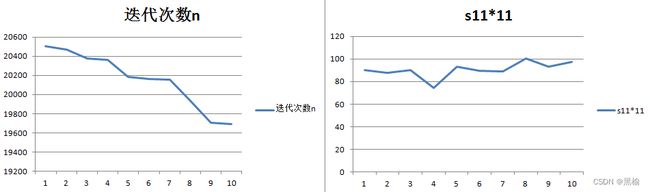
同样可以观察到n和s之间的反比关系
第六组
| 13*13 |
1*3*4 |
1*2*4 |
0*1*4 |
0*1*3 |
0*1*2 |
1*2*3 |
2*3*4 |
0*3*4 |
0*2*4 |
0*2*3 |
| δ |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
| 0.01 |
2006.427 |
1984.819 |
1947.497 |
1938.794 |
1939.975 |
1923.412 |
1911.729 |
1849.111 |
1877.201 |
1848.739 |
| 0.001 |
14151.85 |
14124.55 |
14116.28 |
13974.28 |
13992.44 |
13923.85 |
13857.63 |
13582.78 |
13632.16 |
13553.69 |
| 9.00E-04 |
15633.13 |
15540.86 |
15572.98 |
15450.58 |
15336.95 |
15375.03 |
15288.71 |
14917.5 |
14986.11 |
14884.89 |
| 8.00E-04 |
17463.22 |
17301.26 |
17309.79 |
17209.39 |
17054.93 |
17063.92 |
16990.42 |
16651.06 |
16760.05 |
16691.82 |
| 7.00E-04 |
19748.09 |
19635.53 |
19609.79 |
19470.3 |
19427.75 |
19392.49 |
19240.36 |
18987.97 |
18964.32 |
18876.56 |
| s13*13 |
94.28235 |
104.7922 |
113.8824 |
117.3804 |
120.651 |
116.4706 |
115.0039 |
123.4196 |
123.8118 |
133.8824 |
13*13的s曲线非常平滑,n与s的反比关系非常明显
第七组
| 15*15 |
1*2*3 |
0*1*2 |
0*2*3 |
0*2*4 |
1*2*4 |
2*3*4 |
0*1*4 |
0*3*4 |
0*1*3 |
1*3*4 |
| δ |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
迭代次数n |
| 0.01 |
2100.879 |
2020.663 |
1988.266 |
1990.347 |
1959.749 |
1964.513 |
1806.965 |
1803.508 |
1778.141 |
1757.03 |
| 0.001 |
14604.79 |
14516.06 |
14299.3 |
14332.46 |
14182.17 |
14162.15 |
13370.29 |
13356.84 |
13191.83 |
13021.52 |
| 9.00E-04 |
16163.44 |
15959.09 |
15860.1 |
15730.95 |
15650.05 |
15603.02 |
14687.98 |
14662.88 |
14608.69 |
14392.83 |
| 8.00E-04 |
17967.66 |
17817.04 |
17683.23 |
17555.33 |
17424.39 |
17368.5 |
16346.61 |
16352.7 |
16272.56 |
16024.08 |
| 7.00E-04 |
20210.69 |
20140.15 |
19915.37 |
19795.33 |
19791.92 |
19717.7 |
18671.6 |
18648.29 |
18348.53 |
18162.27 |
| s |
105.4118 |
115.9216 |
128.5569 |
119.1686 |
111.9137 |
117.3569 |
144.0392 |
149.4039 |
140.698 |
130 |
同样可以观察到n和s的反比关系。
因此这7组数据,尽管有的s曲线不够平滑,但用n和s之间的反比关系来理解这7组数据都是直观而实用的。
| 0*1*2 |
0*1*3 |
0*1*4 |
0*2*3 |
0*2*4 |
0*3*4 |
1*2*3 |
1*2*4 |
1*3*4 |
2*3*4 |
|
| s3*3 |
7.035294 |
5.858824 |
4.14902 |
5.7568627 |
7.0823529 |
5.827451 |
5.7019608 |
5.8117647 |
3.4980392 |
5.5372549 |
| s5*5 |
19.04314 |
18.36863 |
20.65098 |
21.882353 |
22.92549 |
22.376471 |
12.831373 |
13.105882 |
9.9921569 |
14.682353 |
| s7*7 |
29.81961 |
26.94902 |
25.78824 |
34.878431 |
30.431373 |
29.780392 |
30.352941 |
24.156863 |
22.290196 |
30.729412 |
| s9*9 |
52.1098 |
51.74902 |
47.10588 |
57.215686 |
55.129412 |
54.541176 |
49.623529 |
41.168627 |
36.109804 |
50.141176 |
| s11*11 |
93.19216 |
87.59216 |
90.24314 |
100.64314 |
97.647059 |
93.364706 |
89.87451 |
88.964706 |
74.321569 |
89.827451 |
| s13*13 |
120.651 |
117.3804 |
113.8824 |
133.88235 |
123.81176 |
123.41961 |
116.47059 |
104.79216 |
94.282353 |
115.00392 |
| s15*15 |
115.9216 |
140.698 |
144.0392 |
128.55686 |
119.16863 |
149.40392 |
105.41176 |
111.91373 |
130 |
117.35686 |
比较移位距离的变化
移位距离s的变化非常规则,随着尺寸的增加而增加
再比较各个尺寸的迭代次数的大小顺序
| 3*3 |
1*3*4 |
1*2*4 |
1*2*3 |
2*3*4 |
0*1*4 |
0*1*3 |
0*3*4 |
0*1*2 |
0*2*4 |
0*2*3 |
| 5*5 |
1*3*4 |
1*2*4 |
1*2*3 |
2*3*4 |
0*1*2 |
0*2*3 |
0*1*3 |
0*1*4 |
0*2*4 |
0*3*4 |
| 7*7 |
1*3*4 |
0*1*3 |
0*1*2 |
1*2*4 |
0*1*4 |
1*2*3 |
0*3*4 |
0*2*4 |
2*3*4 |
0*2*3 |
| 9*9 |
1*3*4 |
1*2*3 |
1*2*4 |
2*3*4 |
0*1*2 |
0*1*3 |
0*2*3 |
0*2*4 |
0*1*4 |
0*3*4 |
| 11*11 |
0*1*4 |
0*1*3 |
1*2*3 |
1*3*4 |
0*1*2 |
2*3*4 |
1*2*4 |
0*2*3 |
0*3*4 |
0*2*4 |
| 13*13 |
1*3*4 |
1*2*4 |
0*1*4 |
0*1*3 |
0*1*2 |
1*2*3 |
2*3*4 |
0*3*4 |
0*2*4 |
0*2*3 |
| 15*15 |
1*2*3 |
0*1*2 |
0*2*3 |
0*2*4 |
1*2*4 |
2*3*4 |
0*1*4 |
0*3*4 |
0*1*3 |
1*3*4 |
如果n和s之间的反比关系是严格的,n的顺序也应该是一致的,但有少部分数据分布比较分散如0*1*4,或许是由于对于单张图片对称性导致的结构耦合效应弱化了n和s之间的线性关系。
比较迭代次数的变化
| 0*1*2 |
0*1*3 |
0*1*4 |
0*2*3 |
0*2*4 |
0*3*4 |
1*2*3 |
1*2*4 |
1*3*4 |
2*3*4 |
||
| 3*3 |
7.00E-04 |
58467.27 |
62793.99 |
70612.89 |
41898.171 |
57023.216 |
61263.367 |
72108.608 |
73028.558 |
77998.759 |
71477.286 |
| 5*5 |
7.00E-04 |
29016.18 |
27321.52 |
26921.52 |
28110.397 |
26500.226 |
25583.643 |
31809.251 |
32526.523 |
39688.764 |
30926.698 |
| 7*7 |
7.00E-04 |
27523.62 |
27854.08 |
26959.44 |
24667.683 |
25490.191 |
25628.94 |
26239.789 |
27278.07 |
28991.131 |
24990.543 |
| 9*9 |
7.00E-04 |
23022.54 |
22821.45 |
22107.34 |
22387.06 |
22187.648 |
21977.673 |
23522.754 |
23429.407 |
24688.673 |
23133.065 |
| 11*11 |
7.00E-04 |
20180.85 |
20469.01 |
20504.19 |
19930.709 |
19689.196 |
19702.99 |
20376.849 |
20156.688 |
20359.392 |
20158.583 |
| 13*13 |
7.00E-04 |
19427.75 |
19470.3 |
19609.79 |
18876.558 |
18964.322 |
18987.97 |
19392.492 |
19635.528 |
19748.085 |
19240.362 |
| 15*15 |
7.00E-04 |
20140.15 |
18348.53 |
18671.6 |
19915.367 |
19795.327 |
18648.286 |
20210.688 |
19791.925 |
18162.266 |
19717.704 |
图片尺寸扩大,迭代次数是减小的。把所有的迭代次数和移位距离画到一起
3*3 用神经网络模拟3个距离为0的粒子
5*5 将神经网络粒子化的内在合理性
7*7 近似对称性对迭代次数的影响
9*9 决定迭代次数的两种效应
11*11 验算迭代次数和移位距离之间的反比关系
13*13用移位距离去比较迭代次数的大小
15*15关于迭代次数的一个反比关系