在很多任务中都用得到滑动窗口,比如密集人群计数,标签文件是一张与图片尺寸等大的二维矩阵,人头的中心位置为1,其他位置为0。我想求出这张图片中人头最稠密的一块区域(区域尺寸给定),那么怎么求呢?
我想到的办法就是用这个区域的尺寸作为一个固定窗口,在整个标签矩阵中滑动,每滑动到一处,就计算一下当前窗口中 “1” 的个数,数量最多(加和最大)的区域就是人头最稠密的区域,即当前的窗口。对于滑动窗口计算,最容易想到的就是用两层for循环来实现,但首先它需要处理边界的问题,其次随着图片的尺寸的增大,效率会变地很低,内存占用也非常大。
本文使用numpy来完成滑窗计算,并计算元素值相加的和最大的一块区域(区域的尺寸设定为卷积核的尺寸)。为了增加算法的普遍性,标签文件中元素的值不局限于0,1两个数字,为了解决这个变动带来的问题,需要在窗口滑动计算后增加一个小块区域内元素相加的动作,顺着这个思路可以额外完成使用numpy实现最大和均值两种池化的任务。
拿一个最简单的例子来完成下文的讨论:
$$ X= \left[ \begin{matrix} 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] $$
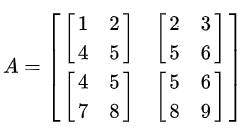
如果kernal的大小是2x2,stride为1,那么滑窗计算的结果就是下面的4个小矩阵组成的新矩阵A:
到这里,手工计算版的滑动窗口就结束了。后续任务,4个小矩阵各自求和,得到[12,16,24,28]四个值,可知元素值相加的和最大的一块区域是最右下角的那一块。
下面用程序来复现上面的讨论。
def pool2d(X, kernel_size, stride, padding, pool_mode='avg'):
# 第一步
X = np.pad(X, padding, mode='constant')
# 第二步
output_shape = ((X.shape[0] - kernel_size[0] + 2*padding)//stride + 1, (X.shape[1] - kernel_size[1] + 2*padding)//stride + 1)
# 第三步
A = as_strided(X, shape = output_shape + kernel_size, strides = (stride*X.strides[0], stride*X.strides[1]) + X.strides)
# 第四步
A = A.reshape(-1, *kernel_size) # 把四维压缩到三维
# 第五步
if pool_mode == 'max':
return A, A.max(axis=(1,2)).reshape(output_shape) # 实现最大池化任务
elif pool_mode == 'avg':
return A, A.mean(axis=(1,2)).reshape(output_shape) # 实现均值池化任务
第一步:边缘填充
对矩阵进行池化操作,参数constant表示连续填充相同的值,即padding。一般是全零填充。
第二步:尺寸预计算
预先计算窗口滑动后每个小矩阵Ai的尺寸,这部分就可以根据卷积前后尺寸的变化公式来计算:
new=(old-kennel_size+2*padding)/stride+1在上面的例子中output_shape就是(2,2)。 【 (4-2+2*0)//2+1=2】
第三步:滑窗计算
调用as_strided 函数进行窗口滑动计算。该函数主要的参数有三个:
- 要操作的矩阵,不用多说了。
- shape:返回矩阵的尺寸,区别于之前的“output_shape”,这个shape是指矩阵A的尺寸,即所有小矩阵放在一块的尺寸,这个尺寸不一定等于输入矩阵X的尺寸。比如上面的例子,shape就是
(2,2,2,2),而输入矩阵X的尺寸是(3,3)。 strides:这是numpy数组的一个属性,官方手册给出的解释是跨越数组各个维度所需要经过的字节数(bytes)。用上面的矩阵X当例子说明:
- 从
X[0][0]到X[0][1]需要经过4个字节,为什么是4个?因为a的数据类型是int32,正好占4个字节. 从
X[0][0]到X[1][0]需要经过12个字节,为什么是12个?因为python是行顺序优先的编程语言,即读取矩阵元素时是一行一行来读的,把矩阵X展平,就是[0 1 2 3 4 5 6 7 8],从0到3就需要遍历3个元素,而每个元素都是4个字节,所以总共需要12个字节。注1:常见的编程语言中,只有matlab和fortran是列顺序优先。
注2:想要更深入地了解strides,推荐文章【卷积算法另一种高效实现,as_strided详解】
- 从
这一步返回的结果就是下面的矩阵A,尺寸为(2,2,2,2) 。
第四步:稠密区域搜寻任务
其实滑动窗口计算到第三步就已经结束了,这一步就是重新调整一下尺寸,将(2,2,2,2)调整成(4,2,2),即第一维变成小矩阵的个数,后面两维是小矩阵的尺寸。对每个小矩阵加和再比较就能知道加和最大的一块区域了,继而完成稠密区域搜寻任务。
第五步:两类池化任务
以平均池化为例,调用如下函数
A.mean(axis=(1,2)).reshape(output_shape)axis=(1,2)是因为此时的矩阵A维度为(4,2,2),要从第二个维度开始处理。
reshape(output_shape)是因为按照池化任务的要求,输出结果要与小矩阵的维度一致,即(2,2)。
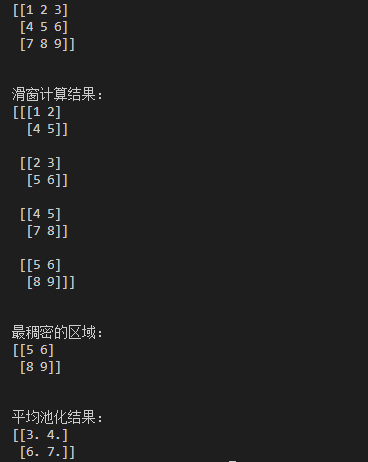
程序运行结果:
参考:https://zhuanlan.zhihu.com/p/64933417