链式二叉树的简单实现(C语言数据结构)

链式二叉树的简单实现(C语言数据结构)

1.前言

本篇谈论一下二叉树(BinaryTree)的简单实现。实际上，二叉树的实现不止有链式结构，顺序表数组也可以实现。不过当人们谈到二叉树，第一时间可能肯定会想到链式结构，故笔者简单使用C语言实现其链式结构。

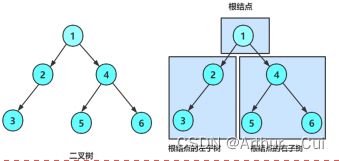
综合来讲，二叉树是：

1.空树

2.非空：由根节点、根节点左子树、根节点右子树共同组成的。

---

从概念可以看出，二叉树定义是递归式的，因此后续操作基本都是按照此概念实现的。

2.基本结构

笔者将所有代码实现分为三个文件：

1.BinaryTree.h头文件用来放头文件包含、结构体定义和函数声明。

2.BinaryTree.c文件用来置放各函数的具体实现。

3.Test.c用来包含主函数和测试二叉树的代码。

2.1结构体

#include
#include
#include

typedef int BTDataType;
typedef struct BinaryTreeNode    //链式二叉树
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

该结构体包含数据、左子树和右子树三个内容。

---

2.2函数声明

void PrevOrder(BTNode* root);   //前序遍历
void InOrder(BTNode* root);		//中序遍历
void PostOrder(BTNode* root);	//后序遍历

BTNode* BuyBTNode(BTDataType x); //创建内存
int TreeSize(BTNode* root);    //求所有节点个数
int TreeLeafSize(BTNode* root);//求叶子结点个数
int TreeHeight(BTNode* root); //树的深度
int TreeLevelSize(BTNode* root,int k); //求第k层的节点个数  k>=1
BTNode* TreeFind(BTNode* root, BTDataType x);   //查找值为x的节点
void TreeDestroy(BTNode* root);   // 销毁

当实现二叉树后尽量涵盖一个简单二叉树的所有功能包括：求节点个数，第k层个数，叶子结点个数，深度，查找等等功能。

---

3.具体函数实现

3.1二叉树的前中后序遍历等

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉

树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历

是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

void PrevOrder(BTNode* root)   //前序遍历
{
	if (root == NULL)
	{
		printf("NULL ");
		return;     //返回上一级
	}
	printf("%d ",root->data);  //根
	PrevOrder(root->left);		//左
	PrevOrder(root->right);		//右

}

2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

   void InOrder(BTNode* root)		//中序遍历
   {
   	if (root == NULL)
   	{
   		printf("NULL ");
   		return;     //返回上一级
   	}
   
   	
   	InOrder(root->left);    //左
   	printf("%d ",root->data);  //根
   	InOrder(root->right);	//右
   }
   

3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

   void PostOrder(BTNode* root)	//后序遍历
   {
   	if (root == NULL)
   	{
   		printf("NULL ");
   		return;     //返回上一级
   	}
   
   	
   	PostOrder(root->left);    //左
   	PostOrder(root->right);	//右
   	printf("%d ", root->data);  //根
   
   }
   

不难发现，以上三种遍历都使用到了递归实现。具体结构正如下图：

3.2二叉树节点个数等

求结点总个数****TreeSize()

int TreeSize(BTNode* root)
{
	return root == NULL ? 0 :
		TreeSize(root->left) + TreeSize(root->right)+1; //返回左右子树结点+自己（1）
}

求叶子结点个数TreeLeafSize()

int TreeLeafSize(BTNode* root)  //叶子结点
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL) //到了叶子结点就返回
	{
		return 1;
	}
	return TreeLeafSize(root->left) +
		TreeLeafSize(root->right);
}

求第k层的节点个数TreeLevelSize()

int TreeLevelSize(BTNode* root, int k) //求第k层的节点个数  k>=1
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeLevelSize(root->left, k - 1)
		+   TreeLevelSize(root->right, k - 1);
}

3.3树的深度和查找等

求树的深度***TreeHeight(BTNode root)

int TreeHeight(BTNode* root) //树的深度
{
	if (root == NULL)
	{
		return NULL;
	}
	int LeftHeight = TreeHeight(root->left);   //记下每次的值 防止多次调用浪费空间
	int RightHeight = TreeHeight(root->right);

	return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;

}

**这里值得注意的是：**一定要手动定义LeftHeight(右子树同理),而不能直接return root的左节点root->left，否则返回的时候值没有记录下来将会丢失！！

查找值函数

BTNode* TreeFind(BTNode* root, BTDataType x)    //查找
{
	if (root == NULL)
		return NULL;
	if (root->data == x) //找到则返回节点
		return root;
	BTNode* ret1 = TreeFind(root->left, x); //记录下左子树后不为空返回
	if (ret1)
		return ret1;
	BTNode* ret2 = TreeFind(root->right,x);//记录下右子树不为空返回
	if (ret2)
		return ret2;
	return NULL;  //否则返回空
}

3.4其余函数收尾等

**创建节点函数BuyBTNode()**函数

BTNode* BuyBTNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	node->data = x;
	node->left = node->right = NULL;
	return node;
}

注意：malloc创建内存后如果不判断为空 VS2019和VS2022可能会判错！！

函数销毁Destroy()

void TreeDestroy(BTNode* root)   // 销毁
{
	if (root == NULL)
		return;
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
}

注意：free释放内存的先后无所谓

4.主函数的测试

int main()
{

	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);
	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n4->left = n5;
	n4->right = n6;


	PostOrder(n1);  //后序遍历
	printf("\n");
	printf("TreeSize:%d\n",TreeSize(n1));
	printf("TreeLeafSize:%d\n",TreeLeafSize(n1));
	printf("TreeHeight:%d\n", TreeHeight(n1));
	printf("TreeLevelSize:%d\n",TreeLevelSize(n1,3));


	TreeDestroy(n1);
	n1 = NULL;
	return 0;
}

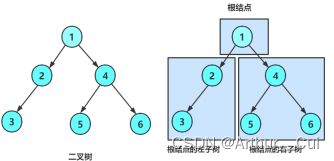
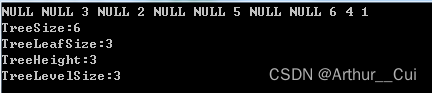
在主函数中手动连接造出如图一的简单二叉树并使用输出函数测试成功与否

来看看结果：

5.总结：

链式二叉树的实现离不开递归思想。在实现过程中有任何不明白的画张图便可知晓。

看到这里的老铁们如果觉得写的不错点点赞吧！