动态规划——背包问题整理(01背包+完全背包)
1、引言
背包问题简单描述,其实就是有一堆物品同时具有一定价值和重量,现有一个背包可以承受最大重量m,那么要怎么选择在不超过背包最大重量的前提下,使背包中选择的物品价值最大。
最常见的背包问题又可以分为:01背包和完全背包,图示如下:
(图片引自:代码随想录)
2、标准01背包分析
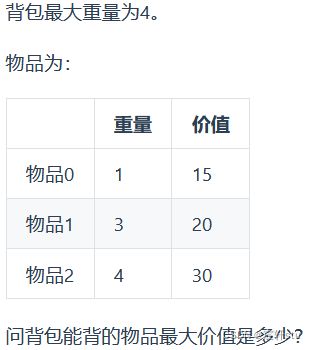
(1)问题描述
(2)分析
最直接的想法应该是暴力解法,每一件物品只存在两种状态,拿或者不拿,那么便可以采用回溯的思想例举出所有可能,然后找到价值最大的组合,但我们会发现时间复杂度就到了O(2^n),n代表物品的种类数。也就是采用暴力解法会带来指数级别的时间复杂度,因此,我们可以考虑采用动态规划来求解。
动态规划五步曲前四步:
1)确定dp含义
因为同时存在物品种类和背包最大重量,要求组合的最大价值。我们可以采用二维数组表示,即 dp[i][j],表示从物品0~i中任意取,放进容量为j的背包中,价值总和最大是多少。
2)递推公式
根据dp的定义,我们可以从两个方向来推导dp:
不取物品i:从dp[i-1][j]进行推导,即背包的容量为j,里面不放物品i的最大价值。此时的dp[i][j]就是dp[i-1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值。
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3)dp初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
其次是根据递推公式还需要初始化dp[0][j],当背包的容量j
此时dp数组初始化情况如图所示:
4)确定遍历顺序
根据上文的分析,我们可以发存在两个维度(物品 和背包重量),那么是先遍历背包 还是 物品呢?
根据递推公式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。也就是说当前状态是由表的左上方递推过来的,不管先遍历谁,都是可以的,具体要根据那种遍历方式更好理解来定。
a、先遍历物品,然后遍历背包重量:
// weight物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}b、先遍历背包 再遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}(3)、完整代码
public static void main(string[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
testweightbagproblem(weight, value, bagsize);
}
public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
int wlen = weight.length, value0 = 0;
//定义dp数组:dp[i][j]表示背包容量为j时,前i个物品能获得的最大价值
int[][] dp = new int[wlen + 1][bagsize + 1];
//初始化:背包容量为0时,能获得的价值都为0
for (int i = 0; i <= wlen; i++){
dp[i][0] = value0;
}
//初始化 只选择物品0时,背包重量变化dp[0][j]初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 1; i <= wlen; i++){
for (int j = 1; j <= bagsize; j++){
if (j < weight[i - 1]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
}
}
}
}(4)01背包问题之滚动数组实现,dp二维降一维
一维dp数组(滚动数组),其实就是对背包问题的状态压缩;
在使用二维数组来表示dp时,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
动规五部曲分析如下:
1)确定dp含义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2)递推公式
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,公式如下:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);3)初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
4)遍历顺序
我们这里采用先遍历物品再遍历背包容量的顺序,要时刻注意dp[j]表示的含义是当背包最大容量为j时选择物品能够得到的最大价值;
我们要注意 二维dp和现在压缩到一维dp在遍历顺序上不同,一维dp遍历顺序如下:
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量,注意背包容量倒序遍历
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}二维dp遍历顺序中背包容量是从小到大,一维dp遍历顺序背包容量是从大到小,一维dp背包容量倒序遍历的目的是保证物品i只被放入一次,若采用正序遍历会导致物品i被重复加入多次。
5) 代码
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWight = 4;
testWeightBagProblem(weight, value, bagWight);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
int len = weight.length;
//定义dp数组,dp[j]表示背包容量为j时,能够获得的最大价值
int[] dp = new int[bagweigth +1];
//遍历顺序: 先遍历物品,再遍历背包容量
for(int i=0;i=weigth[i];j--){
dp[j] = Math.max(dp[j], dp[j-weight[i]]+value[i]);
}
}
return dp[bagweight];
} ------------------------------------------------------------------------------------------------------------
3、完全背包问题
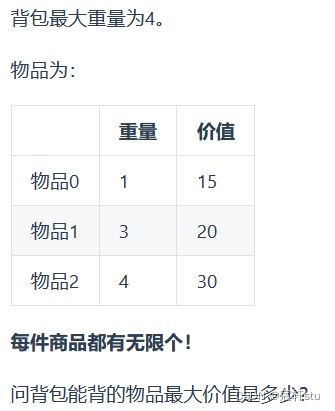
相对于01背包问题,每件物品只有一样,我们的选择是拿或者不拿;但对于完全背包问题,每件物品有无数个,同样求解将哪些物品放入背包中,可以使得背包放入物品的总价值最大:
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件;
案例如下:
我们需要特别注意到完全背包和01背包的区别:物品具有无数个;而我们在用一维dp求解01背包问题的时候,采用先遍历物品再遍历背包(其中背包遍历倒序)的顺序,目的是避免商品被无数次使用(见上文分析)。但此时,完全背包正需要的是无数次商品添加,所以我们可以采用一维dp的正序遍历来完成。
首先是01背包的一维dp:
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}其中,01背包一维dp 遍历背包采用倒序,目的是保证每件商品只选用了一次;
因为完全背包可以重复选择商品,故我们在一维dp基础上采用正序遍历,如下:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j < bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
ps:
1) 01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
2) 在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序同样无所谓!