3D空间中射线与轴向包围盒AABB的交叉检测算法
引言
在上一节中,我讲述了如何实现射线与三角形的交叉检测算法。但是,我们应该知道,在游戏开发中,一个模型有很多的三角形构成,如果要对所有的物体,所有的三角形进行这种检测,就算现在的计算机运算能力,也是无法高效的完成。所以,我们需要通过其他的手段来提早剔除一些不可能发生交叉的物体,这种早退的思想,大量的运用在3D游戏技术中。在本篇文章中,我将像大家讲述如何实现射线与轴向包围盒AABB的交叉检测。如果读者不明白什么是轴向包围盒,请看这篇文章。
Ray-AABB交叉检测算法
现如今,有很多的Ray-AABB交叉检测算法,这里主要讲述一种称之为"Slabs method"的交叉检测算法。
在3D空间中,我们先确定正对着射线的三个面,也就是说,我们可以通过某种方式将AABB相对于射线Ray的背面给忽略掉,从而确定三个候选的面。这三个候选的面,就是有可能和射线Ray发生交叉的最近的面。同时,我们还需要知道一个事实:当射线与这三个候选面中的一个发生交叉之后,射线Ray的原点到这个面的距离要比到其他几个面的距离要长。
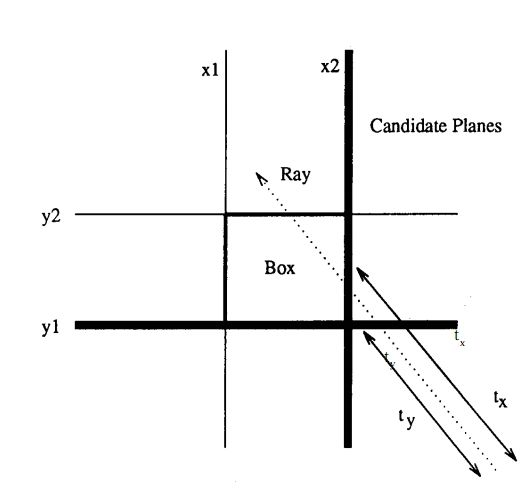
如果对于上面的事实不是很清楚的话,我们来看下图:
在上图中,我们的射线在右下角,向左上角发射。所以,候选面就是y1面,和x2面(这里由于讲述的方便,使用2D图形来表示)。ty是射线到y1面的距离,tx是射线到x2的距离。从上图中可以看出tx > ty, 而射线与x2平面相交叉。
通过上图,大家就应该明白了,上面那个事实的含义了。这个算法也就是基于此等事实来实现的。
我们知道射线的公式为R(t) = O + t * D,上图中所说的射线到某个面的距离,实际上就是射线原点到射线与该平面的交叉点的距离,而这个距离,刚好就是我们将平面方程带入R(t) = O + t * D中,计算出来的t的值。所以,我们现在要做的就是确定哪几个面试候选面,并且将候选面的方程带入到R(t) = O + t * D中,求出t的值,同时我们还要确保求出的交叉点在AABB盒上,才能够算作发生了交叉,如果仅仅是求出最大的t值,而不保证交点是否在AABB盒上,算法也是无效的。
在上面,讲述了算法的大概流程,但是,还有几个问题需要解决。
首先:
1.如何确定候选面
2.如何确定候选面的方程
3.如何对交叉点是否在AABB盒上进行判断
下面我们来依次解决这几个问题。
对于问题1,很简单,如上图中的y1平面和y2平面来说,只要将平面方程带入射线Ray的方程,求出这两个平面的t值,然后t值较小的那个自然先与射线交叉,那么就表示它是一个候选面了。可以看出,解决这个问题的方法还是要确定平面的方程。这个问题刚好是问题2。
我们可以使用如下的方程来表示某一个候选面的方程:
X * n = d ; 其中X表示的就是该候选面上的点,n表示的是该面的法线,注意一个面有两个法线,我们使用的法线并不是像3D图形学中某个顶点法线那样的定义,在这里,我们一致使用某个分量为1的法线,也就是说,如果上面的方程表示的是AABB盒的左面的面,那么公式中的n表示的就是(1,0,0),但上面的公式表示的是AABB盒的右边的面的时候,n表示的值依然是(1,0,0)。读者看到这里,可能要骂娘了,为毛这么搞,干嘛要搞一样的法线,为什么不像DirectX里面定义顶点法线那样来定义了?额,这样表示其实是一个编程技巧,当后面看代码的时候,就能够明白这样做的好处了。在明白了n怎么样表示之后,还剩下d。这里的d表示的就是这个AABB盒的这个面在垂直于该面的那个轴上的分量。也就是说,如果上面表示的是AABB盒的左边的面的时候,d表示的就是这个面上所有点的x坐标(由于是轴向包围盒AABB,所以左边的面的x坐标都是一样的)。注意,这里表示的是坐标值,也就是表示带有方向的。这样说,读者可能又不理解了,平面上的点和平面的法线点积怎么可能会是负值了。额,的确,如果使用的是DirectX中顶点的法线定义方式的时候,从原点到平面上的点所构成的向量与DirectX法线的点积肯定是一个正数,但是亲爱的读者啊,我这里使用的并不是那种法线定义方式,所以还请原谅,这里的d值有可能就是负值了。
好了,费了很大的力气讲解这个公式的来历,希望读者可以好好的明白下上面那些话的意义。通过上面的公式,我们就能够将这个公式带入到射线方程中,从而得到如下的结果:
t = (d - O * n) / (D * n) 。对于AABB盒来说,它的面的法线总是有两个分量是0,而另外一个分量由于我上面讲述的那种技巧,使得那个分量总是为1,所以就能够得到如下的统一的t值公式:
当候选面垂直与x轴的两个面时,t = (d - Ox) / Dx
当候选面垂直与y轴的两个面时,t = (d - Oy) / Dy
当候选面垂直与z轴的两个面时,t = (d - Oz) / Dz
有了方程之后,我们就可以求出t值了。
现在就剩下最后一个问题了,如何确保求出的t值所表示的那个交叉点是在AABB盒上的了??
为了求出这个问题,我们需要在求t值的过程中,保留另外三个并不是候选面t值。然后,通过这些t值来确定是否在AABB盒上。这个过程将在代码中展示出来,因为只是简单的比较操作,所以不再赘述。
Ray-AABB交叉算法实现
下面是我实现的一个版本的代码:
bool Ray::intersectWithAABB(AABB* a, VECTOR3* vcHit)
{
float tmin = 0.0f ;
float tmax = FLT_MAX ;
//The plane perpendicular to x-axie
if(abs(dir.x) < 0.000001f) //If the ray parallel to the plane
{
//If the ray is not within AABB box, then not intersecting
if(origin.x < a->min.x || origin.x > a->max.x)
return false ;
}
else
{
//Compute the distance of ray to the near plane and far plane
float ood = 1.0f / dir.x ;
float t1 = (a->min.x - origin.x) * ood ;
float t2 = (a->max.x - origin.x) * ood ;
//Make t1 be intersecting with the near plane, t2 with the far plane
if(t1 > t2)
{
float temp = t1 ;
t1 = t2 ;
t2 = temp ;
}
//Compute the intersection of slab intersection intervals
if(t1 > tmin) tmin = t1 ;
if(t2 < tmax) tmax = t2 ;
//Exit with no collision as soon as slab intersection becomes empty
if(tmin > tmax) return false ;
}// end for perpendicular to x-axie
//The plane perpendicular to y-axie
if(abs(dir.y) < 0.000001f) //If the ray parallel to the plane
{
//If the ray is not within AABB box, then not intersecting
if(origin.y < a->min.y || origin.y > a->max.y)
return false ;
}
else
{
//Compute the distance of ray to the near plane and far plane
float ood = 1.0f / dir.y ;
float t1 = (a->min.y - origin.y) * ood ;
float t2 = (a->max.y - origin.y) * ood ;
//Make t1 be intersecting with the near plane, t2 with the far plane
if(t1 > t2)
{
float temp = t1 ;
t1 = t2 ;
t2 = temp ;
}
//Compute the intersection of slab intersection intervals
if(t1 > tmin) tmin = t1 ;
if(t2 < tmax) tmax = t2 ;
//Exit with no collision as soon as slab intersection becomes empty
if(tmin > tmax) return false ;
}// end for perpendicular to y-axie
//The plane perpendicular to z-axie
if(abs(dir.z) < 0.000001f) //If the ray parallel to the plane
{
//If the ray is not within AABB box, then not intersecting
if(origin.z < a->min.z || origin.z > a->max.z)
return false ;
}
else
{
//Compute the distance of ray to the near plane and far plane
float ood = 1.0f / dir.z ;
float t1 = (a->min.z - origin.z) * ood ;
float t2 = (a->max.z - origin.z) * ood ;
//Make t1 be intersecting with the near plane, t2 with the far plane
if(t1 > t2)
{
float temp = t1 ;
t1 = t2 ;
t2 = temp ;
}
//Compute the intersection of slab intersection intervals
if(t1 > tmin) tmin = t1 ;
if(t2 < tmax) tmax = t2 ;
//Exit with no collision as soon as slab intersection becomes empty
if(tmin > tmax) return false ;
}// end for perpendicular to z-axie
vcHit->x = origin.x + tmin * dir.x ;
vcHit->y = origin.y + tmin * dir.y ;
vcHit->z = origin.z + tmin * dir.z ;
return true ;
}// end for intersectWithAABB这个代码我大概的解释下,为了保证,在求交点的时候不发生除0异常,该算法先判断此时的方向向量D的某个分量是否为0,如果是的话,只需要简单的判断就能够知道是否与AABB交叉,因为此时射线是与某个轴平行的。
在上面的代码中,除了一直求三个候选平面的最大t值之外,该算法还一直计算了另外三个非候选平面的最小t值,并且自每次计算之后,判断下此时的交叉点的t值,也就是tmin,是否大于tmax,如果是的话,就说明,该轴上求出的t值并不在AABB盒上(只要简单的在草稿纸上画个图,就应该明白这个),而一旦有一个轴上发生了分离,那么我们就不需要进行下面的步骤了,一个轴上发生了分离,则表示射线与AABB盒不可能发生交叉。
程序实例
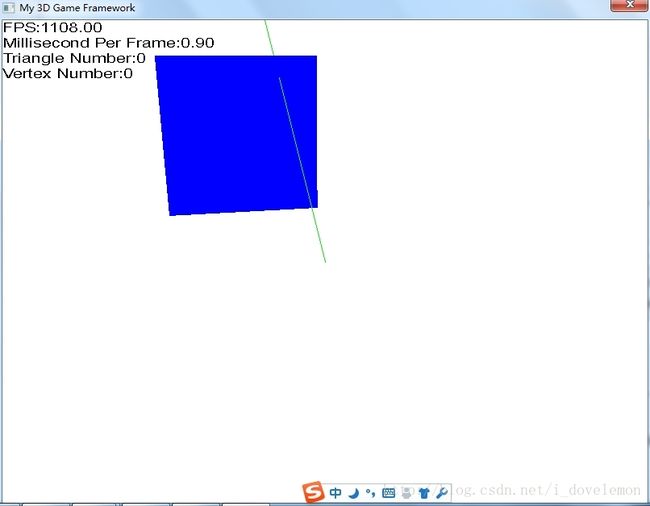
没有交叉前的截图:
交叉之后的图:
好了,今天的文章到此结束。
参考书: Real time collision detection
Graphics Gems I