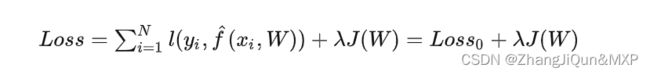神经网络改进:注重空间变化,权重参数调整,正则化, 熵的简单理解
目录
神经网络改进:注重空间变化
将高纬空间映射到地位空间便于表示(供给数据)
将地位空间映射到高纬空间进行分类聚合(达到可分状态(K-means))
神经网络改进:权重参数调整
自注意力机制(数据间关联性)
多注意力机制(加权)
正则化(增加模型参数,不要拟合的太真)
数学上解释正则化的作用
为什么参数小模型会简单
正则化
正则化为什么可以防止过拟合
卷积网络和循环神经网络让我们对神经元展开结构继续改造的能力
transform 让我们对微观结构进行改造
自注意力机制计算序列之间关联权重
多头注意力机制捕获不同维度的特征信息
神经网络通过低纬度空间实现了对高纬复杂流行空间结构的一种编程能力
熵的简单理解:不确定性的度量
对数的应用:
神经网络改进:注重空间变化
将高纬空间映射到地位空间便于表示(供给数据)
将地位空间映射到高纬空间进行分类聚合(达到可分状态(K-means))
神经网络改进:权重参数调整
自注意力机制(数据间关联性)
多注意力机制(加权)
正则化(增加模型参数,不要拟合的太真)
是一种常用的防止机器学习模型过拟合的技术。过拟合是指模型在训练数据上表现得太好,以至于它不能很好地推广到未见过的数据上。正则化通过引入一个惩罚项来限制模型的复杂度,使得模型在尽可能减小训练误差的同时,也要尽量保持模型的简单。
常见的正则化方法有L1正则化和L2正则化:
1. L1正则化(Lasso回归):L1正则化将模型的参数权重的绝对值之和作为惩罚项。这意味着模型的某些参数可能会变为零,从而使得模型更稀疏,也就是说模型会依赖于更少的特征。这也使得L1正则化具有特征选择的功能。
2. L2正则化(岭回归):L2正则化将模型的参数权重的平方和作为惩罚项。这使得模型的参数会被适度地缩小,但是不太可能变为零。这种方法可以防止模型的参数值过大,导致模型过于敏感。
在损失函数中引入这些正则项,模型在训练时不仅要最小化原始的损失函数(如均方误差、交叉熵等),还要尽量使得模型的复杂度(即参数的大小)保持较小。这种权衡使得模型在减小训练误差的同时,也要考虑模型的复杂度,从而防止过拟合。
正则化的选择和调整是一个重要的调参过程,选择合适的正则化方法和参数可以显著地提高模型的泛化性能。
数学上解释正则化的作用
假设我们有一个线性回归模型,其损失函数是均方误差(Mean Squared Error,MSE),表示为:
L(θ) = Σ(yi - θ*xi)^2
其中 θ 是模型的参数,xi 是输入,yi 是真实输出,Σ 是对所有训练样本的求和。
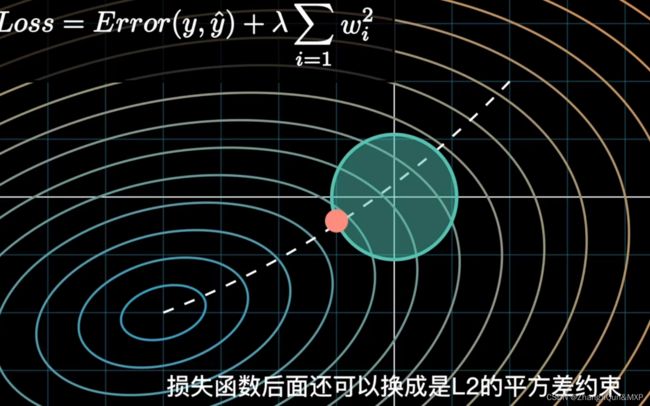
现在我们要在这个损失函数中引入一个正则化项。对于L2正则化(岭回归),我们添加的是参数的平方和;对于L1正则化(Lasso回归),我们添加的是参数的绝对值。我们将正则化参数表示为 λ,那么带有L2正则化的损失函数可以表示为:
L(θ) = Σ(yi - θxi)^2 + λΣθ^2
带有L1正则化的损失函数可以表示为:
L(θ) = Σ(yi - θxi)^2 + λΣ|θ|
现在我们的目标是最小化这个新的损失函数。这意味着我们不仅要使预测值与真实值之间的差异尽可能小,也要使模型的参数尽可能小。因为如果模型的参数较大,那么正则化项就会较大,损失函数就会较大。
这就是正则化如何在数学上鼓励模型保持较小的参数的原理。通过选择合适的正则化参数 λ,我们可以控制模型对拟合数据和保持参数小之间的取舍,从而防止过拟合。
需要注意的是,虽然正则化可以帮助防止过拟合,但如果正则化参数 λ 设置得过大,可能会导致模型过于简单,无法捕捉到数据的复杂性,这就是欠拟合。所以,选择合适的正则化参数是一个重要的任务,通常需要通过交叉验证或其他方式进行。
为什么参数小模型会简单
在机器学习中,模型的参数决定了模型的复杂性和拟合能力。参数的数量和大小都会影响模型的复杂性。
考虑一个线性模型的例子,该模型的形式为y = θ0 + θ1x1 + θ2x2 + ... + θn*xn。其中,θi是模型的参数,xi是输入特征。模型的输出y是输入特征和参数的线性组合。
如果参数θi的绝对值很大,那么对应的特征xi就会对模型的输出产生很大的影响。换句话说,模型对这个特征非常“敏感”。这可能会导致模型过于复杂,对训练数据中的噪声或异常值过度敏感,导致过拟合。
相反,如果参数θi的绝对值较小,那么对应的特征xi对模型的输出的影响就较小。这意味着模型对这个特征不那么敏感,模型的复杂性相对较低。
正则化就是通过添加一个与参数大小相关的惩罚项来鼓励模型保持较小的参数。这可以防止模型过于依赖某个或某些特征,使得模型对输入数据的各个方面都有适当的关注,从而提高模型的泛化能力。
正则化
是一种常用的模型训练方法,它的作用是限制模型的复杂度,以防止过拟合。具体来说,正则化会通过向损失函数中加入一个惩罚项来限制模型的复杂度,其中惩罚项中的参数称为正则化系数。正则化的类型有很多,常见的有 L1 正则化和 L2 正则化。
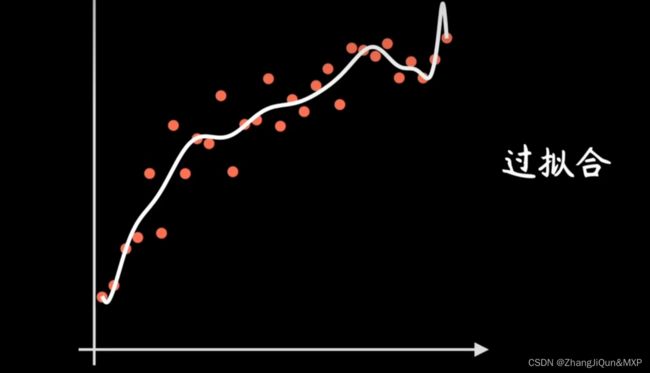
过拟合是模型处于预测结果偏差小而方差大的状态。处于过拟合状态的模型过于细致地记住了训练集的特点,导致对训练集中的噪声敏感,因此泛化能力差,在验证集或测试集效果差。
造成过拟合的原因有几种:(1) 训练数据不足,(2) 训练数据噪音大,(3) 模型过于复杂。
了解了过拟合的原因之后,就可以对症下药,对不同的原因采用不同的方法。
- 对于训练数据不足则通过数据增广的方式来增加训练数据;
- 对于训练数据噪音大,则可以在训练前对数据进行一些清洗工作;
- 对于模型过于复杂,有很多种方法,比如模型剪枝、正则化、dropout等,本文主要讨论正则化,其它方法后续有时间将会陆续讨论。
我们用训练集上的loss来表示当前模型 f^ 和真实映射 f 的差异,loss是模型预测的 y^ 与真实的 y 的差异,即式子(1),其中 W 为当前模型 f^ 的参数, N 为训练集中样本数量。模型训练的过程就是损失最小的过程。
上述loss只考虑了基于训练集的经验风险(表示为 Loss0(W) ),当模型训练使损失最小时,容易造成在训练集上的过拟合。为了缓解过拟合问题,在损失函数中加入描述模型复杂度的正则项 J(W) ,如式子(2),其中 λ 用于控制正则化强度,以权衡经验风险和模型复杂度。正则项的加入,使得损失函数从经验风险转化为结构风险。
总结来说,正则化是通过在损失中引入描述模型复杂度的正则项,把经验风险最小化转化为结构风险最小化,从而防止模型过拟合。
正则化为什么可以防止过拟合
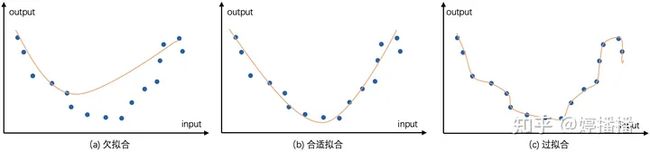
在连续性的世界里,微小变化导致结果变化也是微小的,大变化导致结果变化也大。而当模型过拟合时,微小的输入变化会导致大的输出差异。
造成该现象的原因是过拟合的模型对训练集的数据拟合得很“完美”,对每一个数据都能准确地预测出结果,如图1(c)所示。而训练集中的数据情况复杂,噪声无法避免和异常值,于是就存在一些输入变化小而结果差异大的数据,过拟合的模型对这些数据也能准确输出,于是导致上述现象。
过拟合的模型既要满足连续性角度的输入变化大结果变化大这一规律,也要顾忌训练集中所有的数据,即输入变化小结果变化大的情况,在输入变化有大有小的情况下都要保证输出变化大,只能通过大的参数来实现。
正则化通过在损失项中加入对模型复杂度的描述,从而对模型参数增加了限制,因此增加了模型对每个数据都准确得到结果的难度,从而防止过拟合。
如何防止过拟合(1)-正则化 - 知乎
卷积网络和循环神经网络让我们对神经元展开结构继续改造的能力
transform 让我们对微观结构进行改造
自注意力机制计算序列之间关联权重
多头注意力机制捕获不同维度的特征信息
神经网络通过低纬度空间实现了对高纬复杂流行空间结构的一种编程能力
熵的简单理解:不确定性的度量
对数的应用:
应用一:二进制编码
一位二进制数,可以表示2个数字,0或1。
二位二进制数,可以表示4个数字,即00,01,10,11。 十进制下为0,1,2,3
三位二进制数,可以表示8个数字,即000,001,010,011,100,101,110,111。十进制下为0,1,2,3,4,5,6,7
我们可以看到规律: