神经网络——神经元
神经网络的概念在此不做过多阐述,其应用领域包括:
- 分类——即预测输入向量的类别;
- 模式匹配——即产生与给定输入向量最佳关联的模式;
- 模式完成——其目的是完成给定输入向量的缺失部分;
- 优化——即找到优化问题中参数的最优值;
- 控制——给定一个输入向量,得到建议的合适行为;
- 函数拟合 / 时间序列模型——学习输入与输出之间的函数关系;
- 数据挖掘——挖掘数据背后的模式(信息)
. . . . . . . ....... .......
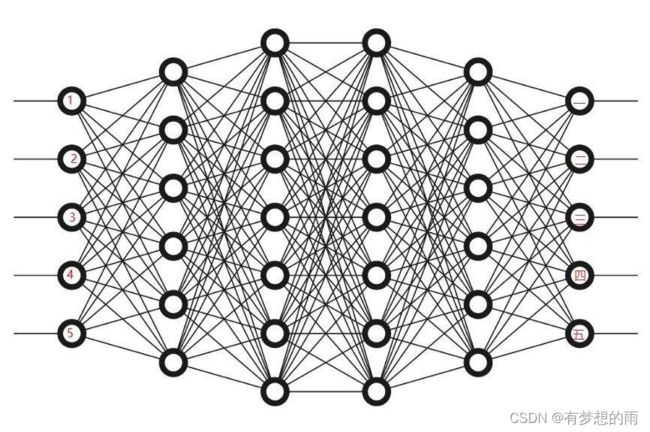
一个神经完了实现的是一个从 R I \mathbb R^I RI 到 R K \mathbb R^K RK 非线性映射,如: f N N : R I → R K f_{NN}:\mathbb R^I\to\mathbb R^K fNN:RI→RK,其中, I , K I,K I,K 分别为输入空间和目标(输出)空间的维数,而 f N N f_{NN} fNN 是一个由一组非线性函数构成的复杂函数,每个神经元为一个函数操作。
神经元
一个神经元,依靠激活函数,实现从 R I \mathbb R^I RI 到 [ 0 , 1 ] 或 [ − 1 , 1 ] [0,1]或[-1,1] [0,1]或[−1,1]的非线性映射(取决于激活函数的选择)。将其输入记为 Z Z Z,每一维度为 z i z_i zi,对应权重为 v i v_i vi (可实现对输入信号的增强或削弱),输入信号受阈值(or 偏差) θ \theta θ 的影响,使用激活函数 f A N f_{AN} fAN 得到输出 o o o。一般的单个神经元示意图如下:
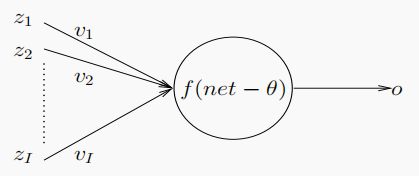
计算节点输入信号
-
以输入信号的权重之和为节点输入信号的神经元被称为求和单元 ( s u m m a t i o n u n i t s , S U ) (summation\;units,SU) (summationunits,SU);即 n e t = ∑ i = 1 I z i ⋅ v i = Z ⋅ V \displaystyle net=\sum^I_{i=1}z_i\cdot v_i=Z\cdot V net=i=1∑Izi⋅vi=Z⋅V。
若以向量形式表达,两向量越相似,则他们的点积越大,因为: Z ⋅ V = c o s ( Z , V ) ∣ ∣ Z ∣ ∣ ⋅ ∣ ∣ V ∣ ∣ \displaystyle Z\cdot V=\frac{cos(Z,V)}{||Z||\cdot||V||} Z⋅V=∣∣Z∣∣⋅∣∣V∣∣cos(Z,V),故点积可被视为相似度度量。 -
以输入信号的高阶权重组合为节点输入信号的神经元被称为求积单元 ( p r o d u c t u n i t s , P U ) (product\;units,PU) (productunits,PU),有信号增强的功能;即 n e t = ∑ i = 1 I z i v i \displaystyle net=\sum^I_{i=1}z_i^{v_i} net=i=1∑Izivi。
-
神经元直接的均值-方差连接,其输入有两个权值链接,一个代表连接该输入上的均值,另一个代表方差,以 W = ( w 1 , w 2 , ⋯ , w n ) , V = ( v 1 , v 2 , ⋯ , v n ) W=(w_1,w_2,\cdots,w_n),V=(v_1,v_2,\cdots,v_n) W=(w1,w2,⋯,wn),V=(v1,v2,⋯,vn),则 n e t = ∑ i = 1 n ( z i − w i v i ) 2 \displaystyle net=\sum^n_{i=1}(\frac{z_i-w_i}{v_i})^2 net=i=1∑n(vizi−wi)2,其示意图如下:

若使用该类型的连接方式,则激活函数选择高斯函数较好
激活函数
神经元的信号流图
信号流图是一个由有向连接的互连接点组成的网络。一个典型的节点 j j j 有一个相应的节点信号 x j x_j xj;一个典型的有向连接从某个节点 j j j 开始,到节点 k k k 结束,并有相应的传递函数或传递系数以确定节点 k k k 的信号 y k y_k yk 依赖于节点 j j j 的信号之间的方式,典型的链接如下:
1.突触连接:一个信号节点流到另一个信号节点,输入输出关系为线性;
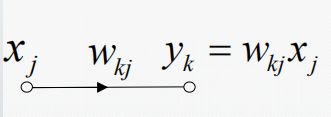
2.激活连接:一个信号节点流到另一个信号节点,输入输出关系为函数(一般非线性);
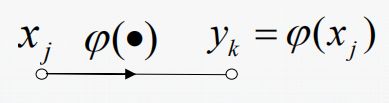
3.扇入连接:多个信号节点流到另一个信号节点,输出信号是输入信号的累加;
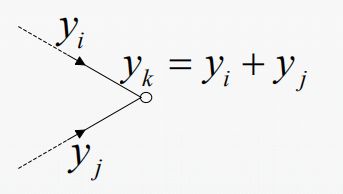
4.扇出连接:一个信号节点流到多个信号节点,每个输出信号都等于输入信号。

一个感知器的信号流图如下所示:
其输出表达为: y k = φ ( v k ) = φ ( ∑ i = 0 m x i ⋅ w k i ) \displaystyle y_k=\varphi(v_k)=\varphi(\sum^m_{i=0}x_i\cdot w_{ki}) yk=φ(vk)=φ(i=0∑mxi⋅wki)
神经元的几何解释
单个神经元可无误差的实现线性可分问题(即神经元可以通过一个超平面实现一个高维空间的线性分割)。即将输入空间分割为: ∑ i z i ⋅ v i − θ > 0 \displaystyle \sum_i z_i\cdot v_i-\theta>0 i∑zi⋅vi−θ>0 和 ∑ i z i ⋅ v i − θ < 0 \displaystyle \sum_i z_i\cdot v_i-\theta<0 i∑zi⋅vi−θ<0 两部分,如下图所示:
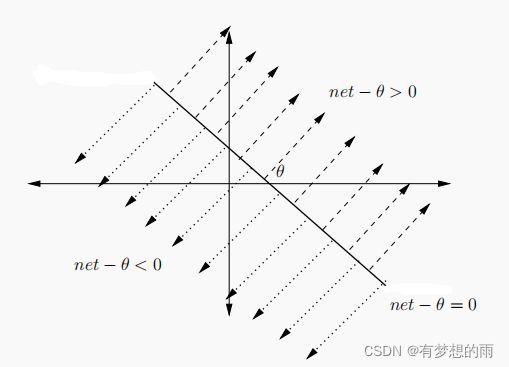
单个神经元可以解决线性可分问题,如 Bool 函数中的 或、且,但不能解决亦或问题(可使用多个神经元解决)。
神经元的学习
神经元(神经网络)的学习能力可视为:神经元如何实现自动决定权重 v i v_i vi 和阈值 θ \theta θ 的值? 神经元通过给定的数据来学习权重 v i v_i vi 和阈值 θ \theta θ 的值,不断的进行权重和阈值的调整,直到满足指定的准则(要求)。主要的三种学习方法如下:
1. 监督学习:给神经元一组数据集(即一组输入向量与与之对应的目标(渴望输出)),其目标是调整权值,使得神经元得到的输出与目标输出之间的误差最小;eg.分类
2. 无监督学习:给定一组没有辅助信息的数据,想让神经元(神经网络)去发现输入数据背后的模式或特征;多用于聚类问题。
3.强化学习:嘉奖神经元良好的行为,而对坏的行为进行处罚。
增广向量(Augmented Vectors)
在之前的表述中, n e t = ∑ i = 1 I z i ⋅ v i \displaystyle net=\sum^I_{i=1}z_i\cdot v_i net=i=1∑Izi⋅vi,为方便后续的表述,引入增广向量,即使 v I + 1 = − θ , z I + 1 = 1 v_{I+1}=-\theta,z_{I+1}=1 vI+1=−θ,zI+1=1,
则使得 n e t = ∑ i = 1 I + 1 z i ⋅ v i \displaystyle net=\sum^{I+1}_{i=1}z_i\cdot v_i net=i=1∑I+1zi⋅vi,即可使神经元的输出可表示为: o = f ( n e t ) o=f(net) o=f(net)。
梯度下降(Gradient Descent,GD)
梯度下降法不是最早提出的对神经网络进行训练的方法,但却是使用最多的一个,定义神经元的误差函数为 ε = 1 2 ∑ p = 1 P T ( t p − o p ) 2 \displaystyle\varepsilon=\frac{1}{2}\sum^{P_T}_{p=1}(t_p-o_p)^2 ε=21p=1∑PT(tp−op)2,其中, t p , o p t_p,o_p tp,op 分别表示第 p p p 个输入向量的目标输出和神经元的实际输出, P T P_T PT表示总的输入向量的个数。
GD的目的是找到使 ε \varepsilon ε 最小的权重的值,这可以利用 ε \varepsilon ε 在权重空间的梯度计算得到(使权重向量沿负梯度方向移动),如下图所示:
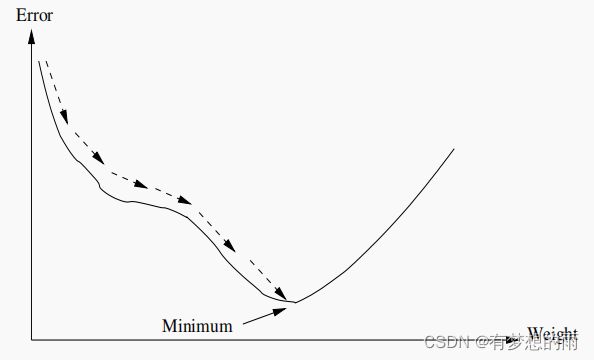
权重更新方式: v i ( t ) = v i ( t − 1 ) + △ v i ( t ) \displaystyle v_i(t)=v_i(t-1)+\bigtriangleup v_i(t) vi(t)=vi(t−1)+△vi(t),其中 △ v i ( t ) = η ⋅ ( − ∂ ε ∂ v i ) \displaystyle\bigtriangleup v_i(t)=\eta\cdot(-\frac{\partial\varepsilon}{\partial v_i}) △vi(t)=η⋅(−∂vi∂ε),
其中 − ∂ ε ∂ v i = ( t p − o p ) ⋅ ∂ f ∂ n e t p ⋅ z i , p \displaystyle-\frac{\partial\varepsilon}{\partial v_i}=(t_p-o_p)\cdot \frac{\partial f}{\partial net_p}\cdot z_{i,p} −∂vi∂ε=(tp−op)⋅∂netp∂f⋅zi,p, η \eta η 为学习率, z i , p z_{i,p} zi,p 为输入的第 p 个向量中的第 i 维的数据。