【C++刷题集】-- day5
目录
选择题
单选
编程题
统计回文⭐
【题目解析】
【解题思路 - 穷举】
【优化】
连续最大和⭐
【题目解析】
【解题思路】
【空间优化】
选择题
单选
int x = 1;
do {
printf("%2d\n", x++);
} while (x--);
1
无任何输出
2
陷入死循环
正确答案：
解析：
- do while循环是先执行do再执行while的条件判断。
- x++：后置++，先使用x的值然后再x + 1，所以此处是输出时可以说恒等于1，where判断的时候x恒等于2进行x--等于1，于是陷入死循环。
- 格式化输出：
来源printf 函数转换说明完整格式详解-CSDN博客
精度：
- 对于整型数据类型（如：int、long、short），精度修饰符没有任何作用，会被忽略。
- 对于浮点数数据类型（如：float、double），可以使用格式说明符%.nf来指定输出的小数位数。例如：%.2f表示保留两位小数。
- 对于字符型数据类型（如：char），精度修饰符也没有任何作用，会被忽略。
- 对于字符串类型（如：char*），可以使用格式说明符%.ns来指定输出的字符个数。例如：%.5s表示只输出字符串的前五个字符。
数据长度与字段宽度与精度的关系：
- 字符串：%m.ns
- 字符串长度 > n > m：此时m的作用失效，是只受n的控制。
const char* str = "abcdefg"; printf("%2.5s\n", str); //abcde- m > n：是右对齐补空格。
const char* str = "abcdefg"; printf("%5.2s\n", str); // ab- n > 字符串长度：作用与%s一样。
const char* str = "abcdefg"; printf("%5.100s\n", str); //abcdefg- 浮点数：%m.nf
- m < 整数部分 + n：此时m的作用失效，是只受n的控制。
float number = 202383.1415; printf("%4.1f\n", number); //202383.1- m > 整数部分 + n：是右对齐补空格。
float number = 202383.1415; printf("%10.1f\n", number); // 202383.1- n > 小数位数：注意，在指定精度时要确保实际数据长度大于精度才有意义，否则可能会导致不必要的错误或者无法预料的结果。
float number = 202383.1415; printf("%20.10f\n", number); // 202383.1406250000
----------------------------------------------
10,4
4,4
9,9
9,4
正确答案：
解析：
- sizeof 求变量对应类型所占字节数：C语言字符串结尾最后会自动补充一个'\0'，所以为：9 + 1。
- strlen求字符串的有效长度不包含 '\0' 在内：该字符串第5个字符为'\0'，所以为：4。
----------------------------------------------
char p1[15] = "abcd", * p2 = "ABCD", str[50] = "xyz";
strcpy(str + 2, strcat(p1 + 2, p2 + 1));
printf("%s", str);正确答案：
解析：
- char p1[15] = "abcd"；一维数组。
- char * p2 = "ABCD"; 指向常量字符串，该字符串中的内容是不能被修改的，存储在代码段。
- char str[50] = "xyz"；一维数组。
字符串函数功能：
- strcpy(dest, src)：将src字符串中的内容拷贝到dest所在的空间中，最后返回dest。（注意：dest的空间大小一定要能够存的下src中的字符总数，否则程序会崩溃）
- strcat(dest, src)：将src字符串中的内容拼接在dest字符串之后，最终返回dest。（注意：dest空间一定要能够容忍下src拼接进来的字符，否则程序会崩溃）
strcat(p1 + 2, p2 + 1)： "cd" 拼接 "BCD" 为 "cdBCD" 。
strcpy(str + 2, "cdBCD")：将 "cdBCD" 拷贝到str+2的位置为 "xycdBCD" 。
----------------------------------------------
#include
void main() {
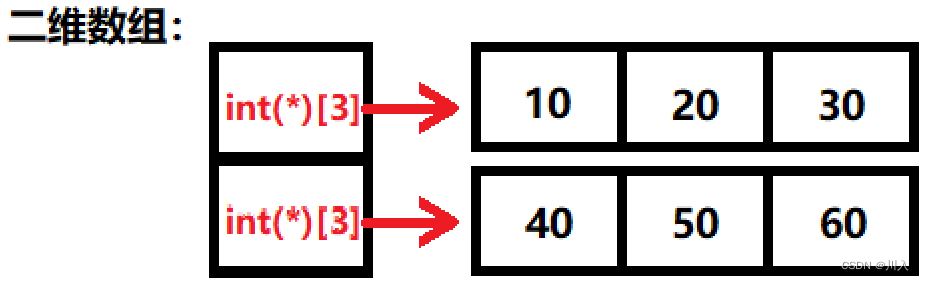
int n[][3] = { 10,20,30,40,50,60 };
int(*p)[3];
p = n;
cout << p[0][0] << "," << *(p[0] + 1) << "," << (*p)[2] << endl;
} 正确答案：
解析：
二维数组的行可以省略，所以n是两行三列的二维数组。
int(*p)[3]：是数组指针，本质是一个指针，该指针只能指向具有3个int类型元素的一段连续空间。
数组名表示的就是数组搜元素的地址，此处二维数组n的每一个元素实际上就是一个一维数组int[3]，n的二维数组中，首元素的地址就是int(*)[3]。
- p[0][0] == *(*(p + 0) + 0)
- *(p[0] + 1) == *(*(p + 0) + 1)
- (*p)[2] == *(*(p + 0) + 2)
所以，最后显示的全是第0行，第一个元素，第二个元素。第三个元素。
----------------------------------------------
C++程序中的main()函数必须放在程序的开始部分。
C++程序的入口函数是main函数。
在C++程序中，要调用的函数必须在main()函数中。
正确答案：
解析：
- main函数可以放在任何位置，只要不放在某一个函数的定义之内即可。
- 在C / C++中，函数的定义是不能嵌套的。
----------------------------------------------
#include
using namespace std;
char fun(char x, char y) {
if (x < y)
return x;
return y;
}
int main() {
int a = '1', b = '1', c = '2';
cout << fun(fun(a, b), fun(b, c));
return 0;
} 正确答案：
解析：
可以看出fun函数的算法是拿出x和y中的最小值。
----------------------------------------------
pa是一个具有5个元素的指针数组，每个元素是一个int类型的指针。
pa是一个指向数组的指针，所指向的数组是5个int类型的元素。
pa[5]表示某个数的第5个元素的值。
pa是一个指向某个数组中第5个元素的指针，该元素是int类型的变量。
正确答案：
解析：
int* pa[5]：pa是一个指针数组，该数组中的每个元素都是 int* 类型的指针。
----------------------------------------------
struct One {
double d;
char c;
int i;
}
struct Two {
char c;
double d;
int i;
}正确答案：
解析：
结构体的大小计算遵循结构体的对齐规则：
结构体的第一个成员放在结构体变量在内存中存储位置的0偏移处开始
从第2个成员往后的所有成员，都要放在一个对齐数（成员的大小和默认对齐数的较小值）的整数的整数倍的地址处，VS中默认对齐数为8
结构体的总大小是结构体的所有成员的对齐数中最大对齐数的整数倍。
如果嵌套了结构体的情况，嵌套的结构体对齐到自己的最大对齐数的整数倍处，结构体的整体大小就是所有最大对齐数（含嵌套结构体的对齐数）的整数倍
#注：VS中的默认对齐数为8，不是所有编译器都有默认对齐数，当编译器没有默认对齐数的时候，成员变量的大小就是该成员的对齐数。（Linux中就没有默认对齐数概念）
补充：
#结构体为什么要内存对齐？
- 平台原因(移植原因)：
- 不是所有的硬件平台都能访问任意地址上的任意数据的；某些硬件平台只能在某些地址处取某些特定类型的数据，否则抛出硬件异常。
- 性能原因：
- 数据结构(尤其是栈)应该尽可能地在自然边界上对齐。原因在于，为了访问未对齐的内存，处理器需要作两次内存访问；而对齐的内存访问仅需要一次访问。
总体来说：结构体的内存对齐是拿空间来换取时间的做法。
----------------------------------------------
(((a+i)+j)+k)+l)
*(*(*(*(a+i)+j)+k)+l)
(((a+i)+j)+k+l)
((a+i)+j+k+l)
正确答案：
解析：
既然是要访问用来引用，那肯定需要解引用，已知：a[1] == *(a + 1)。
- *(*(*(*(a+i)+j)+k)+l) == *(*(*(a+i)+j)+k)[l] == *(*(a+i)+j)[k][l] == *(a+i)[j][k][l] == a[i][j][k][l]
----------------------------------------------
预处理
编译
链接
执行
正确答案：
解析：
知识铺垫：
现在所使用的编译器为满足复杂的软件开发需求，如：Linux下使用的GCC，是被称为 编译器套装 ，是因为它不仅仅包含了一个编译器，而是由多个编译器及相关工具组成的一个完整的编程环境。除了g++、gcc和gfortran等编译器之外，GCC还包括了预处理器、汇编器、链接器等多个工具。这些工具协同工作，可以将源代码转换成可执行文件或库文件。
因此，GCC被称为编译器套装是因为它提供了完整的编译、链接和调试工具链，能够满足复杂的软件开发需求。
（VS2019、DEV C++等，被称作集成开发环境-IDE，其具备编辑、预处理、编译、汇编、链接、调试、运行）
阶段：
- 编辑（编辑器）：将程序员 编写源代码 保存到文件中，并进行必要的格式化处理。
- 预处理（编译器）：完成包含的 头文件的展开 、 注释删除 、 define宏替换 、 条件编译 等，最终形成 xxx.i 文件。头文件是不参与编译的，因为在预处理阶段已经将头文件展开了，编译只对源文件进行编译。
链接之前每个源文件都是独立的单元，它们之间并没有直接的联系。在链接阶段，编译器才会将这些独立的目标文件链接在一起，生成可执行文件或者共享库。
使用条件编译和#pragma once：能够防止一个源文件内多次包含同一个头文件，即能够确保在多个源文件下，各个源文件对于同一个头文件各自只包含一次。
- 编译（编译器）：完成 词法分析 、 语法分析 、 语义分析 、 符号汇总 等（编译器对源代码语法规则进行检测，如此才可以交付后续转换为可执行代码），检查无误后将代码翻译成 汇编 指令，最终形成 xxx.s 文件。
汇编（编译器）：将 汇编 指令转换成 二进制 指令，形成 符号表 ，最终形成 xxx.o 文件。
链接（编译器）：将生成的各个 xxx.o 文件进行 链接 ， 合并段表 、 符号表的合并和重定位 ，最终形成 .exe(.out) 可执行程序。
运行（计算机执行）： .exe(.out) 可执行程序会被加载到内存中，并按照预定的逻辑进行计算和处理。
各类阶段错误：
- 预处理错误：程序编译之前发生的错误，这些错误通常与头文件、宏定义、条件编译等相关。
- 找不到头文件：当程序中引用了不存在的头文件时，会发生找不到头文件的错误。
- 宏定义问题：当程序中使用了未定义或重复定义的宏时，会发生宏定义问题。
- 条件编译问题：当程序中使用了不正确的条件编译语句时，会发生条件编译问题。
- 编码格式问题：当程序中出现了不支持的编码格式时，会发生编码格式问题。
- 编译错误：编译器会检测代码中存在的错误。如有错误，则会导致程序无法通过编译，并给出相应的错误提示信息，指出哪一行代码存在问题以及具体的错误类型。
- 语法错误(Syntax Error)：代码中存在拼写错误、缺少分号、括号不匹配等语法问题。
- 未定义变量(Undefined Variable Error)：在程序中引用了未定义的变量。
- 类型错误(Type Error)：代码中使用了不兼容的数据类型，例如：将字符串赋值给整数变量。
- 函数调用错误(Function Call Error)：函数调用参数数量不匹配、参数类型不正确等问题。
- 头文件引用错误(Header File Error)：头文件不存在或者路径不正确等问题。
- 环境配置错误(Environment Configuration Error)：编译器或者开发环境配置不正确导致编译失败。
- 内存错误(Memory Error)：程序访问了无效的内存地址，例如：空指针引用等。
- 重复定义(Redeclaration Error)：在同一作用域中重复定义变量、函数等。
- 编译器警告(Compiler Warning)：这种警告通常是编译器发现了代码中可能存在问题或潜在风险，例如：未使用的变量、类型转换可能会丢失精度等，出现在编译阶段。
- 链接错误：也称为连接错误，链接器将多个目标文件和库文件合并成一个可执行程序，并需要解决符号引用和符号定义之间的关系。如果检测到错误，链接器将停止链接并显示错误消息。
- 未定义符号(Undefined Symbol Error)：使用未定义的函数或变量。
- 手误拼写了变量、函数或对象的名称。
- 没有包含必要的头文件。
- 在使用外部库时，没有正确地链接库文件。
- 在多个源文件中使用同一个全局变量，但只在其中一个源文件中进行了定义。
- 重复定义符号(Duplicate Symbol Error)：多次定义同一个函数或变量。
- 头文件重复包含：如果多个源文件都包含同一个头文件，并且该头文件中定义了全局变量或函数，那么在编译时就会出现重复定义符号错误。
- 全局变量重复定义：如果多个源文件中都定义了同名的全局变量，并且这些变量的作用域超出了各自的源文件范围，那么在链接时就会出现重复定义符号错误。
- 函数重复定义：如果多个源文件中都定义了同名的函数，并且这些函数的作用域超出了各自的源文件范围，那么在链接时就会出现重复定义符号错误。
多文件 (嵌套文件包含) 编译的重点问题 -> 解决方案 在头文件中只声明变量和函数，而不要定义它们，在一个源文件中定义变量和函数，并将其它源文件需要使用的声明放在头文件中。 使用 static 关键字来限制变量的作用域，避免在不同源文件中产生冲突。 使用 条件编译 和 #pragma once 预处理指令来避免头文件被重复引用。 使用 命名空间 等技术来避免符号冲突问题。 - 缺少库文件：使用未包含或版本不兼容的库文件。
- 符号冲突：不同目标文件包含具有相同名称但实现不同的函数或变量。
- 重复定义变量或函数名：在程序中定义了两个或多个同名的变量或函数。
- 重复定义标签：在程序中定义了两个或多个同名的标签。
- 命名规则不规范：在程序中使用了与汇编器保留字相同的名称，导致汇编器无法识别。
- 头文件包含重复定义的内容：头文件中包含了与当前程序中已有的变量、函数等同名的内容。
- 模块之间命名冲突：在一个大型项目中，不同模块之间可能会出现命名冲突问题。
- 宏定义名称重复：在宏定义时使用了与已有宏定义相同的名称。
- 数据对齐错误：在不同的目标文件中使用了不同的数据对齐方法。
- 访问未对齐的地址：当访问一个未按照对齐方式对齐的内存地址时，会出现数据对齐错误。
- 结构体成员对齐不一致：结构体成员在默认情况下按照其自身大小进行对齐，但可以通过编译器指定结构体成员的对齐方式。如果不同结构体成员的对齐方式不一致，可能会导致数据对齐错误。
- 指针类型不匹配：一个指针指向的内存区域按照某种对齐方式进行对齐时，如果将该指针强制转换成另一种类型的指针，而新类型的对齐方式与原先的不同，就可能会导致数据对齐错误。例如：将一个按照8字节对齐方式进行对齐的double类型数组强制转换成int类型数组的指针，可能会导致数据对齐错误。
- 编译器优化：编译器在进行优化时可能会改变内存布局，从而导致数据对齐错误。
- 跨平台移植：在跨平台移植时，由于不同平台的字节顺序、大小和对齐方式可能不同，需要特别注意数据对齐问题。
- 运行错误：程序在运行时发生了异常或错误，这种错误可能会导致程序崩溃、停止工作或产生不正确的结果。
- 空指针引用：程序试图访问一个空指针时，会发生空指针引用错误。
- 没有初始化指针变量就使用它。
- 对已经释放的内存进行操作。
- 函数返回了一个空指针，但没有进行检查就使用它。
- 在结构体中访问了一个不存在的成员变量。
解决措施 使用指针变量之前，始终确保对其进行初始化。 释放内存之后，将指针变量设置为 NULL。 使用函数返回值之前，始终检查其是否为空指针。 访问结构体成员变量之前，始终检查该成员是否存在。 - 数组越界：程序试图访问一个超出数组边界的元素时，会发生数组越界错误。
- 内存泄漏：程序分配了一块内存但没有释放时，会发生内存泄漏错误。
- 忘记释放动态分配的内存：通过 malloc 或 new 等函数动态分配了内存，但没有及时释放，会导致内存泄漏。
- 指针操作不当：存在指针操作不当的情况，如：指针未初始化、指针越界、重复释放等，会导致内存泄漏。
- 异常处理不当：存在异常处理不当的情况，如：在抛出异常前未释放资源等，也会导致内存泄漏。
解决措施 在使用完动态分配的内存后及时调用free或delete等函数进行释放。 对于指针操作，要确保指针正确初始化，并且避免指针越界、重复释放等情况。 在异常处理中及时进行资源清理，并且避免在抛出异常前未释放资源等情况。 使用智能指针等自动化管理内存的方式来减少手动管理带来的风险。 - 栈溢出：程序使用过多的栈空间时，会发生栈溢出错误。
- 递归调用：递归函数没有正确终止条件或者递归深度太大，会导致栈溢出。
- 局部变量过多：函数中定义了太多的局部变量，会导致栈空间不足导致栈溢出。
- 缓冲区溢出：程序尝试向缓冲区写入超过其大小的数据，会导致栈溢出。
- 函数调用嵌套过深：函数调用嵌套层数太多，会导致栈空间不足。
解决措施 确保递归函数有正确的终止条件，并且递归深度不会太大。 尽可能减少局部变量的数量，并且使用动态内存分配来代替数组等静态分配方式。 对于缓冲区操作，要确保输入数据不会超过缓冲区大小，并且使用安全的字符串处理函数（如：strcpy_s）来代替不安全的函数（如：strcpy）。 合理设计程序结构，避免函数嵌套层数过深。 - 除0错误：程序试图将一个数除以零时，会发生除零错误。
对于函数未定义的错误：
函数未定义属于链接错误。在C++中，当我们调用一个函数时，编译器会在当前文件或外部文件中查找该函数的定义。如果找不到该函数的定义，编译器就会报 "未定义的引用" 错误，并停止编译。这时，我们需要检查是否正确包含了相关头文件、是否正确链接了相关库文件、是否正确实现了该函数等。
补充：
对于#include 引入源文件，一般情况下是不建议的，而是应该包含对应的头文件。
- 引入源文件缺陷：
- 编译时间增加：当一个头文件被多个源文件包含时，每个源文件都需要重新编译该头文件，这会增加编译时间。
- 命名空间污染：如果被包含的头文件定义了全局变量或函数，那么这些定义将出现在包含它的每个源文件中，可能导致命名冲突和意外行为。
- 不必要的依赖关系：当一个头文件被包含到多个源文件中时，这些源文件之间就会出现不必要的依赖关系。如果修改了这个头文件，所有依赖它的源文件都需要重新编译。
- 应该遵循规则：
- 只包含必要的头文件。
- 在头文件中使用前置声明 (forward declaration) 而不是包含其他头文件来声明类或函数。
- 使用命名空间避免全局命名冲突。
- 将常用的头文件放在预编译头 (precompiled header) 中以提高编译速度。
---------------------------------------------
编程题
统计回文⭐
统计回文_牛客题霸_牛客网 (nowcoder.com)
【题目解析】
回文判断：正读和反读都一样的字符串。
【解题思路 - 穷举】
#include
#include
using namespace std;
// 判断是否是回文
bool IsCircle(const string& s)
{
size_t begin = 0;
size_t end = s.size() - 1;
while (begin < end)
if (s[begin++] != s[end--])
return false;
return true;
}
int main()
{
// 时间复杂度：O(n^2)
// 空间复杂度：O(n)
string str, sub;
getline(cin, str);
getline(cin, sub);
size_t count = 0;
for (size_t i = 0; i <= str.size(); ++i)
{
// 将字符串2插入到字符串1的每个位置，再判断是否是回文
string tmp = str;
tmp.insert(i, sub);
if(IsCircle(tmp))
++count;
}
cout << count << endl;
return 0;
}
// 64 位输出请用 printf("%lld") 【优化】
使用暴力求解方式计算，使用拼接实现两个字符串的插入合并，避免insert(其需要移动)，采取空间换时间，再将其进行判断是否符合回文。
#include
#include
using namespace std;
// 判断是否为回文
bool IsCircle(const string& s)
{
size_t begin = 0;
size_t end = s.size() - 1;
while (begin < end)
if (s[begin++] != s[end--])
return false;
return true;
}
int main()
{
// 时间复杂度：O(n^2)
// 空间复杂度：O(n)
string str;
string sub;
getline(cin, str);
getline(cin, sub);
size_t count = 0;
string tmp;
for(size_t index = 0; index <= str.size(); index++) // index是sub插入的位置
{
// 拼接 - 避免insert(其需要移动)，采取空间换时间
tmp = str.substr(0, index);
tmp += sub;
tmp += str.substr(index);
// 验证是否为回文
if(IsCircle(tmp))
++count;
}
cout << count << endl;
return 0;
}
// 64 位输出请用 printf("%lld") 连续最大和⭐
连续最大和_牛客题霸_牛客网 (nowcoder.com)
【题目解析】
本题是一个经典的动规问题，简称dp问题。
【解题思路】
状态方程式： max(dp[i]) = max(dp[i-1] + arr[i], arr[i]);#include
#include
#include
using namespace std;
int main()
{
// 时间复杂度：O(n)
// 空间复杂度：O(n)
int n = 0;
cin >> n;
vector nums;
nums.reserve(n);
while(n--)
{
int num;
cin >> num;
nums.push_back(num);
}
vector dp(nums.size(), 0);
dp[0] = nums[0];
for(size_t i = 1; i < nums.size(); i++)
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
cout << *max_element(dp.begin(), dp.end()) << endl;
return 0;
}
// 64 位输出请用 printf("%lld") 【空间优化】
将一维数组变为一个元素，并保证其内部，在执行中使用为执行部分的最大值。
#include
#include
#include
using namespace std;
int main()
{
// 时间复杂度：O(n)
// 空间复杂度：O(1)
int n = 0;
cin >> n;
vector nums;
nums.reserve(n);
while(n--)
{
int num;
cin >> num;
nums.push_back(num);
}
int ret_max = -INT_MAX; // 取一个很小很小的值
int tmp_max = 0; // 对应元素的最大值 - 第0个元素最大值为0
for(auto val : nums)
{
int next = tmp_max + val;
if(ret_max < next)
ret_max = next;
if(next < 0)
next = 0;
tmp_max = next;
}
cout << ret_max << endl;
return 0;
}
// 64 位输出请用 printf("%lld")