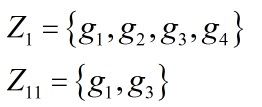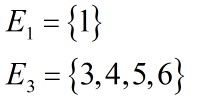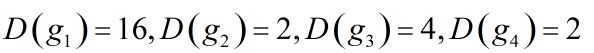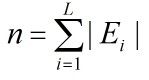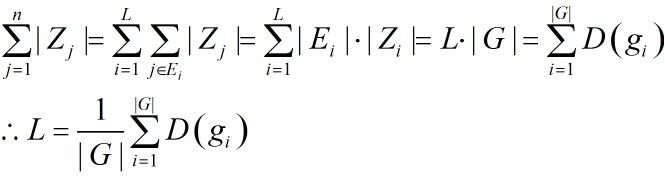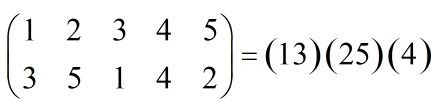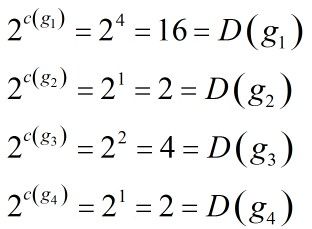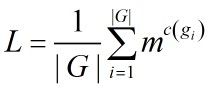Burnside引理和polay计数学习小记
在组合数学中有这样一类问题,比如用红蓝两种颜色对2*2的格子染色,旋转后相同的算作一种。有多少种不同的染色方案?我们列举出,那么一共有16种。但是我们发现,3,4,5,6是同一种,7,8,9,10是用一种,11,12是同一种,13,14,15,16是同一种,也就是只有6种本质上不同的染色。小规模我们可以列举所有方案然后再选择,大规模的时候是很难列举所有方案的。下面,我们说明用Burnside引理和polay计数来解决这类问题。
一、置换群G:即指所有的置换。上面的例子中置换只有4种,即旋转0、90、180和270度。其中G的大小记为|G|=4。
二、(1)对于每个元素K,这里的K满足1<=k<=16,G中使得K保持不变的置换组成的全体,称为![]() 。比如四种置换都可以使得1保持不变,而只有第一种和第三种置换使得11保持不变,所以我们有(G中的元素用g来表示):
。比如四种置换都可以使得1保持不变,而只有第一种和第三种置换使得11保持不变,所以我们有(G中的元素用g来表示):
(2)对于每个元素K,在四种置换的作用下依次得到的元素称作K在G下的轨迹,表示为![]() ,代表一个等价类。比如1在四种置换下都得到1,3在四种置换下依次得到3,4,5,6。所以我们有:
,代表一个等价类。比如1在四种置换下都得到1,3在四种置换下依次得到3,4,5,6。所以我们有:
我们发现在同一个等价类中的元素的等价类都是一样的,比如3,4,5,6的等价类都是跟3一样的。在这里我们给出一个公式,自己计算下显然成立:
四、接下来我们计算每个元素在各个置换下不变的次数总和。如下图所示。
由上图可得到(注意上图是用a来表示置换的,我们都是用的g),比如1在第一种置换下没有变,那么![]() ,且在第一种置换下16种都没有变,第二种置换下只有1、2没有变,第三种置换下只有1,2,11,12没有变,第四种置换下只有1、2没有变,那么有:
,且在第一种置换下16种都没有变,第二种置换下只有1、2没有变,第三种置换下只有1,2,11,12没有变,第四种置换下只有1、2没有变,那么有:
其实我们有下面的式子成立:
下面,我们用n来表示总的元素个数,上面n=16,我们用|G|来表示置换个数,上面|G|=4。我们设有L个等价类(我们在上面说了,比如3,4,5,6的等价类都是一样的,上面其实只有5个等价类,{1},{2},{3,4,5,6},{11,12},{13,14,15,16}),我们有:
所以,
这个就是著名的Burnside引理。注意这里的L其实就是我们要求的不同的染色方案的数目。因为L代表的是不同的等价类,同一个等价类就好比是一种染色。我们得到L=(16+2+4+2)/4=6,跟一开始我们得到的答案是一样的。使用这个引理计算时,第一步求出所有的置换,第二步计算每种置换下的不变元素的个数。但是,我们发现,有时候第二步的这个计算是不那么容易的。下面我们说polay定理。
五、我们首先说明循环节是个啥。
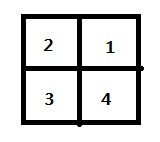
比如对于一个n=5,在某一种置换下(1,2,3,4,5)变成了(3,5,1,4,2),我们将其记为(13)(25)(4),即该置换的循环节为3。也就是两个置换节之间是不相交的。对于上面的那个问题,我们对四个方格标号1,2,3,4。
构造置换:
我们发现,![]() 的同一个置换节中的元素用同一种颜色(我们现在假设用m种颜色,刚才m=2)染色得到的方案数
的同一个置换节中的元素用同一种颜色(我们现在假设用m种颜色,刚才m=2)染色得到的方案数![]() 就是在上面在
就是在上面在![]() 置换下不变的元素数:
置换下不变的元素数:
由此我们得到:
这就是举世闻名的polay定理。用这个定理计算,我们只需要找到每个置换的循环节即可。
BEB(E[@S%7D5W3DPU3S.jpg)