最小生成树 - Prim
简介
什么是最小生成树?假设有 N 个点,通过 N - 1 条边将它们相连接,就叫做生成树,而最小就是这 N - 1 条边的权重相加最小,综合起来就是最小生成树。
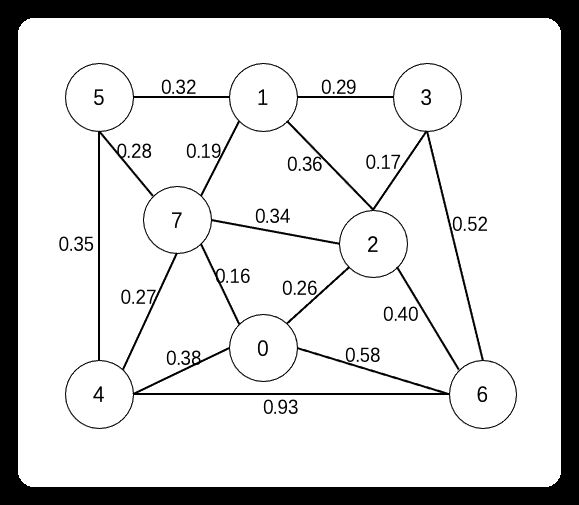
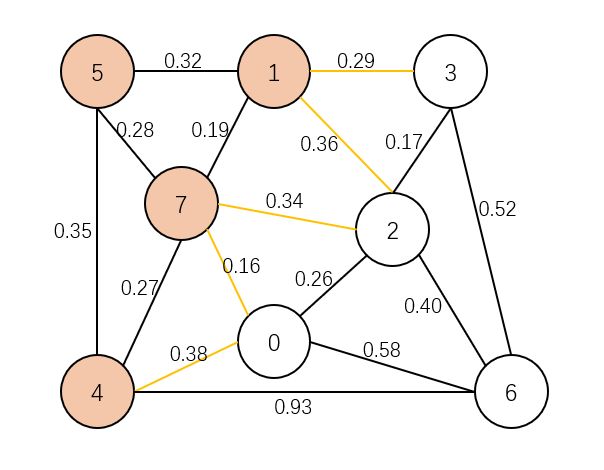
下面一张图:
按照最小生成树的规则,最终可以找到这样一条线:
0-7、7-5、5-4、7-1、0-2、2-3、2-6 7 条边把所有的点进行相连,形成了这张图的最小生成树。在这里也能看出来,想要找最小生成树,这个图必须是一个连通图,也就是没有其他的连通分量。
切分定理(Cut Property)
那通过什么样的方式可以求得总共有哪些边可以组成最小生成树?要想解决这个问题,就需要先了解一下什么是切分定理。
切分
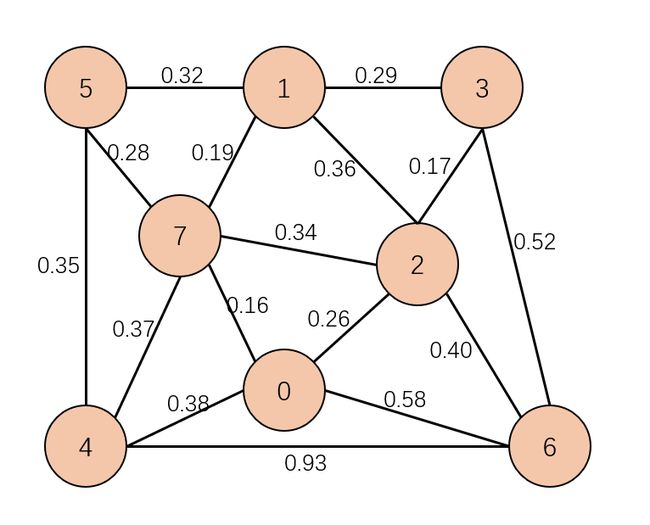
把一张图分成两部分就叫做切分,如下:
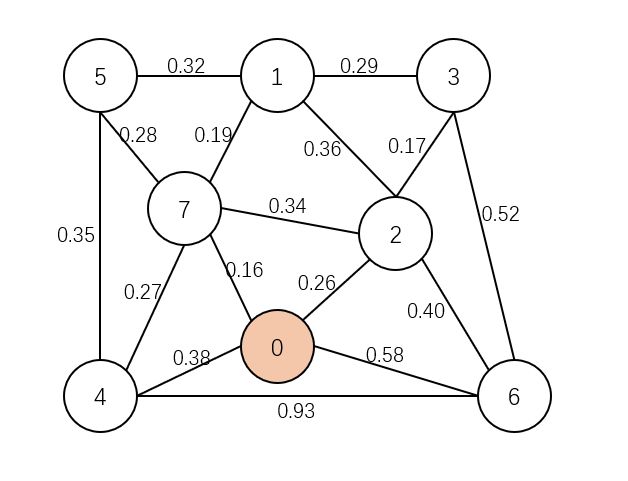
- 0 点为一部分
- 1、2、3、4、5、6、7 点为一部分
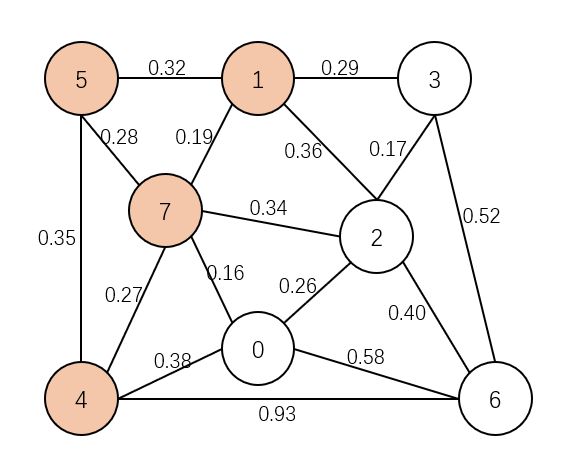
- 0、2、3、6 点为一部分
- 1、4、5、7 点为一部分
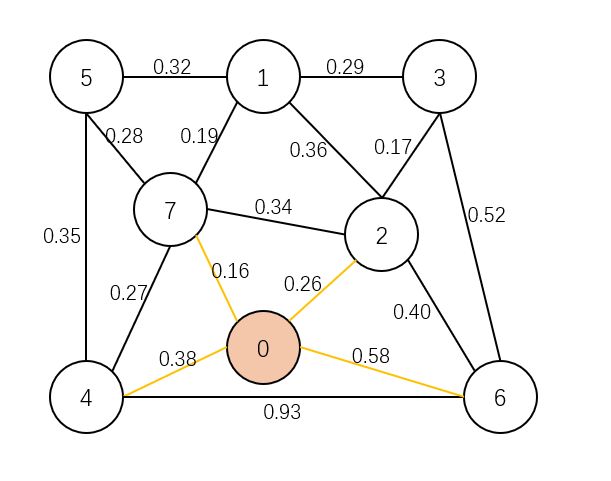
横切边
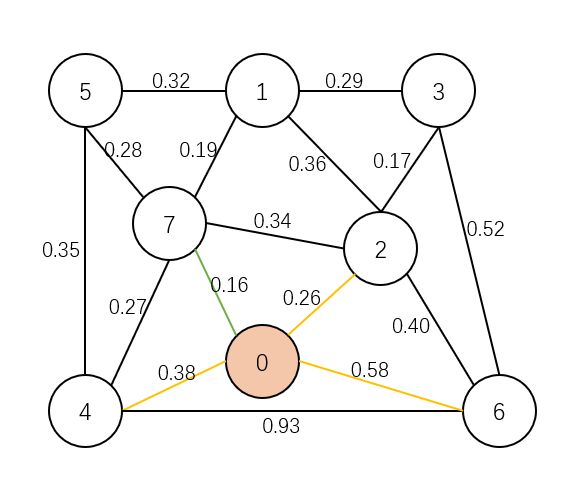
把一张图分成两部分之后,连接两部分中间的边叫做横切边,也可以理解为这条边连接的两个点分属这张图的不同部分。如下图:
切分定理
在了解了什么是切分、横切边之后,就可以进一步理解切分定理。切分定理定义为:给定任意切分,横切边中权值最小的边必然属于最小生成树。
Prim
Lazy Prim
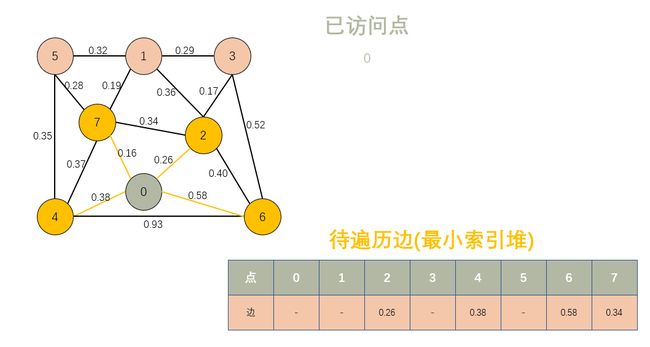
根据切分定理,将已访问过的点和未访问过的点做切分。
- 首先选定一个点进行访问,就从 0 开始。
- 把 0 标记为已访问。
- 遍历 0 的边,边另一头的点如果已经访问过,那就不是横切边,直接跳过,如果没访问过,那这条边就构成了横切边,把其放入最小堆中,方便下一步取最小的一条边。
- 从最小堆中取最小的边,保险起见,判断边两边的点访问状态(已访问或者未访问)是否一样,如果一样,大概率是都访问过了,直接跳过。
- 如果不一样,说明这条边肯定是横切边,而且还是最小的一条横切边,可以直接存储起来,其肯定是最小生成树中的一员。
- 判断 5 中得到的这条边的两个点,哪个还没访问过,就按照 2、3 条操作。
- 循环执行 4,如果堆中没数据了,就结束了。
动画演示
代码实现
#include
#include "MinHeap.h"
#include "../help/Edge.h"
/**
* 最小生成树
*
* Lazy Prim
*/
template
class LazyPrimMST {
private:
/** 图 */
Graph &G;
/** 最小堆数据结构,辅助获取最小边 */
MinHeap> pq;
/** 标记点是否被访问过 */
bool *marked;
/** 记录最小生成树包含的所有边 */
std::vector> mst;
/** 最小生成树的权值和 */
Weight mstWeight;
/**
* 访问点 v
*
* 把点 v 设置已访问过
* 遍历点 v 的边
* 边的另一头的点如果访问过了,就跳过。否则就加入最小堆。
*
* @param v
*/
void visit(int v) {
// 确定没访问过
assert(!marked[v]);
std::cout << "访问: " << v << std::endl;
// 把点 v 设置已访问过
marked[v] = true;
// 遍历点 v 的边
typename Graph::AdjIterator adjIter(G, v);
for (Edge *e = adjIter.begin(); !adjIter.end(); e = adjIter.next()) {
// 查看 边的另一头的点如果访问过了
if (!marked[e->other(v)]) {
// 没有访问过
pq.insert(*e);
}
}
}
public:
/**
* 初始化赋值图
*
* 最小堆的元素个数就是图边的总数
*/
LazyPrimMST(Graph &graph) : G(graph), pq(MinHeap>(graph.e())) {
// 初始化
marked = new bool[G.v()];
for (int i = 0; i < G.v(); ++i) {
marked[i] = false;
}
mst.clear();
// Lazy Prim 开始
// 先访问一下 0 索引位置
visit(0);
while (!pq.isEmpty()) {
// 只要待遍历的边不为空,就一直遍历。
// 取出最小的边
Edge e = pq.extractMin();
// 假如这个边的两点都已经被访问过,那就不是横切边了,跳过即可
if (marked[e.v()] == marked[e.w()]) {
continue;
}
// 既然是横切边并且还是最小权重,那肯定是最终的最小生成树的一条边,添加
mst.push_back(e);
// 继续访问下一个没有被访问过的点
if (!marked[e.v()]) {
visit(e.v());
} else {
visit(e.w());
}
}
mstWeight = mst[0].wt();
for (int i = 1; i < mst.size(); ++i) {
mstWeight += mst[i].wt();
}
}
~LazyPrimMST() {
delete[] marked;
}
/**
* 返回最小生成树的所有边
*/
std::vector> mstEdges() {
return mst;
};
/**
* 返回最小生成树的权值
*/
Weight result() {
return mstWeight;
};
};
测试
// testG1.txt
8 16
4 5 .35
4 7 .37
5 7 .28
0 7 .16
1 5 .32
0 4 .38
2 3 .17
1 7 .19
0 2 .26
1 2 .36
1 3 .29
2 7 .34
6 2 .40
3 6 .52
6 0 .58
6 4 .93
void testLazyPrim() {
string filename = "testG1.txt";
int v = 8;
SparseGraph g = SparseGraph(v, false);
ReadGraph, double> readGraph(g, filename);
// Test Lazy Prim MST
cout << "Test Lazy Prim MST:" << endl;
LazyPrimMST, double> lazyPrimMst(g);
vector> mst = lazyPrimMst.mstEdges();
for (int i = 0; i < mst.size(); i++)
cout << mst[i] << endl;
cout << "The MST weight is: " << lazyPrimMst.result() << endl;
cout << endl;
}
show:
Test Lazy Prim MST:
访问: 0
访问: 7
访问: 1
访问: 2
访问: 3
访问: 5
访问: 4
访问: 6
0-7: 0.16
7-1: 0.19
0-2: 0.26
2-3: 0.17
7-5: 0.28
5-4: 0.35
2-6: 0.4
The MST weight is: 1.81
Prim
经过上面的 Lazy Prim 的动画能看出来,整个过程中存在了不少一条边,其相连的两点都已经访问过,丢弃遍历的情况,这会增加对无用边的遍历次数,增大开销。Prim 就是来解决这个问题,在访问点的过程中,把无效的过滤掉。
-
首先选定一个点进行访问,就从 0 开始。
-
把 0 标记为已访问。
-
遍历 0 的边,边另一头的点如果已经访问过,那就不是横切边,直接跳过,如果没访问过,那这条边就构成了横切边。
-
把 0 到边另一头的点权重记录。
- 从索引堆中获取获取最小的权重,其必然是最小生成树的一员。此时获取的是
0.16。开始访问 7。 - 7 有 5 条边,0 是已经访问过的点,跳过,其他几点: 2、1、5、4,2 和 4 皆已存在记录,
7-2的权重为0.34,比已记录的0.26更大,舍弃,7-4的权重为0.37,比已记录的0.38小,更新已记录的值为0.37,其他两个 1、5 都还没记录,直接添加进去。 - 从索引堆中获取获取最小的权重,一直循环到取完为止。
动画演示
代码实现
#include
#include "IndexMinHeap.h"
#include "../help/Edge.h"
/**
* 最小生成树
*
* Prim
*
* 时间复杂度:O(ElogV)
*/
template
class PrimMST {
private:
/** 图 */
Graph &G;
/**
* 最小索引堆数据结构
* 用来存储“到达某些点的权重,一个点只会有一个权重,如果有更小的会修改掉”
*/
IndexMinHeap ipq;
/**
* 用来记录到已探索点的边,如果后续还不存在,就直接添加,已存在,更小的话就修改。
*/
vector *> edgeTo;
/** 标记点是否被访问过 */
bool *marked;
/** 记录最小生成树包含的所有边 */
std::vector> mst;
/** 最小生成树的权值和 */
Weight mstWeight;
/**
* 访问点 v
*
* 把点 v 设置已访问过
* 遍历点 v 的边
* 边的另一头的点如果访问过了,就跳过。否则就加入最小堆。
*
* @param v
*/
void visit(int v) {
// 确定没访问过
assert(!marked[v]);
std::cout << "访问: " << v << std::endl;
// 把点 v 设置已访问过
marked[v] = true;
// 遍历点 v 的边
typename Graph::AdjIterator adjIter(G, v);
for (Edge *e = adjIter.begin(); !adjIter.end(); e = adjIter.next()) {
// 取边(v-w)中的 w
int w = e->other(v);
// 查看 边的另一头的点如果访问过了
if (!marked[w]) {
// 没有访问过此点
if (!edgeTo[w]) {
// 也没有记录过到达此点的边
ipq.insert(w, e->wt());
edgeTo[w] = e;
} else if (e->wt() < edgeTo[w]->wt()) {
ipq.change(w, e->wt());
edgeTo[w] = e;
}
}
}
}
public:
/**
* 初始化赋值图
*
* 最小堆的元素个数就是图边的总数
*/
PrimMST(Graph &graph) : G(graph), ipq(IndexMinHeap(graph.v())) {
// 初始化
marked = new bool[G.v()];
for (int i = 0; i < G.v(); ++i) {
marked[i] = false;
edgeTo.push_back(nullptr);
}
mst.clear();
// Prim 开始
// 先访问一下 0 索引位置
visit(0);
while (!ipq.isEmpty()) {
// 只要待遍历的边不为空,就一直遍历。
// 取出最小的边的索引
int v = ipq.extractMinIndex();
mst.push_back(*edgeTo[v]);
visit(v);
}
mstWeight = mst[0].wt();
for (int i = 1; i < mst.size(); i++) {
mstWeight += mst[i].wt();
}
}
~PrimMST() {
delete[] marked;
}
/**
* 返回最小生成树的所有边
*/
std::vector> mstEdges() {
return mst;
};
/**
* 返回最小生成树的权值
*/
Weight result() {
return mstWeight;
};
};
测试
// testG1.txt
8 16
4 5 .35
4 7 .37
5 7 .28
0 7 .16
1 5 .32
0 4 .38
2 3 .17
1 7 .19
0 2 .26
1 2 .36
1 3 .29
2 7 .34
6 2 .40
3 6 .52
6 0 .58
6 4 .93
void testPrim() {
string filename = "testG1.txt";
int v = 8;
SparseGraph g = SparseGraph(v, false);
ReadGraph, double> readGraph(g, filename);
// Test Prim MST
cout<<"Test Prim MST:"<, double> primMST(g);
vector> mst = primMST.mstEdges();
for( int i = 0 ; i < mst.size() ; i ++ )
cout<
show:
Test Prim MST:
访问: 0
访问: 7
访问: 1
访问: 2
访问: 3
访问: 5
访问: 4
访问: 6
0-7: 0.16
7-1: 0.19
0-2: 0.26
2-3: 0.17
7-5: 0.28
5-4: 0.35
2-6: 0.4
The MST weight is: 1.81