DiffIR: Efficient Diffusion Model for lmage Restoration

DiffIR:用于图像复原的有效扩散模型

论文链接：https://arxiv.org/abs/2303.09472

项目链接：https://github.com/Zj-BinXia/DiffIR

Abstract

扩散模型(DM)通过将图像合成过程建模为去噪网络的顺序应用，实现了SOTA的性能。然而，与图像合成从头生成每个像素不同，图像复原(IR)的大部分像素是给定的。因此，对于IR，传统的DMs在大型模型上运行大量迭代来估计整个图像或特征映射是低效的。为了解决这个问题，我们提出了一种高效的IRDM (DiffIR)，它由紧凑的IR先验提取网络(CPEN)、动态IRtransformer(DIRformer)和去噪网络组成。具体来说，DiffIR有两个训练阶段：预训练和训练DM。在预训练中，我们将真实图像输入到CPEN_S1中，以捕获紧凑的IR先验表示(IPR)来指导DIRformer。在第二阶段，我们只使用LQ图像训练DM直接估计与预训练的CPEN_S1相同的IRP。我们观察到，由于IPR只是一个紧凑向量，DiffIR可以使用比传统DM更少的迭代来获得准确的估计，并产生更稳定和真实的结果。由于迭代次数少，我们的DiffIR可以采用CPEN_S2、diformer和去噪网络的联合优化，进一步降低了估计误差的影响。我们在几个IR任务上进行了广泛的实验，并在消耗更少的计算成本的同时实现了SOTA性能。

1. Introduction

由于图像复原具有广泛的应用价值和病态性，它一直是一个长期存在的问题。IR的目的是复原高质量(HQ)的图像从其低质量(LQ)对应损坏的各种退化因素(例如，模糊，蒙版，降采样)。目前，基于深度学习的IR方法已经取得了令人印象深刻的成功，因为它们可以从大规模数据集中学习强先验。

最近，扩散模型(Diffusion Models, DM)[49]是由去噪自编码器层次构建的，在图像合成[21,50,10,22]和IR任务(如inpainting[37,45]和超分辨率[47])中取得了令人印象深刻的结果。具体来说，训练DM通过反向扩散过程来迭代地去噪图像。DM已经表明，原则概率扩散建模可以实现从随机抽样的高斯噪声到复杂目标分布(如真实图像或潜在分布[45])的高质量映射，而不会像GAN那样遭受模型失效和训练不稳定性。

作为一类基于似然的模型，DM需要对大型去噪模型进行大量的迭代步骤(约50 ~ 1000步)来模拟数据的精确细节，这需要消耗大量的计算资源。与从头开始生成每个像素的图像合成任务不同，IR任务只需要在给定的LQ图像上添加精确的细节。因此，如果DM采用IR图像合成的范式，不仅会浪费大量的计算资源，而且容易产生一些与给定LQ图像不匹配的细节。

本文旨在设计一个基于DM的IR网络，充分有效地利用DM强大的分布映射能力来复原图像。为此，我们提出DiffIR。由于transformer可以模拟远程像素依赖关系，我们采用transformer块作为DiffIR的基本单元。我们将transformer块以Unet的形式堆叠形成动态transformer(Dynamic IRformer，简称DIRformer)来提取和聚合多层次特征。我们分两个阶段训练DiffIR：

(1) 在第一阶段(图2 (a))，我们开发了一个紧凑的IR先验提取网络(CPEN)，从真实图像中提取紧凑的IR先验表示(IPR)，以指导DIRformer。此外，我们还开发了动态门控前馈网络(DGFN)和动态多头转置注意(DMTA)，以充分利用IPR。值得注意的是，CPEN和DIRformer是一起优化的。

(2) 在第二阶段(图2 (b))，我们训练DM直接从LQ图像中估计准确的IPR。由于IPR较轻，仅添加细节进行复原，因此我们的DM可以估算出相当准确的IPR，并经过多次迭代获得稳定的视觉结果。

除了上述方案和架构的新颖性外，我们还展示了联合优化的有效性。在第二阶段，我们观察到估计的IPR可能仍然存在较小的误差，这将影响到DIRformer的性能。然而，以前的DM需要多次迭代，这对于将解码器一起优化DM是不可用的。由于我们的DiffIR需要很少的迭代，我们可以运行所有的迭代，得到估计的IDR，并与DIRformer联合优化。如图1所示，我们的DiffIR实现了SOTA性能，比其他基于DM的方法(例如RePaint[37]和LDM[45])消耗的计算量要少得多。特别是，DiffIR比RePaint效率高1000倍。我们的主要贡献有三个方面：

1. 我们提出了DiffIR，一个强大，简单，高效的基于DMIR基线。与图像合成不同，IR输入图像的大部分像素是给定的。因此，我们利用DM强大的映射能力来估计一个紧凑的IPR来指导IR，从而提高DM在IR中的复原效率和稳定性。
2. 我们提出DGTA和DGFN用于动态IRformer，以充分利用PIR。与以往单独优化去噪网络的潜在DM不同，我们提出了去噪网络和解码器(即DIRformer)的联合优化，以进一步提高估计误差的鲁棒性。
3. 大量实验表明，与其他基于DM的方法相比，所提出的DiffIR可以在IR任务中实现SOTA性能，同时消耗的计算资源要少得多。

2. Related Work

图像复原。作为先驱工作，SRCNN[13]、DnCNN[79]和ARCNN[12]采用紧凑型CNN在IR上取得了令人印象深刻的性能。此后，与传统IR方法相比，基于CNN的方法更受欢迎。到目前为止，研究人员已经从不同的角度对CNN进行了研究，得到了更精细的网络架构设计和学习方案，如残差块[27,76,6]、GAN[19,60,44]、注意力[81,61,9,67,66,63,68]、知识蒸馏[62]等[24,17,28,16,71]。

近年来，自然语言处理模型transformer在计算机视觉界获得了广泛的关注。与CNN相比，transformer可以模拟不同区域之间的全局相互作用，并达到最先进的性能。目前，transformer已被广泛应用于图像识别[15,55]、图像分割[57,64,82]、目标检测[5,84]、图像复原[7,35,69,33]等视觉任务中。

扩散模型。扩散模型(Diffusion Models, DM)[21]已经在密度估计[29]和样本质量[10]方面取得了最先进的结果。DM采用参数化马尔可夫链对似然函数的下变分界进行优化，使其生成的目标分布比GAN等生成模型更精确。近年来，DM在图像复原任务领域的影响力越来越大，如超分辨率[26,47]和图像修复[37,45]。SR3[47]将DM引入到图像超分辨率中，取得了比基于SOTA GAN的方法更好的性能。此外，Palette[46]受到条件生成模型[40]的启发，提出了IR的条件扩散模型。LDM[45]提出对潜空间进行DM以提高复原效率。此外，RePaint[37]通过DM中的重采样迭代设计了一种改进的去噪策略。然而，这些基于DM的IR方法直接使用DM的范式进行图像合成。然而，IR中的大部分像素是给定的，有必要对整个图像或特征图执行DM。我们的DiffIR在紧凑的IPR上执行DM，这可以使DM过程更加高效和稳定。

3. Preliminaries: Diffusion Models

在本文中，我们采用扩散模型(diffusion models, DM)[21]来生成准确的IR先验表示(IPR)。在训练阶段，DM方法定义了一个扩散过程，将输入图像$x_0$转换为高斯噪声$x_T\sim \mathcal{N}(0;1)$通过T次迭代。扩散过程的每次迭代可以描述如下:
$$q\left(x_t\mid x_{t-1}\right)=\mathcal{N}\left(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathbf{I}\right),\text{\hspace{1em}(1)}$$
式中，$x_t$为时间步长为$t$的噪声图像，${\beta }_t$为预定义的比例因子，$\mathcal{N}$为高斯分布。(1)式可进一步简化为：
$$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,\left(1-{\bar{\alpha }}_t\right)\mathbf{I}\right),\text{\hspace{1em}(2)}$$
其中${\alpha }_t=1-{\beta }_t,{\bar{\alpha }}_t={\prod }_{i=0}^t{\alpha }_i$。

在推理阶段(反向过程)，DM方法对高斯随机噪声图$x_T$进行采样，然后逐步对$x_T$进行降噪，直到得到高质量的输出$x_0$：
$$p\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)=\mathcal{N}\left({\mathbf{x}}_{t-1};{\mu }_t\left({\mathbf{x}}_t,{\mathbf{x}}_0\right),{\sigma }_t^2\mathbf{I}\right),\text{\hspace{1em}(3)}$$
其中均值${\mu }_t\left({\mathbf{x}}_t,{\mathbf{x}}_0\right)=\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-ϵ\frac{1-{\alpha }_t}{\sqrt{1-{\tilde{\alpha }}_t}}\right)$和方差${\sigma }_t^2=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}{\beta }_t$。$ϵ$表示$x_t$中的噪声，它是反向过程中唯一的不确定变量。DM采用去噪网络${ϵ}_{\theta }(x_t;T)$估计$ϵ$。训练${ϵ}_{\theta }(x_t;T)$，给定一个干净的图像$x_0$, DM随机采样时间步长$t$和噪声$ϵ\sim \mathcal{N}(0,\mathbf{I})$根据公式(2)生成带噪图像$x_t$。然后，DM对${ϵ}_{\theta }$的网络参数θ进行如下优化[21]：
∇ θ ∥ ϵ − ϵ θ ( α ˉ t x 0 + ϵ 1 − α ˉ t , t ) ∥ 2 2 . (4) \nabla_{\theta}\left\|\epsilon-\epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\mathrm{x}_{0}+\epsilon\sqrt{1-\bar{\alpha}_{t}},t\right)\right\|_{2}^{2}. \tag{4} ∇θ​ ​ϵ−ϵθ​(αˉt​ ​x0​+ϵ1−αˉt​ ​,t) ​22​.(4)

4. Methodology

传统的DM[49,45,37]需要大量的迭代、计算资源和模型参数来生成准确逼真的图像或潜在特征图。尽管DM在从头生成图像(图像合成)方面取得了令人印象深刻的性能，但将图像合成的DM范例直接应用于IR是浪费计算资源。由于IR中的大部分像素和信息都是给定的，因此对整幅图像或特征图进行DM不仅需要大量的迭代和计算，而且容易产生更多的伪影。总体而言，DM具有较强的数据估计能力，但将现有的DM模式应用到IR图像合成中效率不高。为了解决这一问题，我们提出了一种有效的IR分解模型(即DiffIR)，它采用分解模型估计一个紧凑的IPR来指导网络复原图像。由于IPR相当轻，因此与传统DM相比，DiffIR的模型尺寸和迭代可以大大减少，从而产生更准确的估计。

在本节中，我们将介绍DiffIR。如图2所示，DiffIR主要由紧凑的IR先验提取网络(CPEN)、动态IR transformer(DIRformer)和去噪网络组成。我们分两个阶段训练DiffIR，包括DiffIR的预训练和扩散模型的训练。在接下来的章节中，我们首先介绍4.1节中的预训练DiffIR。然后，我们在4.2节中提供了DiffIR的训练效率DM的细节。

4.1. Pretrain DiffIR

在介绍预训练DiffIR之前，我们想在第一阶段介绍两个网络，包括紧凑型IR先验提取网络(CPEN)和动态IRformer (DIRformer)。CPEN的结构如图2黄色方框所示，主要由残差块和线性层堆叠，以提取紧凑的IR先验表示（IPR）。之后，DIRformer可以使用提取的IDR来复原LQ图像。DIRformer的结构如图2粉色方框所示，由Unet形状的动态DIRformer块堆叠而成。动态DIRformertransformer模块由动态多磁头转置注意(DMTA，图2绿框)和动态门控前馈网络(DGFN，图2蓝框)组成，可以使用IDR作为动态调制参数，将复原细节添加到特征图中。

在预训练中(图2 (a))，我们将CPEN_S1和DIRformer一起训练。具体来说，我们首先将ground-truth和LQ图像连接在一起，并使用PixelUnshuffle操作对它们进行下采样，以获得CPEN_S1的输入。然后，CPEN_S1提取IPR $\mathbf{Z}\in {\mathbb{R}}^{4C^{\prime }}$为：
$$\mathbf{Z}={\mathrm{CPEN}}_{\mathrm{S}1}(\mathrm{PixelUnshuffle}(\mathrm{Concat}(I_{GT},I_{LQ}))).\text{\hspace{1em}(5)}$$
然后将IPR Z作为动态调制参数送入DIRformer的DGFN和DMTA，指导复原：
$${\mathbf{F}}^{\prime }=W_l^1\mathbf{Z}\odot \mathrm{Norm}(\mathbf{F})+W_l^2\mathbf{Z},\text{\hspace{1em}(6)}$$
式中$\odot$表示逐元素乘法，Norm表示层归一化[2]，$W_l$表示线性层，$\mathbf{F}$和${\mathbf{F}}^{\prime }\in {\mathbb{R}}^{\hat{H}\times \hat{W}\times \hat{C}}$分别为输入和输出特征映射，$W_l^1\mathbf{Z},W_l^2\mathbf{Z}\in {\mathbb{R}}^C$。

然后，我们在DMTA中聚合了全局空间信息。具体来说，${\mathbf{F}}^{\prime }$被投影为查询$\mathbf{Q}=W_d^Q{W}_c^Q{\mathbf{F}}^{\prime }$，键$\mathbf{K}=W_d^K{W}_c^K{\mathbf{F}}^{\prime }$，值$\mathbf{V}=W_d^V{W}_c^V{\mathbf{F}}^{\prime }$，其中$W_c$为$1\times 1$点卷积，$W_d$为$3\times 3$深度卷积。接下来，我们重塑查询，$\hat{\mathbf{Q}}\in {\mathbb{R}}^{\hat{A}\hat{W}\times \hat{C}}$，键$\hat{\mathbf{K}}\in {\mathbb{R}}^{\widehat{C\times }\hat{H}}$和值$\hat{\mathbf{V}}\in {\mathbb{R}}^{\hat{H}\hat{W}\times \hat{C}}$。之后，我们在$\hat{\mathbf{Q}}$和$\hat{\mathbf{K}}$之间进行点积，生成大小为的${\mathbb{R}}^{C\times C}$转置注意图$\mathbf{A}$，它比大小为${\mathbb{R}}^{\hat{H}\hat{W}\times \hat{H}\hat{W}}$的常规注意图更有效。DMTA的整个过程可以描述如下：

$$\hat{\mathbf{F}}=W_c\hat{\mathbf{V}}\cdot \mathrm{Softmax}(\hat{\mathbf{K}}\cdot \hat{\mathbf{Q}}/\gamma )+\mathbf{F},\text{\hspace{1em}(7)}$$
其中$\gamma$是可学习的缩放参数。与传统的多头自注意一样[15,7]，我们将通道划分为多头并计算注意图。

接下来，在DGFN中，我们聚合局部特征。我们使用1×1卷积对不同通道的信息进行聚合，采用3 × 3深度卷积对空间相邻像素的信息进行聚合。此外，我们还采用了门控机制来增强信息编码。DGFN的整个过程定义为：
$$\hat{\mathbf{F}}=\mathrm{GELU}\left(W_d^1{W}_c^1{\mathbf{F}}^{\prime }\right)\odot W_d^2{W}_c^2{\mathbf{F}}^{\prime }+\mathbf{F}.\text{\hspace{1em}(8)}$$
我们将CPEN_S1和DIRformer一起训练，使DIRformer能够充分利用CPEN_S1提取的IPR进行复原。训练损失定义如下：
L r e c = ∥ I G T − I ^ H Q ∥ 1 , (9) L_{rec}=\left\|I_{GT}-\hat{I}_{HQ}\right\|_{1}, \tag{9} Lrec​= ​IGT​−I^HQ​ ​1​,(9)
其中$I_{GT}$和${\hat{I}}_{HQ}$分别是ground-truth和复原的HQ图像。$\Vert \cdot {\Vert }_1$表示L1范数。如果有些工作强调视觉质量，如inpainting和SISR，我们可以进一步增加感性损失和对抗性损失。在补充材料中提供了更多的细节。

4.2. 图像复原的扩散模型

在第二阶段(图2 (b))，我们利用DM强大的数据估计能力来估计IPR。具体来说，我们使用预训练的CPEN_S1来捕获IPR $\mathbf{Z}\in {\mathbb{R}}^{4C^{\prime }}$。之后，我们将Z上的扩散过程应用到采样${\mathbf{Z}}_T\in {\mathbb{R}}^{4C^{\prime }}$上，可以描述为：
$$q\left({\mathbf{Z}}_T\mid \mathbf{Z}\right)=\mathcal{N}\left({\mathbf{Z}}_T;\sqrt{{\bar{\alpha }}_T}\mathbf{Z},\left(1-{\bar{\alpha }}_T\right)\mathbf{I}\right),\text{\hspace{1em}(10)}$$
其中T是迭代的总次数，$\bar{\alpha }$和$\alpha$在公式(1)和(2)中定义。(即${\bar{\alpha }}_T={\prod }_{i=0}^T{\alpha }_i$)。

在反向的过程中，由于IPR是紧凑的，DiffIR_S2可以使用比传统DM更少的迭代和更小的模型尺寸来获得相当好的估计[45,37]。由于传统的DM在迭代中有巨大的计算成本，它们必须随机采样一个时间步$t\in [1,T]$，仅在该时间步长优化去噪网络(公式(1)、(2)、(3)、(4))由于去噪网络和解码器(即DIRformer)缺乏联合训练，意味着去噪网络引起的估计误差很小，使DIRformer无法发挥其潜力。相比之下，DiffIR从第t个时间步长(公式(10))开始，运行所有去噪迭代(公式(11))，得到$\hat{Z}$，并将其传递给DIRformer进行联合优化。
$${\hat{\mathbf{Z}}}_{t-1}=\frac{1}{\sqrt{{\alpha }_t}}\left({\hat{\mathbf{Z}}}_t-ϵ\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}\right),\text{\hspace{1em}(11)}$$
其中$ϵ$表示相同的噪声，我们使用CPEN_S2和去噪网络来预测公式(3)中的噪声。值得注意的是，与公式(3)中的传统DM不同，我们的DiffIR_S2删除了方差估计，并发现它有助于准确的IPR估计和更好的性能(第6节)。

在DM的反向过程中，我们首先使用CPEN_S2从LQ图像中获得条件向量$\mathbf{D}\in {\mathbb{R}}^{4C^{\prime }}$:
$$\mathbf{D}={\mathrm{CPEN}}_{\mathrm{S}2}(\mathrm{PixelUnshuffle}(I_{LQ})),\text{\hspace{1em}(12)}$$
其中，除了第一次卷积的输入维不同，CPEN_S2与CPEN_S1具有相同的结构。然后，我们使用去噪网络θ估计每个时间步t中的噪声为${ϵ}_{\theta }(\mathrm{Concat}({\hat{\mathbf{Z}}}_t,t,\mathbf{D})).$。将估计的噪声代入公式(11)，得到${\hat{Z}}_{t-1}$，开始下一次迭代。

然后，经过T次迭代，我们得到最终估计的IPR $\hat{\mathbf{Z}}\in {\mathbb{R}}^{4C^{\prime }}$。我们使用L_all联合训练DPEN_S2、去噪网络和DIRformer：
L d i f f = 1 4 C ′ ∑ i = 1 4 C ′ ∣ Z ^ ( i ) − Z ( i ) ∣ , L a l l = L r e c + L d i f f , (13) \begin{aligned}\mathcal{L}_{diff}=\frac{1}{4C'}\sum_{i=1}^{4C'}\left|\hat{\mathbf{Z}}(i)-\mathbf{Z}(i)\right|, \mathcal{L}_{all}=\mathcal{L}_{rec}+\mathcal{L}_{diff}, \end{aligned} \tag{13} Ldiff​=4C′1​i=1∑4C′​ ​Z^(i)−Z(i) ​,Lall​=Lrec​+Ldiff​,​(13)
我们可以在L_all中进一步添加感知损失和对抗损失，以获得更好的视觉质量，如公式(9)。

在推理阶段，我们只使用反向扩散过程(图2 (b)底部)。CPEN_S2从LQ图像中提取条件向量D，随机抽取高斯噪声${\hat{Z}}_T$。去噪网络利用${\hat{Z}}_T$和D来估计T次迭代后的IPR $\hat{Z}$。之后，DIRformer利用IPR复原LQ映像。

5. Experiments

5.1. 实验设置

我们将我们的方法分别应用于三种典型的IR任务:(a)图像修复，(b)图像超分辨率(SR)， ©单图像运动去模糊。我们的DiffIR采用4级编码器-解码器结构。从1级到4级，DMTA的注意头依次为[1,2,4,8]，通道数为[48,96,192,384]。此外，在所有IR任务中，我们调整了DIRformer中动态transformer块的数量，以比较DiffIR和SOTA方法在相似参数和计算成本方面的差异。具体来说，从第1层到第4层，我们设置动态transformer块数为[1,1,1,9]、[13,1,1,1],[3,5,6,6]分别用于图像修复、SR和去模糊。此外，根据之前的工作[37,45]，我们引入了针对图像修复和SR的对抗损失和感知损失。CPEN的通道数$C^{\prime }$设置为64。

在训练扩散模型时，将总时间步长T设为4，公式(11)中的βt (αt = 1−βt)从β1 = 0.1线性增加到βt = 0.99。我们使用Adam优化器(β1 = 0.9， β2 = 0.99)训练模型。更多的细节载于补充材料中。

5.2. 图像修复评估

我们使用LaMa的相同设置来训练和验证我们的DiffIRS2的inpainting[52]。具体来说，我们分别在Places-Standard[83]和CelebA-HQ[25]数据集上训练了batch大小为30和patch大小为256的DiffIR。我们使用LPIPS[80]和FID[20]在验证数据集上比较了DiffIRS2与SOTA的图像修复方法(ICT [56]， LaMa[52]和RePaint[37])。

定量结果如表1和图1 (a)所示。我们可以看到，我们的DiffIR_S2明显优于其他方法。具体来说，我们的DiffIR_S2超过竞争方法LaMa的FID裕度高达0.2706和0.5583，在Places和CelebA-HQ上具有宽掩模，消耗相似的参数和multiadd总数。此外，与基于DM的RePaint方法相比[45]，我们的DiffIR_S2在仅消耗4.3%的参数和0.1%的计算资源的情况下可以获得更好的性能。这表明DiffIR可以充分有效地利用DM对IR的数据估计能力。

定性结果如图3所示。我们的DiffIR_S2可以产生比其他竞争对手的图像补全方法更真实合理的结构和细节。在补充材料中提供了更多的定性结果。

5.3. 图像超分辨率评估

我们在图像超分辨率上训练和验证了DiffIR_S2。具体来说，我们在DIV2K[1] (800张图像)和Flickr2K[54] (2650张图像)数据集上训练DiffIR_S2，用于4倍超分辨率。批量大小设置为64,LQ补丁大小设置为64×64。我们使用LPIPS[80]和DISTS[11]在五个基准(Set5 [3]， Set14 [72]， General100 [14]， Urban100[23]和DIV2K100[1])上评估了我们的DiffIRS2和其他基于SOTA GAN的SR方法。

表2和图1 (b)显示了DiffIR_S2与基于SOTA GAN的SR方法SFTGAN[59]、SRGAN[32]、ESRGAN[60]、USRGAN[75]、SPSR[39]和BebyGAN[34]的性能和multiadd比较。我们可以看到DiffIR_S2达到了最好的性能。与竞争对手的SR方法BebyGAN相比，我们的DiffIR_S2在General100和Urban100上的LPIPS差值高达0.0121和0.0175，而仅消耗63%的计算资源。此外，值得注意的是，DiffIR_S2在消耗2%计算资源的情况下显著优于基于DM的方法LDM。

定性结果如图4所示。DiffIR_S2实现了最好的视觉质量，包含更多的现实细节。这些视觉对比与定量结果一致，显示了DiffIR的优越性。DiffIR可以有效地使用强大的DM来复原图像。补充材料中给出了更多的视觉结果。

5.4. 图像运动去模糊评估

我们在GoPro[41]数据集上训练DiffIR用于图像运动去模糊，并在两个经典基准(GoPro, HIDE[48])上评估DiffIR。我们将DiffIR_S2与最先进的图像运动去模糊方法进行了比较，包括Restormer[69]、MPRNet[70]和IPT[7]。

定量结果(PSNR和SSIM)如表3所示，Multi-Adds如图1 ©所示。我们可以看到，我们的DiffIR_S2优于其他运动去模糊方法。具体来说，DiffIR_S2在GoPro上分别比IPT和MIMIUnet+高0.68 dB和0.54 dB。此外，DiffIR_S2在GoPro和HIDE数据集上分别比Restormer高0.28 dB和0.33 dB，仅消耗78%的计算资源。这证明了DiffIR的有效性。

定性结果如图5所示，我们的DiffIR_S2具有最好的视觉质量，包含更接近相应HQ图像的逼真细节。在补充材料中提供了更多的定性结果。

6. Ablation Study

图像复原的有效扩散模型。在这一部分中，我们验证了DiffIR中DM、DM的训练方案以及是否在DM中插入方差噪声等成分的有效性(表4)。

(1) DiffIR_S2- v3实际为表1中采用的DiffIR_S2, DiffIR_S1为以真地图像为输入的第一阶段预训练网络。比较DiffIRS1和DiffIR_S2-V3，我们可以看到DiffIR_S2-V3的LPIPS与DiffIR_S1非常相似，这意味着DM具有强大的数据建模能力，可以准确预测IPR。

(2) 为了进一步证明DM的有效性，我们取消了在DiffIRS2-V3中使用DM来获得DiffIRS2V1。比较DiffIR_S2-V1和DiffIR_S2-V3，我们可以看到DiffIR_S2-V3(使用DM)明显优于DiffIR_S2-V1。这意味着DM学习到的IPR可以有效地指导DIRformer复原LQ图像。

(3) 为了探索更好的DM训练方案，我们比较了传统DM优化和我们提出的联合优化两种训练方案。由于传统的DM[45,49]需要多次迭代来估计大型图像或特征图，因此必须采用传统的DM优化，通过随机采样一个时间步来优化去噪网络，而后者无法使用后面的解码器(即本文中的DIRformer)进行优化。由于DiffIR仅使用DM来估计紧凑的一维向量IPR，因此我们可以使用多次迭代来获得相当准确的结果。因此，我们可以采用联合优化的方式，运行去噪网络的所有迭代，获得IPR并与DIRformer共同优化。比较DiffIR_S2-V2和DiffIR_S2-V3, DiffIR_S2-V3显著超过了DiffIR_S2-V2，这证明了我们提出的联合优化训练DM的有效性。这是因为DM在IPR中较小的估计误差可能导致DIRformer的性能下降。联合培训DM和DIRformer可以解决这个问题。

(4) 在传统的DM方法中，他们会在反向DM过程中插入方差噪声(公式(3))来生成更真实的图像。与传统的DM预测图像或特征图不同，我们使用DM来估计IPR。在DiffIR_S2-V4中，我们在反向DM过程中添加噪声。我们可以看到，DiffIR_S2-V3比DiffIR_S2-V4实现了更好的性能。这意味着为了保证估计的IPR的准确性，最好消除添加噪声。

DM的损失函数。我们探索哪种损失函数最适合指导去噪网络和CPEN_S2学习从LQ图像中估计准确的IPR。这里，我们定义了三个损失函数。(1)我们定义L_dif进行优化(公式(13))。(2)我们采用L₂ (公式(14))来度量估计误差。(3)我们使用Kullback Leibler散度来度量分布相似性(L_kl, 公式(15))。
$$\begin{array}{r}{\mathcal{L}}_2=\frac{1}{4C^{\prime }}\sum _{i=1}^{4C^{\prime }}{\left(\hat{\mathbf{Z}}(i)-\mathbf{Z}(i)\right)}^2,\\ {\mathcal{L}}_{kl}=\sum _{i=1}^{4C^{\prime }}{\mathbf{Z}}_{norm}(i)\log \left(\frac{{\mathbf{Z}}_{norm}(i)}{{\hat{\mathbf{Z}}}_{norm}(i)}\right),\end{array}\text{\hspace{1em}(14)(15)}$$
其中$\hat{\mathbf{Z}}$和$\mathbf{Z}\in {\mathbb{R}}^{4C^{\prime }}$分别为DiffIR_S1和DiffIR_S2提取的IPR。${\hat{\mathbf{Z}}}_{\text{norm }}$和${\mathbf{Z}}_{\text{norm }}\in {\mathbb{R}}^{4C^{\prime }}$分别用$\hat{\mathbf{Z}}$和$\mathbf{Z}$的softmax操作归一化。我们分别在DiffIR_S2上应用这三个损失函数，学习直接从LQ图像中估计准确的IPR。然后，我们在CelebA-HQ上对他们进行了评估。结果如表5所示。我们可以看到L_dif的性能优于L₂和L_kl。

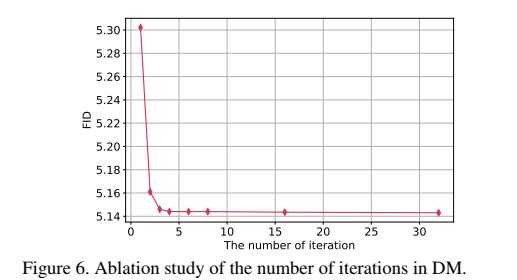
迭代次数的影响。在这一部分中，我们将探讨DM中的迭代次数如何影响DiffIR_S2的性能。我们在DiffIR_S2中设置了不同的迭代次数，并在公式(10)中调整βt（αt=1−βt），使Z在扩散过程（即${\bar{\alpha }}_T\to 0$）后成为高斯噪声$Z_T\sim \mathcal{N}(0,1)$。结果如图6所示。当迭代增加到3次时，DiffIR_S2的性能将显著提高。当迭代次数大于4次时，DiffIR_S2几乎保持稳定，即达到上界。此外，我们可以看到，我们的DiffIR_S2收敛速度比传统DM更快(需要200多次迭代)。这是因为我们仅仅对IPR(一个紧凑的一维向量)执行DM。

7. Conclusion

传统的DM在图像合成方面取得了令人印象深刻的性能。与从头开始生成每个像素的图像合成不同，IR给出了LQ图像作为参考。因此，将传统的决策模型直接应用于IR是低效的。在本文中，我们提出了一种有效的IR扩散模型(即DiffIR)，该模型由CPEN、Diformer和去噪网络组成。具体来说，我们首先将ground-truth 图像输入到CPEN_S1中，生成一个紧凑的IPR来指导DIRformer。然后，我们训练DM来估计CPEN_S1提取的IPR。与传统的DM相比，我们的DiffIR可以比传统的DM使用更少的迭代来获得准确的估计，并减少复原图像中的伪影。此外，由于迭代次数少，我们的DiffIR可以采用CPEN_S2、Diformer和去噪网络的联合优化，以减少估计误差的影响。大量实验表明，DiffIR可以达到一般的SOTA IR性能。

Appendix

A. Appendix

B. Evaluation on Real-world SR

C. Algorithm

D. More Training Details on Inpainting

E. More Training Details on SR

F. More Training Details on deblurring

G. More Visual Comparisons on Inpainting

H. More Visual Comparisons on SR

I. More Visual Comparisons on Deblurring