数据结构基础：P10.1-排序(二)---＞快速排序

本系列文章为浙江大学陈越、何钦铭数据结构学习笔记，前面的系列文章链接如下：
数据结构基础：P1-基本概念
数据结构基础：P2.1-线性结构—＞线性表
数据结构基础：P2.2-线性结构—＞堆栈
数据结构基础：P2.3-线性结构—＞队列
数据结构基础：P2.4-线性结构—＞应用实例：多项式加法运算
数据结构基础：P2.5-线性结构—＞应用实例：多项式乘法与加法运算-C实现
数据结构基础：P3.1-树(一)—＞树与树的表示
数据结构基础：P3.2-树(一)—＞二叉树及存储结构
数据结构基础：P3.3-树(一)—＞二叉树的遍历
数据结构基础：P3.4-树(一)—＞小白专场：树的同构-C语言实现
数据结构基础：P4.1-树(二)—＞二叉搜索树
数据结构基础：P4.2-树(二)—＞二叉平衡树
数据结构基础：P4.3-树(二)—＞小白专场：是否同一棵二叉搜索树-C实现
数据结构基础：P4.4-树(二)—＞线性结构之习题选讲：逆转链表
数据结构基础：P5.1-树(三)—＞堆
数据结构基础：P5.2-树(三)—＞哈夫曼树与哈夫曼编码
数据结构基础：P5.3-树(三)—＞集合及运算
数据结构基础：P5.4-树(三)—＞入门专场：堆中的路径
数据结构基础：P5.5-树(三)—＞入门专场：File Transfer
数据结构基础：P6.1-图(一)—＞什么是图
数据结构基础：P6.2-图(一)—＞图的遍历
数据结构基础：P6.3-图(一)—＞应用实例：拯救007
数据结构基础：P6.4-图(一)—＞应用实例：六度空间
数据结构基础：P6.5-图(一)—＞小白专场：如何建立图-C语言实现
数据结构基础：P7.1-图(二)—＞树之习题选讲：Tree Traversals Again
数据结构基础：P7.2-图(二)—＞树之习题选讲：Complete Binary Search Tree
数据结构基础：P7.3-图(二)—＞树之习题选讲：Huffman Codes
数据结构基础：P7.4-图(二)—＞最短路径问题
数据结构基础：P7.5-图(二)—＞哈利·波特的考试
数据结构基础：P8.1-图(三)—＞最小生成树问题
数据结构基础：P8.2-图(三)—＞拓扑排序
数据结构基础：P8.3-图(三)—＞图之习题选讲-旅游规划
数据结构基础：P9.1-排序(一)—＞简单排序(冒泡、插入)
数据结构基础：P9.2-排序(一)—＞希尔排序
数据结构基础：P9.3-排序(一)—＞堆排序
数据结构基础：P9.4-排序(一)—＞归并排序

---

一、算法概述

下面我们要讲的快速排序是传说中在现实应用中最快的一种排序算法。

其实上一次我们讲到过，没有任何一种排序算法是在任何情况下都是最好的，所以快速排序也不是在任何情况下都是最好的，我们总是可以构造出一种他的最坏情况。在最坏的情况下，快速排序算法的表现也可能是非常糟糕，但是在大多数的情况下，对于大规模的随机数据，快速排序的表现还是相当出色的。但是，前提条件是你把快速排序中所有的小细节都实现的非常到位。因为快速排序的一个特点就是你自己写的话很容易写错，一不小心有一个细节实现的不好他就不是快速排序了，他还会相当的慢。

快速排序的算法跟规并函数的算法有一定的相似之处，就在于他们的策略都是采用的分而治之的策略。一说分而治之我们马上就想到了递归，差不多就是这个意思。我们来看一个例子：

比如说我们给了一堆的整数

快速排序的第一步就是从这堆整数里面随便挑一个元素出来做主元，比如说我选中了65来做这个主元(pivot)

以65为枢纽，把我们原来的数字集合就分成了两大块：左边的这一块包含的所有的数字都小于65，右边集合包括的数字全部都大于65，这就是分的过程

然后我们递归地去治左边和右边，最后治理完成后的结果如下所示

最后把这三块放在一个数组里就完成了快速排序

对应伪代码描述如下：

void Quicksort( ElementType A[], int N ) 
{ 
	if ( N < 2 ) return;
	pivot = 从A[]中选一个主元; 
	将S = { A[] \ pivot } 分成2个独立子集:
		A1={ a属于S | a <= pivot } 和
		A2={ a属于S | a <= pivot };
	A[] = Quicksort(A1,N1)并{pivot}并Quicksort(A2,N2);
}

上面代码中有很多的细节要注意：

1、第一个就是主元要怎么选。主元选的不好的话，你的快速排序一点都不快，他会变得非常慢。
2、第二个就是根据这个主元把它分成两个独立子集。说起来容易，怎么分呢？这个分的过程如果耗费的时间太多，快速排序也快不起来。

二、选主元

方法1：直接取A[0]
一个非常简单直截了当的想法就是直接把pivot取成A[0]。这其实是一种非常不聪明的取法，我们举个例子：

我们的初始序列一开始就长成这样

他一开始就是有序的，这个时候快速排序先选了A[0]作为主元

选了A[0]作为主元之后，他必须要把剩下的元素都扫描一遍，然后发现这个主元是最小的。于是在子集划分的时候，他就发现他的左边是空集，右边包含了N-1个元素。然后他就要对这N-1个元素进行递归的去处理。仍然选取第一个元素为主元。

然后继续递归划分

复杂度如下：

方法2：随机取
一种比较安全的方法就是随机取，但是随机你要涉及到一个随机函数rand()。这个随机函数要花的时间较多，故不考虑。

方法3：取头、中、尾的中位数
例如数列的头、中、尾元素分别是8、12、3，排序后就是3 8 12，中位数就是8。对应伪代码如下：

ElementType Median3( ElementType A[], int Left, int Right ) 
{ 
	int Center = ( Left + Right ) / 2; 
	if ( A[ Left ] > A[ Center ] )  //此时A[Left]
		Swap( &A[ Left ], &A[ Center ] ); 
	if ( A[ Left ] > A[ Right ] )  //此时A[Left]一定是最小的元素
		Swap( &A[ Left ], &A[ Right ] ); 
	if ( A[ Center ] > A[ Right ] )  //此时一定是A[Left]
		Swap( &A[ Center ], &A[ Right ] ); 
	/* A[ Left ] <= A[ Center ] <= A[ Right ] */ 
	Swap( &A[ Center ], &A[ Right-1 ] ); /* 将pivot藏到右边 */ 
	/* 只需要考虑 A[ Left+1 ] … A[ Right–2 ] */
	return A[ Right-1 ]; /* 返回 pivot */ 
}

三、子集划分

3.1 快速排序算法流程

例子：

现在我有10个数字，当然我们对着10个数字先调用了median3函数，找到了主元为6。

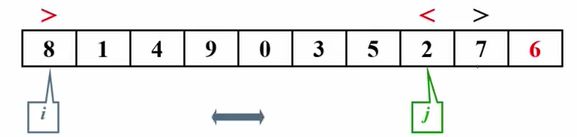
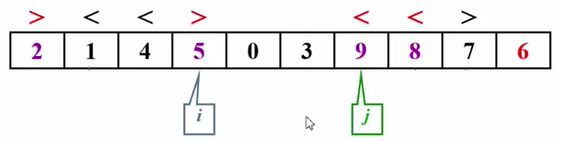
这个时候我要开始找6这个元素应该被放在哪里，将这10个数分成两个独立子集。那首先我们定一个左边的指针i，再定一个右边的指针j。

我们要做的第一件事情就是先比较i所指的这个元素跟我们的主元谁大谁小。那我发现8是大于6的，那我在这发出了一个红色警告，就说这个事情不对了，因为我们需要左边的元素全部都要小于等于6。

然后我去考虑j，7是大于6的，没问题。

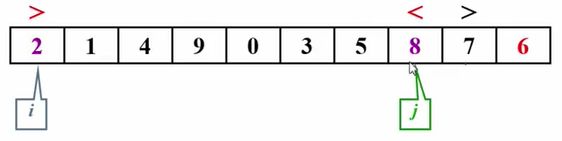
于是j--，往左边移动到2。然后发现2这个元素是小于6的，于是 红色警报又不对了。在两边都发现了有不对的元素以后，我们应该把这两个元素交换一下。

于是进行交换

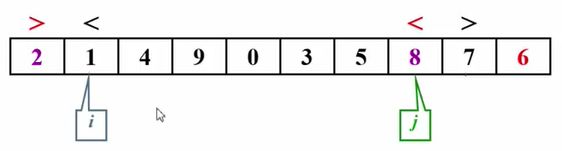
然后我们就开始下一轮的比较，i+1去指向下一个元素。这个时候我们发现1是小于6的，没有问题，然后继续i+1。

4也是小于6的 没有问题，需要继续i+1。

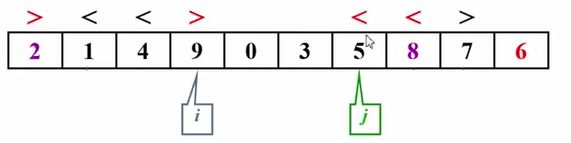
然后我们发现错了，9是大于6的，在这个地方停住。

然后转去考虑这个j。j-1，然后我们比较5和6，发现不对，这个5是小于6的，所以在这停住。

进行交换

i继续走，发现0<6，没问题

3小于6，没问题

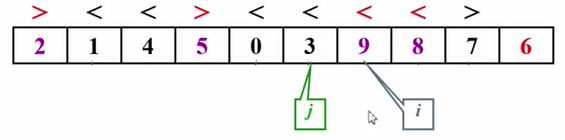
i继续走，此时9>6，不对，停住

j往前移动，3<6，不对了，停住

此时i越过j了，说明这次划分结束了。最后将主元6换到正确的地方，就是6在的地方。

3.2 算法分析

快速排序为什么快

快就在于每一次他选定一个主元以后，这个主元在子集划分完成以后，它就被一次性的放到了最终的正确位置上。它不像插入排序，每一次做了元素交换以后，这个元素所待的位置只是临时的，当下一张新的扑克牌插进来的时候，它会发现这些牌的位置全部都要往后错，所以一张牌可能在你插入排序的过程中被移动了很多次。快速排序之所以快的一个很重要的原因，就是他的主元被选中以后，在子集划分完成之后他被一次性的放到了正确的位置上，以后再也不会移动。

有一个很有趣的情况，我们必须要考虑一下：如果有元素正好等于这个主元，我们要怎么做？

①停下来交换
让我们来考虑一种非常极端的情况，也就是这个元素里面所有的元素都是相等的，比如说他们全部都是等于1的。那我们首先调用median3，比一比头、尾、中间，发现都不用动，于是把中间的元素换到了右边的位置。然后我就开始考虑两个指针，i和j。比较了一下，发现i和j对应元素相等且都等于主元，于是他们做了一个交换，然后i++、j--。
那我们就发现：当所有的元素都相等的时候，他会做很多很多很多次完全没有用处的交换。这个事情是不是有点傻呢？但是你不要忘了他有一个好处，就是做了很多无谓的交换以后，最后i和j会停在比较中间的位置。于是最后我们的主元会被换到中间的位置，那这么做的一个好处就是：每一次递归的时候，这个原始的序列都被基本上等分成两个等长的序列，也就是N/2的序列，然后往下递归。前面我们做过时间复杂度分析了，我们知道这样做的最后的时间复杂度应该是$O(NlogN)$。
②不理它，继续移动指针
如果碰到相等的元素，我不理他，继续移动我的指针。那么在刚才那种全部元素都相等的条件下，我在开始做子集划分的时候，我要先从左边的i开始，然后发现i这个元素等于主元，他就不理他，然后继续往前一直移动。它会一直移动到右端，直到他碰到了j，那么j其实根本都没有机会移动。这样的好处是我避免了很多没有用的交换，但是他的坏处也很明显：每一次子集划分的时候，基本上你的主元都是被放在某一个端点的，于是我们就回到了前面最囧的那个状态，也就是变成了一个$O(N^2)$复杂度的算法

快速排序的问题

用递归
递归会占用额外的系统堆栈的空间，而且每一次调用系统堆栈的时候，会有很多的进栈，然后一次递归结束以后，返回时要pop很多东西。所以整个递归的过程其实是很慢的，对小规模的数据(例如N不到100)可能还不如插入排序快
解决方案
在程序中定义一个Cutoff阈值，当递归的数据规模充分小，则停止递归，直接调用简单排序(例如插入排序)。

四、算法实现

对应代码如下：

void Quicksort( ElementType A[], int Left, int Right ) 
{ 
//>=阈值，使用快速排序
	if ( Cutoff <= Right-Left ) {
	//此时Left是三个里最小的，Right是最大的，主元放在[Right-1]
		Pivot = Median3( A, Left, Right );
		i = Left; j = Right – 1;
		for( ; ; ) { 
			while ( A[ ++i ] < Pivot ) { } //左边小于主元，向右移动i
			while ( A[ ––j ] > Pivot ) { } //右边大于主元，向左移动j
			if ( i < j )  
				Swap( &A[i], &A[j] );
			else break;
		} 
		Swap( &A[i], &A[ Right-1 ] );
		Quicksort( A, Left, i-1 );  //左边递归
		Quicksort( A, i+1, Right ); //右边递归
	}
	else //规模小，用插入排序
		Insertion_Sort( A+Left, Right-Left+1 );
}

//上米娜函数接口不合符要求，需要一个壳来包装下
void Quick_Sort(ElementType A[],int N) 
{ 
	Quicksort( A, 0, N-1 ); 
}

C语言代码：快速排序-直接调用库函数

/* 快速排序 - 直接调用库函数 */

#include 

/*---------------简单整数排序--------------------*/
int compare(const void *a, const void *b)
{ /* 比较两整数。非降序排列 */
    return (*(int*)a - *(int*)b);
}
/* 调用接口 */ 
qsort(A, N, sizeof(int), compare);
/*---------------简单整数排序--------------------*/


/*--------------- 一般情况下，对结构体Node中的某键值key排序 ---------------*/
struct Node {
    int key1, key2;
} A[MAXN];
 
int compare2keys(const void *a, const void *b)
{ /* 比较两种键值：按key1非升序排列；如果key1相等，则按key2非降序排列 */
    int k;
    if ( ((const struct Node*)a)->key1 < ((const struct Node*)b)->key1 )
        k = 1;
    else if ( ((const struct Node*)a)->key1 > ((const struct Node*)b)->key1 )
        k = -1;
    else { /* 如果key1相等 */
        if ( ((const struct Node*)a)->key2 < ((const struct Node*)b)->key2 )
            k = -1;
        else
            k = 1;
    }
    return k;
}
/* 调用接口 */ 
qsort(A, N, sizeof(struct Node), compare2keys);
/*--------------- 一般情况下，对结构体Node中的某键值key排序 ---------------*/

C语言代码：快速排序-自己实现

/* 快速排序 */

ElementType Median3( ElementType A[], int Left, int Right )
{ 
    int Center = (Left+Right) / 2;
    if ( A[Left] > A[Center] )
        Swap( &A[Left], &A[Center] );
    if ( A[Left] > A[Right] )
        Swap( &A[Left], &A[Right] );
    if ( A[Center] > A[Right] )
        Swap( &A[Center], &A[Right] );
    /* 此时A[Left] <= A[Center] <= A[Right] */
    Swap( &A[Center], &A[Right-1] ); /* 将基准Pivot藏到右边*/
    /* 只需要考虑A[Left+1] … A[Right-2] */
    return  A[Right-1];  /* 返回基准Pivot */
}

void Qsort( ElementType A[], int Left, int Right )
{ /* 核心递归函数 */ 
     int Pivot, Cutoff, Low, High;
      
     if ( Cutoff <= Right-Left ) { /* 如果序列元素充分多，进入快排 */
          Pivot = Median3( A, Left, Right ); /* 选基准 */ 
          Low = Left; High = Right-1;
          while (1) { /*将序列中比基准小的移到基准左边，大的移到右边*/
               while ( A[++Low] < Pivot ) ;
               while ( A[--High] > Pivot ) ;
               if ( Low < High ) Swap( &A[Low], &A[High] );
               else break;
          }
          Swap( &A[Low], &A[Right-1] );   /* 将基准换到正确的位置 */ 
          Qsort( A, Left, Low-1 );    /* 递归解决左边 */ 
          Qsort( A, Low+1, Right );   /* 递归解决右边 */  
     }
     else InsertionSort( A+Left, Right-Left+1 ); /* 元素太少，用简单排序 */ 
}

void QuickSort( ElementType A[], int N )
{ /* 统一接口 */
     Qsort( A, 0, N-1 );
}

小测验

1、快速排序是稳定的算法。 (错误)