数据结构基础：P10.2-排序(二)---＞表排序

本系列文章为浙江大学陈越、何钦铭数据结构学习笔记，前面的系列文章链接如下：
数据结构基础：P1-基本概念
数据结构基础：P2.1-线性结构—＞线性表
数据结构基础：P2.2-线性结构—＞堆栈
数据结构基础：P2.3-线性结构—＞队列
数据结构基础：P2.4-线性结构—＞应用实例：多项式加法运算
数据结构基础：P2.5-线性结构—＞应用实例：多项式乘法与加法运算-C实现
数据结构基础：P3.1-树(一)—＞树与树的表示
数据结构基础：P3.2-树(一)—＞二叉树及存储结构
数据结构基础：P3.3-树(一)—＞二叉树的遍历
数据结构基础：P3.4-树(一)—＞小白专场：树的同构-C语言实现
数据结构基础：P4.1-树(二)—＞二叉搜索树
数据结构基础：P4.2-树(二)—＞二叉平衡树
数据结构基础：P4.3-树(二)—＞小白专场：是否同一棵二叉搜索树-C实现
数据结构基础：P4.4-树(二)—＞线性结构之习题选讲：逆转链表
数据结构基础：P5.1-树(三)—＞堆
数据结构基础：P5.2-树(三)—＞哈夫曼树与哈夫曼编码
数据结构基础：P5.3-树(三)—＞集合及运算
数据结构基础：P5.4-树(三)—＞入门专场：堆中的路径
数据结构基础：P5.5-树(三)—＞入门专场：File Transfer
数据结构基础：P6.1-图(一)—＞什么是图
数据结构基础：P6.2-图(一)—＞图的遍历
数据结构基础：P6.3-图(一)—＞应用实例：拯救007
数据结构基础：P6.4-图(一)—＞应用实例：六度空间
数据结构基础：P6.5-图(一)—＞小白专场：如何建立图-C语言实现
数据结构基础：P7.1-图(二)—＞树之习题选讲：Tree Traversals Again
数据结构基础：P7.2-图(二)—＞树之习题选讲：Complete Binary Search Tree
数据结构基础：P7.3-图(二)—＞树之习题选讲：Huffman Codes
数据结构基础：P7.4-图(二)—＞最短路径问题
数据结构基础：P7.5-图(二)—＞哈利·波特的考试
数据结构基础：P8.1-图(三)—＞最小生成树问题
数据结构基础：P8.2-图(三)—＞拓扑排序
数据结构基础：P8.3-图(三)—＞图之习题选讲-旅游规划
数据结构基础：P9.1-排序(一)—＞简单排序(冒泡、插入)
数据结构基础：P9.2-排序(一)—＞希尔排序
数据结构基础：P9.3-排序(一)—＞堆排序
数据结构基础：P9.4-排序(一)—＞归并排序
数据结构基础：P10.1-排序(二)—＞快速排序

---

一、算法概述

什么情况下用到表排序：

当你的待排元素不是一个简单的整数，而是一个庞大的结构(比如说是一本书、一部电影)时，你需要移动一个元素的时间是不能忽略不计的。于是我们如果简单的调一些排序算法，它们都涉及到频繁的元素交换移动。那么当你要移动的元素是一部电影的时候，你要不停的把他们移来移去，这就变成了很恐怖的一件事情。那么表排序就是这样一种算法：你在排序的过程中实际上是不需要移动这些原始数据的，你要移动的只是指向他们位置的那些指针。不移动元素本身,而只移动指针的这种排序方法叫做间接排序。

算法思路：

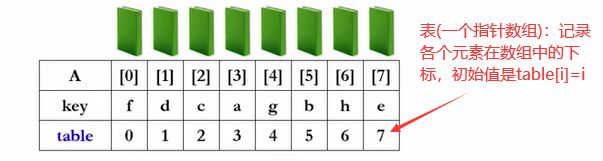
在这我们给了一个待排序列A，A的每一个元素都有一个关键字，我们要把它按照关键字来排序

我们先定义一个table，这个表是一个指针数组，记录元素在数组中的下标，在初始的时候这个table[i]=i。

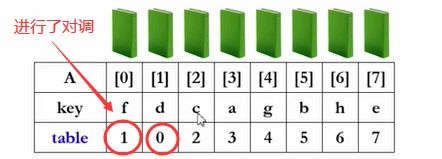
于是，我们对这个数组调用任何一种排序算法(我就离就用插排序)，来看看是怎么执行的。在做插入排序的时候，我们假设第一张牌已经在手里了，然后比较第二张牌跟第一张牌的大小。A[table[1]]的key=d，小于A[table[0]]的key=f，所以他们应该有一个交换。但是我不交换这两本书，我交换表里面指向这两本书的指针。

下一张牌摸进来的是c，我们发现A[table[2]]的key=c小于A[table[1]]的key=f和A[table[0]]的key=d，于是table中1和0要往后错一位，2要移到它们前面。

下一张牌摸进来的是a，发现a小于前面的f、d、c，所以3放他们前面，2、1、0往后挪。

下一张牌摸进来的是g，发现A[table[4]]的key=g大于它前面的A[table[3]]的key=f，所以不用动，继续看下一个。
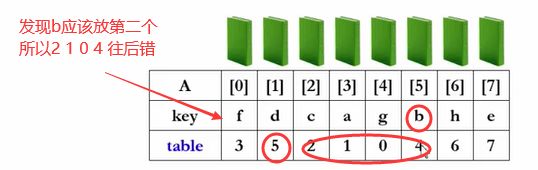
下一张牌摸进来的是b，应该放在第二个，所以2、1、0、4往后挪，把5放进去。

下一张牌摸进来的是h，发现A[table[6]]的key=h大于它前面的A[table[5]]的key=g，所以不用动，继续看下一个。
下一张牌摸进来的是e，应该放在第五个，所以0、4、6往后挪，把7放进去。

最后算法结束，输出如下：
A[table[0]]=A[3]=a
A[table[1]]=A[5]=b
A[table[2]]=A[2]=c
A[table[3]]=A[1]=d
A[table[4]]=A[7]=e
A[table[5]]=A[0]=f
A[table[6]]=A[4]=g
A[table[7]]=A[6]=h

二、物理排序

在表排序完成以后，如果在某种情况下我们必须要对所有的元素做一个物理排序，也就是我最后非得把那些书物理上按照顺序给排出来，这时我们有一种非常聪明的方法可以在线性的时间复杂度内完成这件事情。它利用了一个非常重要的原理：N个数字的排列一定是由若干个独立的环组成的

N个数字的排列一定是由若干个独立的环组成的

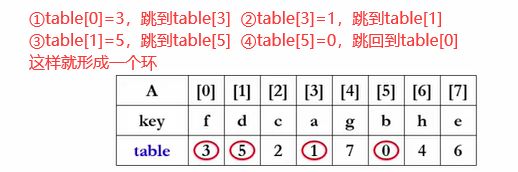
我们还是回到刚才的那个例子，这是我们表排序完了以后的结果

我们来从table[0]开始。table[0]=3，跳到table[3]。table[3]=1，跳到table[1]。table[1]=5，跳到table[5]。table[5]=0，又回到了原始点。这四个数字就组成了一个环

继续找下一个环，发现table[2]=2，就是它自己，于是这个环就只包含一个元素2。

继续找下一个环，发现table[4]=7，跳到table[7]。table[7]=6，跳到table[6]。table[6]=4，跳到回起点。这三个数字就组成了一个环。

我们发现三种不同颜色的环他们之间是没有交集的，这就是叫独立，即他们之间是互不相干的。

于是，我们在调整的时候就可以按照一个环一个环的方法来调整这些书的位置。

对于这个红色的环，我们可以想象这四本书排成一个环状，然后他们要错一下位而已。我先把第一本书拿下来，存在一个临时的地方。

空着的A[0]应该放A[table[0]]=A[3]=a，于是将A[3]放过去，并更新key，此时A[3]空着。

空着的A[3]应该放A[table[3]]=A[1]=d，于是将A[1]放过去，并更新key，此时A[1]空着

空着的A[1]应该放A[table[1]]=A[5]=b，于是将A[5]放过去，并更新key，此时A[5]空着

空着的A[5]应该放A[table[5]]=A[0]=f，于是将临时存储的A[0]放过去，并更新key，第一个环结束。在这个环里，这四本书的物理顺序对了。

问题：如何判断一个环的结束？

每访问一个空位i后，就令table[i]=i，代表这个元素已经放到了正确的位置，比如那个单独的绿色环2，A[table[2]]=A[2]，它的位置就是正确的。当发现table[i]==i时，环就结束了。

复杂度分析

最好情况：初始即有序
最坏情况：
有$\lfloor N/2\rfloor$个环，每个环包含2个元素
需要$\lfloor 3N/2\rfloor$次元素移动：直接调用swap的时候，我们必须要走三步：把一本书放到一个临时的位置、然后另外一本书放过去、然后临时位置这本书再放上去
复杂度：$T=O(mN)$ ，m是每个A元素的复制时间。

小测验

1、给定A[]={46, 23, 8, 99, 31, 12, 85}，调用非递归的归并排序加表排序执行第1趟后，表元素的结果是：

A. 0, 1, 2, 3, 4, 5, 6
B. 1, 0, 3, 2, 6, 5, 4
C.  1, 0, 2, 3, 5, 4, 6
D. 0, 2, 1, 4, 3, 5, 6

答案：C

2、给定A[]={23, 46, 8, 99, 31, 12, 85}，调用表排序后，表元素的结果是：

A. 1, 2, 3, 4, 5, 6, 7
B. 2, 0, 3, 5, 1, 4, 6
C. 3, 6, 1, 5, 2, 7, 4
D. 2, 5, 0, 4, 1, 6, 3

答案:D