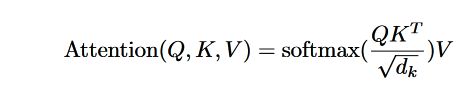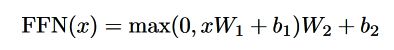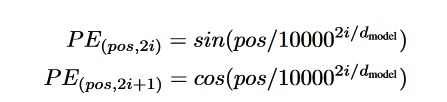Attention is all you need
Abstract
本文中提出了transformer模型,完全依靠attention机制,没有使用循环网络或者卷积网络。
Transformer在训练中可以更好的并行化,并且需要更少的训练时间。
Transformer可以很好的泛化到其他的任务中。
1 Introduction
在序列模型和转换问题(transduction problem)上,最优的策略是 循环神经网络、LSTM和gated recurrent 神经网络。有大量的工作是关于循环语言模型和 encoder-decoder架构。
在循环神经网络中, h t − 1 h_{t-1} ht−1 和input中 t 位置上数据共同计算 h t h_t ht ,这就阻碍了训练过程的并行化。
注意力机制,可以使得计算词之间的相关性时,不在乎距离的远近。相反,使用循环神经网络,如果两个词之间有相关性但是相隔很远,中间的计算路径会非常的长。在以往的工作中,注意力机制和循环神经网络是结合使用的。
本文中提出了transformer模型,完全依靠attention机制,没有使用循环网络或者卷积网络。
2 Background
在以的序列模型中,很难计算相隔较远的位置上的相关性(dependencies). 但是transfomer对任意位置上的相关性计算都是通过常量数量的操作来计算的。
这里使用了自注意力机制,所谓的自注意力机制是指 K Q V都是原本的相同向量。(当然,使用多头注意力机制时,会对K Q V进行投影,K Q V不再是原本的向量)
3 模型架构
encoder-decoder架构
encoder 输入是一系列的符号表示 ( x 1 , x 2 , . . . , x n ) (x_1,x_2,...,x_n) (x1,x2,...,xn) ,将其映射到一个组向量Z = ( z 1 , z 2 , z 3 , . . . , z n ) (z_1,z_2, z_3,...,z_n) (z1,z2,z3,...,zn) . z i z_i zi 表示一个向量
decoder 根据Z生成一系列的符号, ( y 1 , y 2 , . . . , y m ) (y_1,y_2,...,y_m) (y1,y2,...,ym). decoder每次只生成一个符号。
decoder解码是一个自回归的过程。
auto-regressive
将之前生成的符号,作为输出来生成下一个输出,直到生成所有的输出。
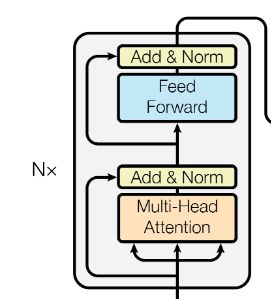
3.1 Encoder Decoder 堆叠
Encoder 由 N=6 个完全相同的层堆叠而成,每个encoder层由两个子层构成。
- 第一个子层是 multi-head 注意力机制
- 第二个子层是一个简单的 positon-wise的全连接网络
在每个子层后,应用了残差链接 和 layer normalization,每个子层可以看作 L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm(x + Sublayer(x)) LayerNorm(x+Sublayer(x)) .
为了在计算残差时更加方便,统一了计算过程中的维度。 每个子层的输出维度和embeding层输出的维度都是一样得,这里设为 d m o d e l = 512 d_{model} = 512 dmodel=512
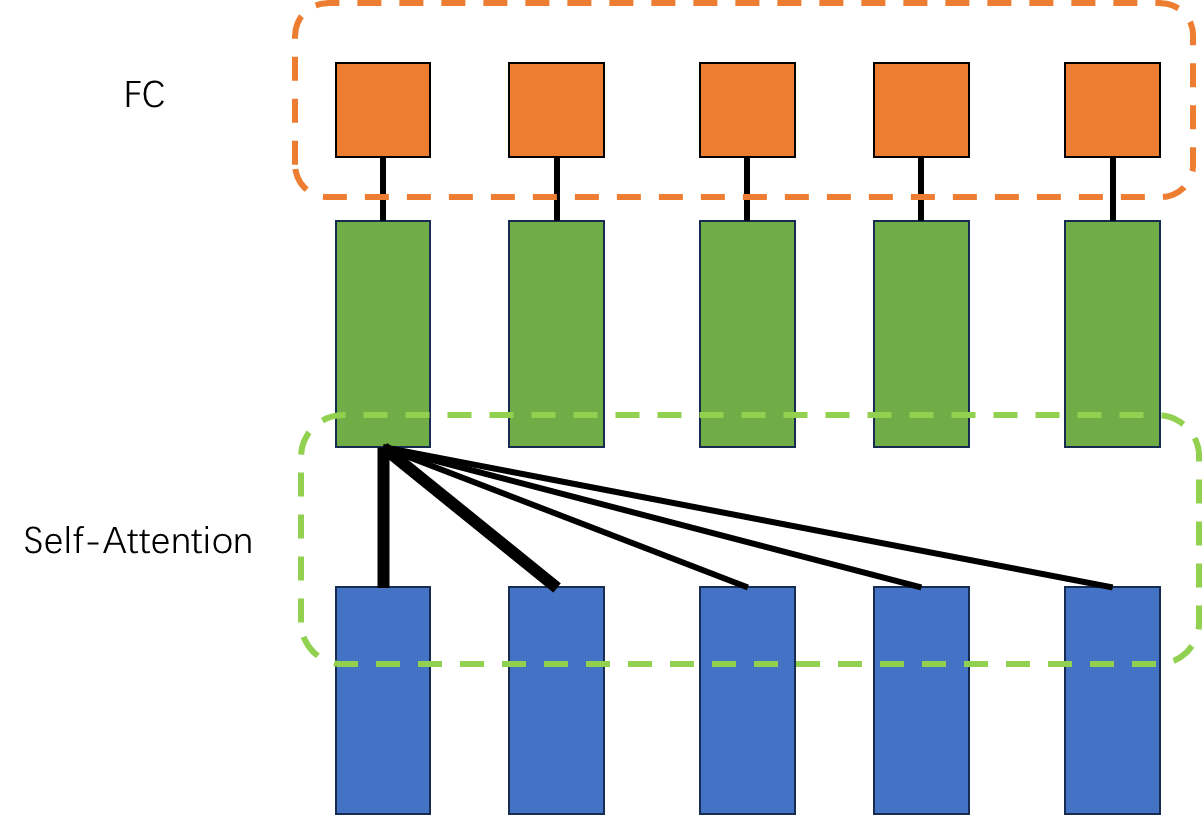
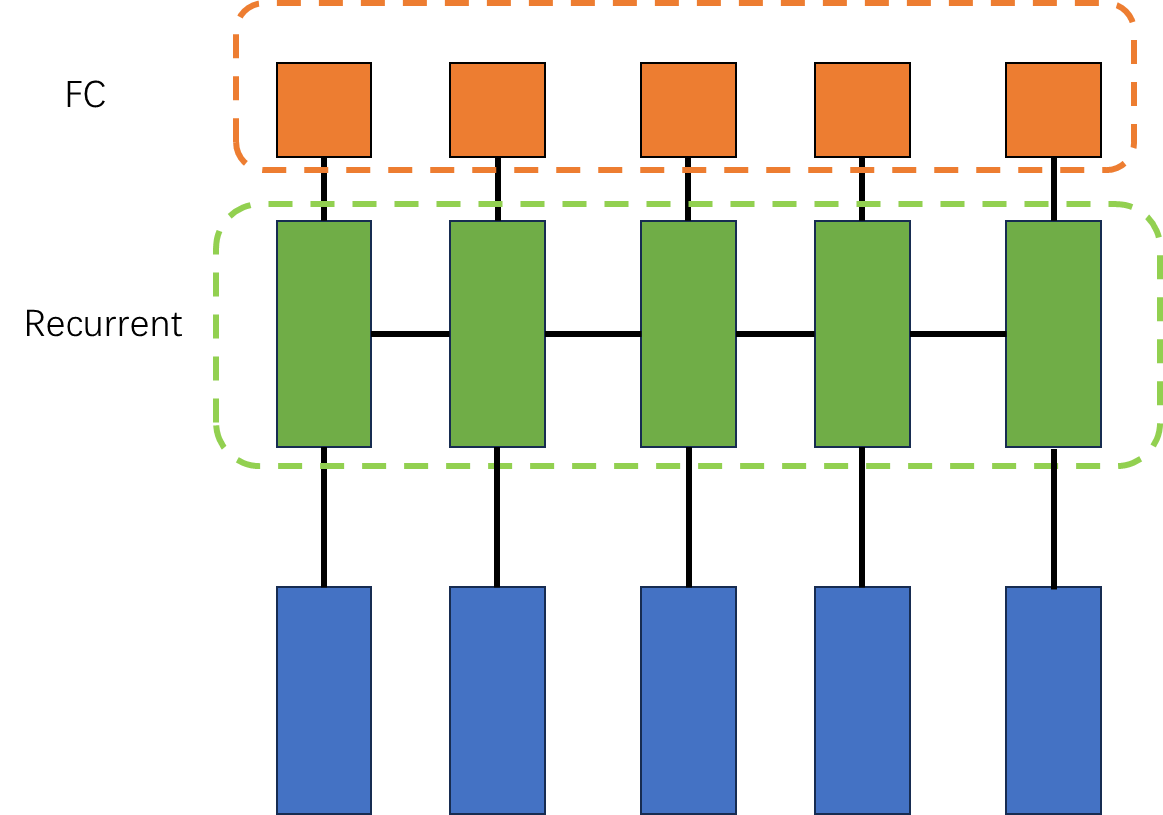
下面的两张图可以凸显 self-attention 和 rnn之间的区别。
他们能够学习的部分都是全连接网络部。 但是attention中输入FC的向量会获得与他有依赖的向量的信息。这个计算需要常量级的计算。 但是对于RNN,一个向量若想获取与他相关的向量的信息,需要经过一长串的计算。
positon-wise FC是指,每个位置的各个向量使用的FC参数是完全相同的。
Decoder
Decoder 也是由 N=6 个完全相同的层堆叠而成的堆叠而成的。
decoder还多了一层 masked-multihead 注意力层。我们使用的自回归机制,会将之前生成的结果作为输入,再输出新的结果。 当我们训练transfomer时,向 decoder中直接输入一整串目标结果显然是不合适的,这会导致 i 位置上的输出会看到i位置之后的输出,这和生成过程不相符。因此加上mask,使得 i 位置上的输出只能看到 i位置之前的结果。
要想实现mask效果,可以将被掩盖的权重设为一个极小值。
3.2 Attention
Attention 计算过程中值要通过 query, keys, values 三种类型的向量进行计算,本质上就是value向量的一种加权和。通过 query和 keys向量计算权重。
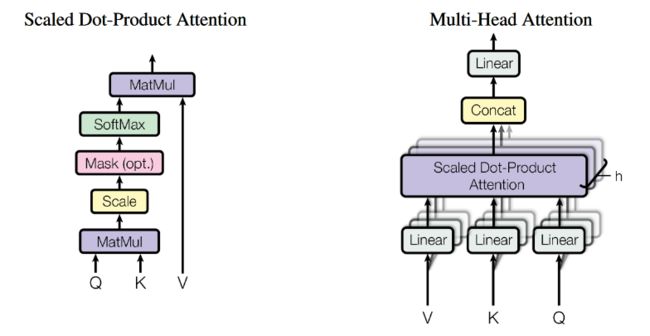
3.2.1 Scaled Dot-Product Attention
有两种计算 attention的主流方式,
- 一是累加的方式计算 attention
- 另一种是点成的方式计算 attetion
这里用的就是点成的方式,此外这里将点乘的结果又除以 d k \sqrt{d_k} dk。是因为如果乘积的值比较大,会导致将softmax推向趋近于1的极端,梯度变小,收敛速度变慢。
使用点乘的当时计算 attention,是因为矩阵乘法的计算效率比较高。
3.2.2 多头注意力机制 Multi-head attention
在卷积网络中,有类似多通道的机制。通过multi-head attention可以实现多通道的效果。
与其直接将 d m o d e l d_{model} dmodel维的key query value向量直接拿来做attention,我们将 k q v进行线性的投影,将投影的结果用来做 attention。我们可以对 k q v进行多次投影,来做多次attention。再将多头注意力就算的结果进行拼接。
我们将 K Q投影到 d k d_k dk 维度,将V投影到 d v d_v dv维度。
因为多头注意力机制,我们会学习投影所用到的W矩阵,因此进行self-attention计算的 k q v不再是完全相同的向量了。
3.3 Position-wise Feed-Forward Networks
positon-wise 是指,每个位置的各个向量使用的FFN的参数是完全相同的。
3.4 Embeding
embeding 层将输入的token转混成 d m o d e l d_model dmodel 维度的向量。
计算输出时使用一个线性转换和softmax来将output转换为 next-token的概率。
3.5 Positional Encoding
在attention的计算过程中,无论在序列中距离有多远,计算attention的步骤都是一样的,这就导致,若干两个token相同不同位置的计算结果是一样的。
我们在数据中注入序列信息,使用positional encoding,在这里使用遇险方式
pos 是在序列中的位置, 2i 、2i+1 是在 d m o d e l d_{model} dmodel 维度中的位置
Conclusion
Transformer是第一个完全依靠注意力机制的序列转换模型。
在encoder-decoder中,没有使用循环网络而是采用了注意力机制,
在翻译任务上,Transformer的训练要更快。
在未来,注意力模型可以被应在其他的任务上。