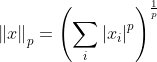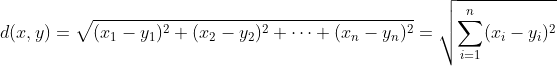【深度学习】数学基础——线代
目录
0、基础
1、基本运算和基本概念
2、范数
3、向量基概念及运算
4、行列式及特殊矩阵
5、奇异值分解(SVD)
6、基向量及线性相关性等
7、线性变换
8、特征方程与相似矩阵
9、其他资料
0、基础
- 标量:0维数据,如常数0、1、2等单个数字。
- 向量:1维数据,如(1, 2),(2,3),(2,3,4)等点。
- 矩阵:2维数据,如[[1,3],[2,8]] 的2维数组等。
- 张量:可以简单的理解为Pytorch、TensorFlow框架等对向量、矩阵数据特殊称呼。
1、基本运算和基本概念
- 加、减、数加、数减、数乘
- 叉乘(矩阵/张量的乘法):行乘以列。
# 可用以下方法实现叉乘
a @ b #Python方法
torch.matmul(a, b) #Pytorch框架常用- 矩阵的点乘:两矩阵形状相同,对应位置点相乘。(注:和向量的点乘不同)
- 转置
- 逆:逆运算相当于矩阵的除法运算,非奇异方阵才有逆
torch.inverse(a) # torch框架
np.linalg.inv(a) # numpy框架 - 伪逆:伪逆是逆的推广,去除了方阵的限制
2、范数
范数是用来衡量数的大小
- 零范数:向量中非零元素的个数
- 一范数:向量中绝对值之和
║A║ = max{ ∑|ai1|,∑|ai2|,……,∑|ain| } (列和范数,A每一列元素绝对值之和的最大值)
║A║ = max{ ∑|a1i|,∑|a2i|,……,∑|ani| } (行和范数,A每一行元素绝对值之和的最大值)
- 二范数:向量的模
- 无穷范数:向量中的最大值
- 范数计算公式
- 归一化(部分):
- 最大值归一化:每个值除以无穷范数
- 二范数归一化:每个值除以二范数
3、向量基概念及运算
- 内积与投影:对应位置相乘相加。内积的含义为向量a在向量b上的投影;反应两个向量的相似程度,不可以直接用来衡量相关性。
- 余弦相似度:
分母的意义:除以各自的模使其在同一坐标系或同一基向量中。
- 欧氏距离
缺点:值域为[0,+∞),不能直接比较;大小很模糊,不能度量
优点:简单
对两向量做二范数归一化所得的欧式距离等价于余弦相似度。
- 相关性
- 线性相关:
正相关:两向量夹角小于90°
负相关:两向量夹角大于90° - 线性无关:两向量夹角等于90°
扩展:向量相似度的度量
4、行列式及特殊矩阵
- 行列式: 二维为面积和三维及以上为体积。计算方式:
np.linalg.det(a) # Numpy框架
b.det() # Torch框架 b为torch.tensor()创建方阵;输入需要为float-
特殊矩阵
- 方阵:矩阵的行数和列数相同
- 0、1矩阵
# 创建1矩阵
np.ones((3, 3))
torch.ones(3, 3)
# 创建0矩阵
np.zeros((3, 3))
torch.zeros(3, 3) 3. 单位矩阵
np.eye(n, m) # n, m为单位矩阵维度
torch.eye(n, m)4. 下三角矩阵:和其他矩阵作运算可以起到遮挡作用
np.tri(n, m) n, m为单位矩阵维度
torch.tril(torch.ones(n, m))5. 奇异矩阵和非奇异矩阵
奇异矩阵:方阵且行列式为0
6. 斜对角矩阵: 主对角线存在非0元素,其余元素全为0
np.diag([data])
torch.diag(torch.tensor([data])) # [data]为主对角线元素,由列表构成 7. 稀疏矩阵
若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律
非零元素的总数比上矩阵所有元素总数的值小于等于0.05
5、奇异值分解(SVD)
将非方阵分解为3个矩阵相乘。
上图为喜欢同一类型或相近类型书籍的一批用户对不同书籍的打分,我们现在需要通过对已知打分表X预测第一个用户对第4本书的购买欲望。则可以通过对矩阵X的进行SVD,可得到三个矩阵(上图缺少Σ权重矩阵)U、Σ、V,其中 Σ为特征值矩阵、U为用户的偏向权重矩阵、V为书内容受欢迎程度偏向权重矩阵。那么我们就可以通过U、V矩阵预估出第一个用户对第4本书的购买欲望。
import numpy as np
a = np.array([[12,3], [2,3],[7, 98]]) # 形状为(3,2)
u,s,v = np.linalg.svd(a)
print(u)
print(s)
print(v)
z = np.zeros((3,2))
z[0][0] = s[0]
z[1][1] = s[1]
print(z)
print(u@z@v)
# u
[[ 0.03974454 0.98792384 -0.149756 ]
[ 0.03196212 0.14854076 0.98838963]
[ 0.99869855 -0.04406961 -0.02567246]]
# s等价于下面的z
[98.37631919 11.87854464] #对角矩阵 形状应和原矩阵相同(3,2)
# v
[[ 0.07656059 0.99706493]
[ 0.99706493 -0.07656059]]
# z为将s扩张成矩阵的结果
[[98.37631919 0. ]
[ 0. 11.87854464]
[ 0. 0. ]]
# a = u@z@v
[[12. 3.]
[ 2. 3.]
[ 7. 98.]]
6、基向量及线性相关性等
- 定义:【百度百科——基向量】
- 作用:划分特征空间。
- 理解:如直角坐标系中的x, y轴表特征标准,本质是向量,还表明了特征方向。
- 标准正交基:【百度百科——标准正交基】
- 完备正交基:基向量垂直且完美划分特征空间。
研究相关性的目的:一就是找到轴/基向量,之后进行特征分解,找到特征方向;二是衡量相关性
- 什么是线性?最形象化的理解为:在二维空间内是一条直线,在三维空间内是一个平面(此平面也被称为超平面),更高维的统称为超平面。
7、线性变换
- 基础
- 线性空间:一组正交基向量构成的空间(二维的xoy坐标系)
- 线性变换:对线性空间的数据进行操作——平移、旋转、缩放。矩阵乘法的实质是对n个向量同时做一系列的线性变换。
拓展:
- 【马同学——线性变换】
- 【线性变换(一)直观理解线性变换】
8、特征方程与相似矩阵
- 特征方程
- 定义:设A为n阶方阵,若存在数λ和非零向量x使得 Ax = λx则称λ是A的一个特征值,x为A的对应于特征λ的特征向量。(其中λ可以为复数)
- 含义:
- 相似矩阵
- 定义:设A,B为n阶矩阵,如果有n阶可逆矩阵P存在,使得AP=PB则称矩阵A与B相似,记为A~B。
- 含义:
9、其他资料
- 【3Blue1Brown】含线代讲解
- 【麻省理工 数学 线性代数 Linear Algebra】