DBO优化TCN的电力负荷预测,附MATLAB代码
今天为大家带来一期基于DBO-TCN的电力负荷预测。不得不说,TCN在时序数据中的预测效果在一定程度上要优于LSTM。
原理详解
文章对TCN网络的五个参数进行优化,分别是:
正则化参数,学习率,滤波器个数,滤波器大小,区块数。这五个参数属于TCN网络中比较重要的几个参数,参数的选择会影响最后的精度。
采用蜣螂优化TCN,参数设置范围分别是:
| 正则化参数 | [0.001 0.1] |
| 学习率 | [ 0.0001 0.01] |
| 滤波器个数 | [20 100] |
| 滤波器大小 | [2 10] |
| 区块数 | [2 10] |
将DBO种群数设置为:30,迭代次数设置为30。
数据准备
对电力负荷数据进行处理
本次数据包含负荷值,温度,湿度,风速,压强,降水量,能见度,水汽压和体感温度,部分数据截图如下:
选取1200个样本作为训练集,每个样本组成为:当天24个小时的全部数据,因此训练集的输入数据大小为1200*216,其中216=24*9,24代表24个小时,9代表9个特征。训练集的输出数据大小为:1200*1。1代表未来一小时的负荷值。
选取300个样本作为测试集,同理,测试集的输入数据大小为300*216,训练集的输出数据大小为:300*1。
结果展示
采用TCN网络对电力负荷数据进行训练和预测
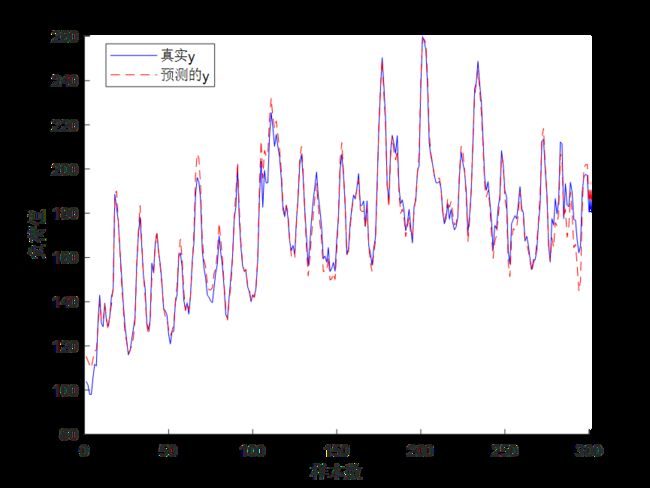
TCN的预测结果如下:
可以看到,未优化的TCN网络预测效果不是很理想,但是相比于上一期给出的LSTM的预测效果已经好很多了。
DBO-TCN模型的预测效果如下:
误差对比图如下:
可以看到DBO-TCN预测效果有了明显提升,DBO-TCN的MSE误差为13.821,相比于未优化TCN的23.238有了很大提升!
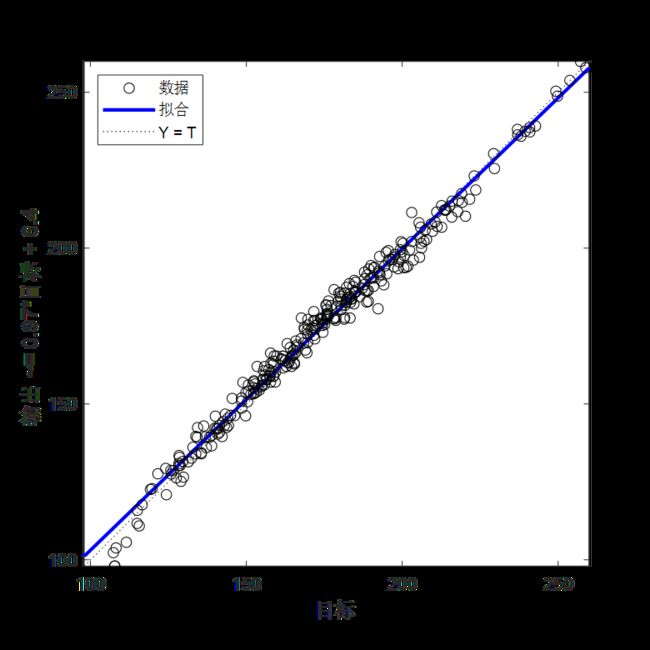
DBN-TCN的回归拟合图:
误差直方图:
![]()
部分代码
% 网络训练
net0 = trainNetwork(inputn,outputn,lgraph,options0 );
an0 = net0.predict(inputn_test);
test_simu0=mapminmax('reverse',an0,outputps); %把仿真得到的数据还原为原始的数量级
%误差指标
error0 = output_test - test_simu0;
mse0=mse(output_test,test_simu0)
%% 标准TCN神经网络作图
figure
plot(output_test,'b-','markerfacecolor',[0.5,0.5,0.9],'MarkerSize',6)
hold on
plot(test_simu0,'r--','MarkerSize',6)
title(['TCN的mse误差:',num2str(mse0)])
legend('真实y','预测的y')
xlabel('样本数')
ylabel('负荷值')
box off
set(gcf,'color','w')
%% 调用DBO优化TCN
disp('调用DBO优化TCN......')
% DBO优化参数设置
SearchAgents = 20; % 种群数量 30
Max_iterations = 30; % 迭代次数 30
lowerbound = [0.001 0.0001 20 2 2]; %五个参数的下限分别是正则化参数,学习率,滤波器个数:numFilters,滤波器大小:filterSize,区块数:numBlocks
upperbound = [0.1 0.01 100 10 10]; %五个参数的上限
dimension = length(lowerbound);%数量,即要优化的TCN参数个数
[fMin,Best_pos,Convergence_curve,bestnet] = DBOforTCN(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,inputn,outputn,inputn_test,outputps,output_test,numFeatures,outputSize);
L2Regularization = Best_pos(1,1); % 最佳L2正则化系数
InitialLearnRate = Best_pos(1,2) ;% 最佳初始学习率
numFilters = fix(Best_pos(1,3));
filterSize = fix(Best_pos(1,4));
numBlocks = fix(Best_pos(1,5));
disp(['最优参数:',num2str(Best_pos)])
disp('优化结束,将最佳net导出并用于测试......')
setdemorandstream(pi);
%% 对测试集的测试
an = bestnet.predict(inputn_test);
test_simu = mapminmax('reverse',an,outputps);
error = test_simu-output_test;
msee = mse(output_test,test_simu);
figure
hold on
plot(test_simu,'g')
plot(output_test,'b')
legend('DBO-TCN预测值','实际值')
ylabel('预测结果')
xlabel('预测样本')
title(['DBO-TCN的mse误差:',num2str(msee)])
box off
set(gcf,'color','w')
figure
plot(abs(error),'g-*')
hold on
plot(abs(error0),'-or')
title('预测误差对比图','fontsize',12)
xlabel('预测样本','fontsize',12)
ylabel('误差绝对值','fontsize',12)
legend('DBO-TCN','TCN')
%% 回归图与误差直方图
figure;
plotregression(test_simu,output_test,['优化后回归图']);
set(gcf,'color','w')
figure;
ploterrhist(test_simu-output_test,['误差直方图']);
set(gcf,'color','w')
%% 打印出评价指标
% 预测结果评价
ae= abs(test_simu-output_test);
rmse = (mean(ae.^2)).^0.5;
mse = mean(ae.^2);
mae = mean(ae);
mape = mean(ae./test_simu);
R = corr(output_test,test_simu);
R2 = 1 - norm(output_test - test_simu)^2 / norm(output_test-mean(output_test ))^2;
disp('预测结果评价指标:')
disp(['RMSE = ', num2str(rmse)])
disp(['MSE = ', num2str(mse)])
disp(['MAE = ', num2str(mae)])
disp(['MAPE = ', num2str(mape)])
disp(['相关系数R = ', num2str(R)])
disp(['决定系数R^2为: ',num2str(R2)])代码获取
完整代码获取,后台回复关键词:
DBOTCN