排序算法-归并排序

排序算法-归并排序

算法思想

归并：将两个或者两个以上的有序表组合成一个新的有序表的过程。假定待排序表中含有n个记录，则可以看成是n个有序的子表，每个子表的长度为1，然后两两归并，得到$\lceil n/2\rceil$个长度为2或1的有序表；再两两归并，如此一直重复，直到合并成一个长度为n的有序表为止，这种排序方法称为2路归并排序。

2路归并排序的过程如下图所示。

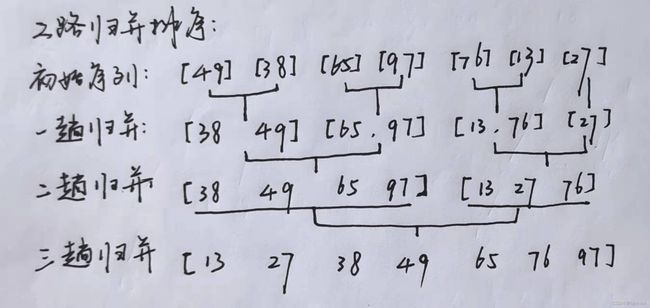
从归并的过程不难看出，其代码实现可以基于分治思想递归实现。其基本问题是如何实现两个有序序列的归并操作，该操作可以通过使用辅助数组以及双指针的方式实现。

合并两个有序数组的代码：
其中nums为待排序序列，temp为辅助数组，其长度与nums一致，low为要合并的左子序列的起点，mid为要合并的右子序列的起点。

public static void Merge(int[] nums,int[] temp, int low,int mid, int high){
        // 表的两段nums[low...mid]与nums[mid+1...high]都有序，将两段进行有序归并
        for(int i=low;i<=high;++i)  // 将nums[low...high]元素复制到temp中，防止之后修改nums产生错误
            temp[i] = nums[i];
        int i,j,k;
        for(i=low,j=mid+1,k=i;i<mid+1 && j<=high;++k){
            if(temp[i]<temp[j])    //比较nums中的low和mid+1为起点的子序列元素
                nums[k] = temp[i++];  //将较小值复制到nums中，使得归并后的序列有序
            else{
                nums[k] = temp[j++];
            }
        }
        while(i<mid+1) nums[k++] = temp[i++];  // 若左表未遍历完，将左表剩余元素复制到nums剩余位置
        while(j<=high) nums[k++] = temp[j++];  // 若右表未遍历完，将右表剩余元素复制到nums剩余位置
        // 以上while循环只有一最终会满足条件
    }

Merge()的功能是将前后相邻的两个有序表归并为一个有序表的算法。设两段有序表$nums[low...mid]$和$nums[mid+\mathrm{1...}high]$存放在同一顺序表中相邻的位置上，先将它们复制到辅助数组temp中。每次从对应temp中的两个段取出一个记录进行关键字比较，将较小者放入nums中，当数组temp中有一段的下标超出其对应的表长时（即该段的所有元素已经完全复制到nums中），将另一段的剩余部分直接复制到nums中。

归并排序

分解：将含有n个元素的待排序表分成各含n/2个元素的子表，采用2-路归并排序算法对两个子表递归地进行排序；
合并：合并两个已排序的子表得到排序结果。

完整代码：

package com.sort;

public class MergeSort {
    public static void main(String[] args) {
        int[] nums = {3,8,4,5,6,8,9,0,1};
        int[] temp = new int[nums.length]; //创建辅助数组，方便之后进行有序序列归并
        mergesort(nums,temp,0,nums.length-1);
        for(int num:nums){
            System.out.print(num+" ");
        }
    }
    public static void mergesort(int[] nums,int[] temps,int low,int high){
        if(low<high){
            int mid = (low + high) /2;  // 从中间划分两个西序列
            mergesort(nums,temps,low,mid);  // 对左侧子序列进行递归排序
            mergesort(nums,temps,mid+1,high);  // 对右侧子序列进行递归排序
            Merge(nums,temps,low,mid,high);   //合并左右有序子序列
        }
    }
    public static void Merge(int[] nums,int[] temp, int low,int mid, int high){
        // 表的两段nums[low...mid]与nums[mid+1...high]都有序，将两段进行有序归并
        for(int i=low;i<=high;++i)  // 将nums[low...high]元素复制到temp中，防止之后修改nums产生错误
            temp[i] = nums[i];
        int i,j,k;
        for(i=low,j=mid+1,k=i;i<mid+1 && j<=high;++k){
            if(temp[i]<temp[j])    //比较nums中的low和mid+1为起点的子序列元素
                nums[k] = temp[i++];  //将较小值复制到nums中，使得归并后的序列有序
            else{
                nums[k] = temp[j++];
            }
        }
        while(i<mid+1) nums[k++] = temp[i++];  // 若左表未遍历完，将左表剩余元素复制到nums剩余位置
        while(j<=high) nums[k++] = temp[j++];  // 若右表未遍历完，将右表剩余元素复制到nums剩余位置
        // 以上while循环只有一最终会满足条件
    }

}

复杂度分析

从2路归并排序的过程图中，易知2路归并的归并树形态就是一棵“倒立”的二叉树。

时间复杂度：
如果“归并树”树高为h，则归并排序所需要的归并趟数为h-1趟。二叉树的第h层最多有$2^{h-1}$个结点。若树高高为h，则应满足n<=$2^{h-1}$，因为树的第h层必然包含n个结点，即可得$h-1=\lceil lo{g}_{2}n\rceil$。又因为对n个元素进行归并排序，归并总趟数为h-1，即n个元素进行二路归并，归并趟数为$\lceil lo{g}_{2}n\rceil$。

每一趟的归并的时间复杂度，即Merge()的时间复杂度为$O(n)$，所以归并排序的时间复杂度就为 归并的时间复杂度 * 归并的趟数，即时间复杂度为$O(nlo{g}_{2}n)$。无论序列有序、无序，其时间复杂度都为$O(nlo{g}_{2}n)$。

空间复杂度：
辅助数组需要n个存储单元，空间复杂度为$O(n)$。
递归的深度为数的高度，空间复杂度为$O(lo{g}_{2}n)$。
整体来看，归并排序空间复杂度为$O(n)$。

稳定性：稳定。