（python）绘制科赫曲线以及利用科赫曲线举一反三

科赫曲线及其相关图形的绘制

---

---

前言

环境：

硬件: 微型计算机
软件: jupyter notebook
环境：python 3.8.1

介绍：

科赫曲线是一种像雪花的几何曲线，所以又称为雪花曲线，它是de Rham曲线的特例。科赫曲线是出现在海里格·冯·科赫的论文中，是分形曲线中的一种。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、绘制科赫曲线

绘制科赫曲线的代码如下：：

from turtle import *

def f(size , n):
    if n == 0:
        fd(size)
    else:
        for i in [0, 60, -120, 60]:
            left(i)
            f(size/3, n-1)

def main():
    setup(900, 900)
    speed(0)
    penup()
    goto(-200,150)
    pendown()
    pensize(2)
    pencolor("black")
    n = int(input("请输入科赫曲线的阶数："))
    hideturtle()
    done()
main()

这段代码使用Python的turtle模块绘制科赫曲线，其中包含一个递归函数 f() 和一个主函数 main()。

f(size, n)函数接受两个参数，分别是线段的长度size和科赫曲线的阶数n。如果阶数为0，则直接向前绘制线段；否则，通过循环语句分别旋转角度，并递归调用自身进行下一级别的绘制。

main()函数是程序的主要部分。在这里，我们进行一些设置，如窗口大小、绘图速度、背景色等。然后，通过调用turtle模块的函数实现绘图。接着使用循环语句绘制三个互相连接的科赫曲线。最后，我们填充图形的颜色，并隐藏海龟，完成整个绘制过程。

以下是一个示例，用于说明如何运行以上代码并理解其绘制过程：

当输入阶数为1时，即n = 1，
会绘制2个与相连的科赫曲线。

当输入阶数为2时，即n = 2，
会绘制2个与相连的科赫曲线，每个曲线中间都会出现一个三角形。

当输入阶数为3时，即n = 3，
会绘制2个与相连的科赫曲线，
每个曲线中间会出现4个三角形。

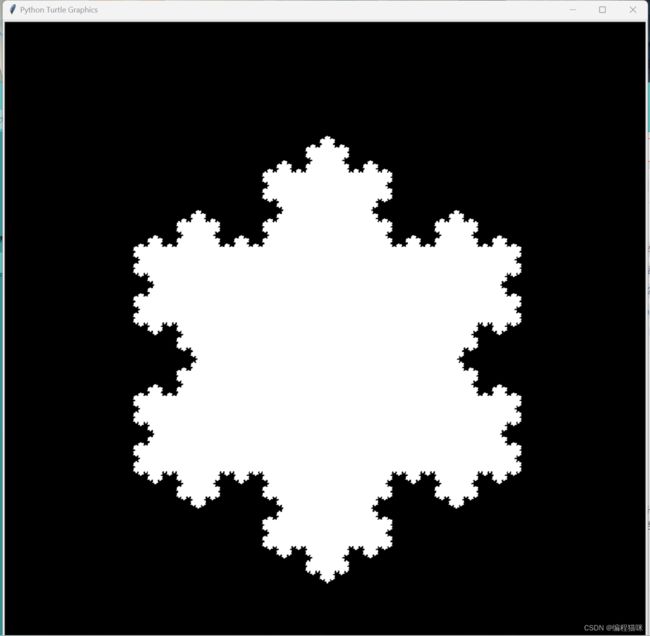
二、绘制科赫曲线的雪花效果

只需要改动部分编写思路，即可绘制出科赫曲线的雪花效果。

绘制科赫曲线的雪花效果的代码如下：

from turtle import *

def f(size , n):
    if n == 0:
        fd(size)
    else:
        for i in [0, 60, -120, 60]:
            left(i)
            f(size/3, n-1)

def main():
    setup(1000, 1000)
    speed(0)
    bgcolor("black")
    penup()
    goto(-300,150)
    pendown()
    pensize(2)
    pencolor("white")
    fillcolor("white")
    begin_fill()
    for i in range(2):
        f(600, 5)  # 五阶科赫曲线
        right(120)
    f(600, n)
    end_fill()
    hideturtle()
    done()

main()

下面对代码的不同部分进行详细解释：

1.导入模块：

from turtle import *
这行代码从turtle模块中导入所有的函数和类。

2. 绘制科赫曲线的递归函数 f(size, n)

参数 size 表示当前线段的长度。参数 n 表示科赫曲线的阶数。如果阶数 n 为0，则直接向前绘制线段的长度 size。否则，通过循环分别旋转角度，并以新的线段长度（原长度的1/3）递归调用函数 f()。

3.主函数 main()：

setup(1000, 1000) 设置绘图窗口的大小为1000x1000像素。
speed(0) 设置绘图速度为最快。
bgcolor(“black”) 设置背景颜色为黑色。
penup() 抬起画笔。
goto(-300, 150) 将海龟的位置移动到指定坐标点。
pendown() 放下画笔，开始绘制。
pensize(2) 设置画笔的宽度为2。
pencolor(“white”) 设置画笔的颜色为白色。
fillcolor(“white”) 设置填充颜色为白色。
begin_fill() 开始填充图形。
n = int(input(“请输入科赫曲线的阶数：”)) 获取用户输入的科赫曲线的阶数。
for i in range(2): 循环两次，绘制两个连接的科赫曲线。
f(600, n) 绘制科赫曲线。
right(120) 右转角度为120度，用于绘制另外两个连接的科赫曲线。
end_fill() 结束图形的填充。
hideturtle() 隐藏海龟图标。
done() 完成整个绘图过程。

4.调用 main() 函数

main（）函数运行上述代码，并在控制台输入阶数，以绘制相应阶数的科赫曲线，并填充图形颜色。

5.效果：

三、举一反三

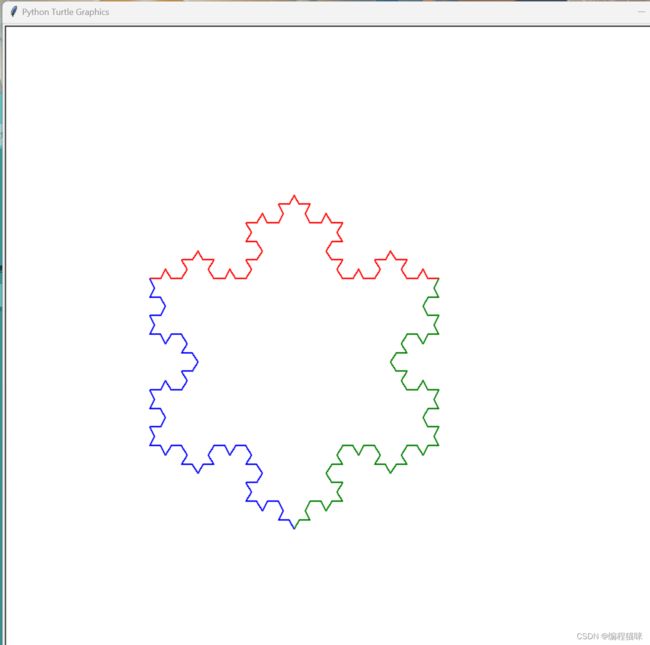
1. 改变雪花颜色：

from turtle import *

def f(size,n):
    if n == 0:
        fd(size) 
    else:
        for i in [0,60,-120,60]:
            left(i)
            f(size/3,n-1)
def main():
    setup(1000,1000)
    speed(0)
    penup()
    goto(-300,150)
    pensize(2)
    pendown()
    pencolor("red")
    f(400,3)
    right(120)
    pencolor("green")
    f(400,3)
    right(120)
    pencolor("blue")
    f(400,3)
    hideturtle()
    done()
main()

(可自行替换阶数)
绘制原理同上述内容

效果：

---

---

2. 反向绘制雪花，中间部分向下方绘制：
绘制时只需改变初始绘制角度

from turtle import *

def f(size,n):
    if n == 0:
        fd(size) 
    else:
        for i in [0,-60,120,-60]:
            left(i)
            f(size/3,n-1)
def main():
    setup(1000,1000)
    speed(0)
    penup()
    goto(-200,-150)
    pensize(2)
    pendown()
    pencolor("red")
    left(30)
    f(400,3)
    left(120)
    f(400,3)
    left(120)
    f(400,3)
    hideturtle()
    done()
main()

效果：

---

四、总结

科赫曲线是一种分形曲线，它通过重复迭代的方式构造出一条连续的曲线。

特点：

• 科赫曲线由一条线段开始，然后将每个线段分成三个等分，用等边三角形连接分割点。
• 通过不断迭代，每个线段都会被替换为一系列更小的线段，形成一个无限细分的曲线。
• 每次迭代过程中，曲线的长度都会增加三倍，而曲线的形状也会越来越接近于充满空间的曲线。

阶数：

• 科赫曲线的阶数决定了曲线细分的次数。阶数为0时，曲线只是一条直线；阶数为1时，曲线会分成四条线段；以此类推，阶数为n时，曲线会分成3^n条线段。

应用与变体：

• 科赫曲线广泛应用于数学教育中，用于展示和探索分形图形的概念。
• 科赫曲线有许多变体，如雪花曲线、雪花螺旋曲线、科赫岛、科赫曲线的填充等。

绘制科赫曲线的方法：

• 基于递归的方法是绘制科赫曲线最常用的方法。
• 绘制科赫曲线的基本思路是将当前线段分成三个等分，然后再以等边三角形连接分割点，并对每个子线段递归地应用相同的绘制规则。

科赫曲线是一个美丽而有趣的数学图形，展示了分形几何的奇妙特征。它在数学教育、计算机图形学和艺术创作等领域都有广泛的应用和研究。