AtCoder Beginner Contest 237题解（A-E)

AtCoder Beginner Contest 237题解

---

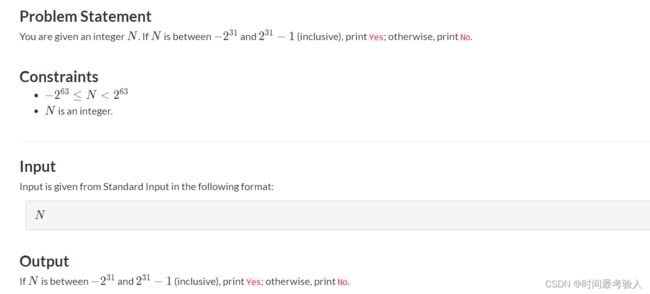
A - Not Overflow

【题目链接】A - Not Overflow (atcoder.jp)

题意：给一个数n，判断是否溢出！

两种解法：

• 计算2^31 - 1和-2^31，判断是否在范围内
• int类型的范围是-2^31 ~ 2^31-1，将LL型的n转为整型的m，如果两个数相等的话，说明没有溢出，反之溢出！
• 【代码实现】

#include
#include
#include
#include
#include

using namespace std;

typedef long long LL;

int main()
{
	LL n;
	cin >> n;
	if(n >= -pow(2,31) && n <= pow(2,31) - 1) puts("Yes");
	else puts("No");
	
	return 0;
}

【方法二】

#include
#include
#include
#include
#include

using namespace std;

typedef long long LL;

int main()
{
	LL n;
	cin >> n;
    
  	int m = n;
    
  	if(n == m) puts("Yes");
  	else puts("No");

	
	return 0;
}

B - Matrix Transposition

【题目链接】B - Matrix Transposition (atcoder.jp)

题意：求矩阵的转置。（将矩阵的行与列互换）

转置矩阵——百度百科

【直接转换】

#include
#include
#include
#include
#include

using namespace std;

typedef long long LL;


int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	int a[n][m], b[m][n];
	
	// 输入 
	for(int i = 0; i < n; i ++)
		for(int j = 0; j < m; j ++)
			scanf("%d", &a[i][j]);
	
	// 转换 
	for(int i = 0; i < m; i ++)
		for(int j = 0; j < n; j ++)
			b[i][j] = a[j][i];
	
	// 输出		
	for(int i = 0; i < m; i ++)
	{
		for(int j = 0; j < n; j ++)	printf("%d ", b[i][j]);
		puts("");
	}	
	
	return 0;
}

C - kasaka

【题目链接】C - kasaka (atcoder.jp)

题意：在一个字串串前加一些字符a，然后判断原串在操作之后能否形成回文串！

思路：处理两端的a，再满足可构成回文串条件下，然后再判断中间的串是否是回文串。

【代码实现】

#include
#include
#include
#include
#include

using namespace std;

//回文串判断（对称性） 
bool huiwen(string a)
{
	int len = a.size();
	bool flag = true;
	for(int i = 0; i <= len / 2; i ++)
	{
		if(a[i] != a[len - i - 1])
		{
			flag = false;
			break;
		}
	}
	if(flag) return true;
	else return false;
}
// 回文串的判断 

int main()
{
	string a;
	cin >> a;
	int len = a.size();

	//对两端的a进行处理，再判断中间的串是否为回文串
	int cnt1 = 0, cnt2 = 0, pos = len - 1;
	for(int i = 0; i < len; i ++)
	{
		if(a[i] != 'a') break;
		else cnt1 ++;
	}
	for(int i = len - 1; i >= 0; i --)
	{
		if(a[i] != 'a')
		{
			pos = i;
			break;
		 } 
		else cnt2 ++;	
	}

	//截取中间串 
	string b = a.substr(cnt1, len - cnt1 - cnt2 );//从某个位置开始， 长度为几的字串 

	 if(cnt1 == len)// 全a 
	 {
	 	puts("Yes");
	 	return 0; 
	 }
	 else if(cnt1 > cnt2) puts("No");// 怎么凑a都不可能 
	 else
	 {
	 	bool flag = true;
	 	if(huiwen(b))// 满足上面的情况，只要中间是回文一定能再拼a凑出回文 
	 	{
	 		flag = false;
		 }
		 if(flag) puts("No");
		 else puts("Yes");
	 }
	
	return 0;
}

D - LR insertion

【题目链接】D - LR insertion (atcoder.jp)

思路：双端队列，逆着过来实现。

• 碰到 ‘L’，我们从右边（队尾）插入数据。
• 碰到 ‘R’，我们从左边（队头）插入数据。

【回顾一下双端队列】

双端队列deque是一个支持在两端高效插入或删除元素的连续线性存储空间。它就像是vector和queue的结合。与vector相比，deque在头部增删元素仅需要O(1)的时间；与queue相比，deque像数组一样支持随机访问。

begin/end，返回deque的头/尾迭代器

front/back 队头/队尾元素

push_back从队尾入队

push_front从队头入队

pop_back从队尾出队

pop_front从队头出队

clear 清空队列

【代码实现】

#include
#include
#include
#include
#include
#include
#include 

using namespace std;

int main()
{
	deque<int> q;
	
	int n;
	cin >> n;
	string s;
	cin >> s;
	
	q.push_back(n);
	for(int i = n - 1; i >= 0; i --)
	{
		if(s[i] == 'L') 
			q.push_back(i);
		else
			q.push_front(i);	
	}
	for(auto &x : q) cout << x << ' ';

	return 0;
}

E - Skiing

【题目链接】E - Skiing (atcoder.jp)

题意：

题意：给定n个点和m条边以及这n个点的高度，对于从u点到v点，如果u点的高度大于等于v点的，则可以获得幸福值h[u]-h[v]，否者减少2 * (h[v] - h[u])的幸福值，求1号点出发能够获得的最大幸福值。

注：存在负值；双向连通；数据范围！

题解：

边的权值为两点的高度通过上述两种快乐值方式计算，可以将经过u->v获得的幸福值转化为u->v这条边的边权，这样这个问题就转化为从1出发能走的最长的路是多少，因为涉及到负权，因此迪杰斯特拉行不通，所以可以使用spfa来解决，计算出每个点到起点的最大开心值，最终取最大值即可！

【代码实现】

#include 
#include 
#include 
#include 
#include 


using namespace std;

typedef long long LL;

const int N = 1e6 + 10, M = N * 2;// 开大点！！ 
const LL INF = 0x3f3f3f3f;
int h[M], e[M], ne[M], idx;

int high[M];
LL  dist[M];
LL w[M];
bool st[M];
int n, m; 


void add(int a, int b, int c)  // 添加一条边a->b，边权为c
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

LL calc(int a, int b)
{
	
	if(high[a] > high[b])
		return high[a] - high[b];
	else 
		return 2 * (high[a] - high[b]);

}

void spfa()
{
	queue<int> q;
	
	//1. 初始化距离 : 负无穷 
	memset(dist, 128, sizeof dist);
	dist[1] = 0;
	
	q.push(1);
	st[1] = true;
	
	while(q.size())
	{
		auto t = q.front();
		q.pop();
		st[t] = false;
		
		for(int i = h[t]; i != -1; i = ne[i])
		{
			int j = e[i];
			if(dist[t] + w[i] > dist[j])
			{
				dist[j] = dist[t] + w[i];
				if(!st[j])
				{
					q.push(j);
					st[j] = true;	
				}	
			}	
		}	
	} 

}

int main()
{
	memset(h, -1, sizeof h);
	
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i ++) scanf("%d", &high[i]);
	
	while(m --)
	{
		int a, b;
		scanf("%d%d", &a, &b);
		if(a == b) continue;
		LL c = calc(a, b);// 计算a -->  b的边权
		LL c2 = calc(b, a);
		add(a, b, c); 
		add(b, a, c2);//无向边 
	}
	
	spfa(); 
	LL ans = -INF;
    for(int i = 1; i <= n; i ++)
    {
    	ans = max(ans, dist[i]);
    	
	}
	printf("%lld", ans);
	
    return 0;
}

注：如果文章有任何错误或不足，请各位大佬尽情指出，评论留言留下您宝贵的建议！如果这篇文章对你有些许帮助，希望可爱亲切的您点个赞推荐一手，非常感谢啦