9. 解谜游戏
目录
题目
Description
Input
Notes
思路
暴力方法
递归法
注意事项
C++代码(递归法)
关于DFS
题目
Description
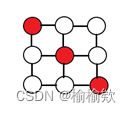
小张是一个密室逃脱爱好者,在密室逃脱的游戏中,你需要解开一系列谜题最终拿到出门的密码。现在小张需要打开一个藏有线索的箱子,但箱子上有下图所示的密码锁。
每个点是一个按钮,每个按钮里面有一个小灯。如上图,红色代表灯亮,白色代表灯灭。每当按下按钮,此按钮的灯以及其上下左右四个方向按钮的灯状态会改变(如果原来灯亮则灯灭,如果原来灯灭则灯亮)。如果小张通过按按钮将灯全部熄灭则能可以打开箱子。
对于这个密码锁,我们可以先按下左上角的按钮,密码锁状态变为下图。
再按下右下角的按钮,密码锁状态变为下图。
最后按下中间的按钮,灯全部熄灭。
现在小张给你一些密码锁的状态,请你告诉他最少按几次按钮能够把灯全部熄灭。
Input
第一行两个整数
![]()
接下来
![]()
行,每行一个长度为
![]()
的01字符串,0表示灯初始状态灭,1表示灯初始状态亮。
Output
一行一个整数,表示最少按几次按钮可以把灯全部熄灭。
Notes
第一个样例见题目描述,第二个样例按左上和右下两个按钮。
测试用例保证一定有解。
| 测试输入 | 期待的输出 | 时间限制 | 内存限制 | 额外进程 | |
|---|---|---|---|---|---|
| 测试用例 1 | 以文本方式显示
|
以文本方式显示
|
1秒 | 64M | 0 |
| 测试用例 2 | 以文本方式显示
|
以文本方式显示
|
1秒 | 64M | 0 |
思路
暴力方法
对每个灯点或不点分情况讨论,共讨论2^(n*m)次,超时了。
递归法
核心是深度优先搜索(DFS)。
1.用一个字符数组存各点的明暗情况,并且明确两点:
①一个灯至多按一次,按两次相当于没有按
②按的顺序对结果没有影响
2.如果第一排的点灯情况固定,那么后面n-1排的点灯情况也可固定;
因此我们可以枚举出第一排灯按与不按的所有情况,操作数为2^n;
自第二行开始到最后一行,通过判断上一行同一列的灯明灭与否来判断是否按灯;
最后需判断是否还有亮灯,如果有亮灯,则该枚举方法不合理;反之则记录点灯次数并与minPresses比较,更新minPresses值
注意事项
- minPresses的初始值为n*m,因为每个灯至多按一次,n*m为按灯的最大次数
- 用string来存取每一行的密码锁的状况,再遍历string将其存入二维数组
- 改变按钮状态时,注意不要越界
- 记得回溯。即在递归时,在按下当前按钮并进入下一次深搜后,要再次按下该按钮来复原。
- 用cal函数计算时,传入数组,而不是传入数组的地址。因为传入地址后,按灯时会改变原数组的情况且无法复原,这样就会影响下一次的计算。(最后卡了好久就是因为这个)
- 在递推完成之后要检验一下所有灯是否真的灭干净了,确认全部灯关掉之后再更新答案
- 解法不唯一,应该枚举第一排灯按与不按的所有情况,不断更新minPresses
C++代码(递归法)
#include
#include
#include
#include
using namespace std;
//按下按钮的函数
void pressButton(vector>&arr, int i, int j) {
arr[i][j] = 1 - arr[i][j];//改变当前按钮的状态
//改变上方按钮的状态
if (i > 0) {
arr[i - 1][j] = 1 - arr[i - 1][j];
}
//改变下方按钮的状态
if (i < int(arr.size()) - 1) {
arr[i + 1][j] = 1 - arr[i + 1][j];
}
//改变左方按钮的状态
if (j > 0) {
arr[i][j - 1] = 1 - arr[i][j - 1];
}
//改变右方按钮的状态
if (j < int(arr[0].size()) - 1) {
arr[i][j + 1] = 1 - arr[i][j + 1];
}
}
//计算按下的总次数
void cal(vector> arr, int curPresses, int& minPresses) {
for (int i = 1; i < int(arr.size()); i++) {
for (int j = 0; j >& arr, int col, int curPresses, int& minPresses) {
if (col == arr[0].size()) {
cal(arr, curPresses, minPresses);
return;
}
// 不按当前按钮
traverseFirstRow(arr, col + 1, curPresses, minPresses);
// 按当前按钮
pressButton(arr, 0, col);
traverseFirstRow(arr, col + 1, curPresses + 1, minPresses);
pressButton(arr, 0, col); // 恢复按钮当前状态
}
int main() {
int n, m;
cin >> n >> m;
int minPresses = n * m;
vector> arr(n, vector(m));
//读取密码锁的状态
for (int i = 0; i < n; i++) {
string row;
cin >> row;
for (int j = 0; j < m; j++){
arr[i][j]=row[j]-'0';
}
}
traverseFirstRow(arr, 0, 0,minPresses);
cout << minPresses << endl;
return 0;
} 关于DFS
DFS有一套固定的流程如下:
void dfs(状态参数)
{
if (达到中止条件 / 条件不合法)
{
添加相应内容
return;
}
for (下一步所有的可行方法)
{
标记;
dfs(参数进行相应改变);
还原标记;
}
}对于本道题目,dfs部分的伪代码可以参考如下:
void dfs(灯的id, 按键次数)
{
if (灯的id == m)
{
根据第一行状态推演所有按键次数;
判断所有灯是否全部熄灭;
更新最小按键次数;
return;
}
// 第一种:按下的情况
按下(第一行,第id个灯);
dfs(id + 1, 按键数 + 1);
按下(第一行,第id个灯); // 还原灯的状态
// 第二种:不按下的情况
dfs(id + 1, 按键数);
}