＜数据结构＞AVL树详解

目录

AVL是什么？

平衡因子

旋转

左单旋

右单旋

左右双旋

右左双旋

全部的代码

---

AVL树又叫平衡树(Balance_Tree)，笔者认为这个名字非常不错，中国嘛，就是在意阴阳平衡，之前小编还拿这个当过自己网络IP，哈哈哈。

AVL是什么？

本文适合有一点点数据结构基础的来看，简单的树形结构知道吧，也就是一堆根和结点的集合，那它有啥用呢？我们一般用树形结构来做什么呢？说这个之前，我们不妨先来看看其他的数据结构的作用

链表：它是链式结构，单向和双向两种结构，能做到简单的数据插入和删除，且效率不算低，时间复杂度 O(1)，查找数据时间复杂度 O(N)

栈：满足先入后出的特性，不支持查找

队列：满足先入先出的特性，不支持查找

顺序表：线性表结构，能做到简单的插入删除，效率相比链表低了些，时间复杂度O (N)，查找数据的时间复杂度 O(N)

上面列举的几个结构，我们将其相互对比一下，最理想的也就是插入可以O(1)，但是查找是O(N)，那如果我们还想要再优化呢，这里大家去了解一下二叉搜索树，很简单的一个用于数据搜索的树形结构，它的插入是O(1)，数据查询是有条件达到O(logN)的，但是由于没有任何的优化算法，所以搜索树可能会出现左右子树的高度差太大了，甚至数据都在一边的极端情况，这时的查找复杂度又变为了O(N)，我们这里介绍的AVL树就是在二叉搜索树的基础上进行了优化调整，结果是控制每一个根结点的左右子树的高度差不超过1

上面说所的高度差不超过1，也是AVL树的平衡由来

平衡因子

为了便于我们控制平衡的算法，我们引入一个平衡因子 bf 进来，并制定规则：新插入的结点在左子树 bf--，在右结点 bf++

template
struct AVLTreeNode
{
	// 三叉链
	AVLTreeNode* _left;
	AVLTreeNode* _right;
	AVLTreeNode* _parent;

	std::pair _kv; // 数据
	int _bf; // 平衡因子

	AVLTreeNode(const pair& kv)
		:_left(nullptr),
		_right(nullptr),
		_parent(nullptr),
		_kv(kv),
		_bf(0)
	{

	}
};

这样我们可以直接通过平衡因子的数值来反映该结点是否已经平衡了。AVL树要保证的就是每一棵子树都是平衡的，最后总体也就平衡了。如果 bf == 0 说明左右子树高度相等，bf == 1 说明右子树比左子树高一层，bf == -1 说明左子树比右子树高一层，否则其他情况都是不符合平衡的

说到这，最重要的接口就是Insert插入接口的设计了

平衡树的数据都是(K，V)结构的，我们采用pair来放有效数据，我们将需要的数据传入接口时，我们第一步要做的就是找到我们待插入的位置，延续搜索二叉树的特点，为了方便后面left就是左子树，right就是右子树，root就是根结点，parent就是父节点

规定：left < root < right

直接和传入的kv值比较查询即可

		while (cur)
		{
			// 找到待插入叶子 规定：left < root < right
			parent = cur;
			if (cur->_kv.first < kv.first)
			{
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

找到后在判断该位置是parent的left还是right插入即可

// 找到后开始插入
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		cur->_parent = parent;

正常插入后，便是关键的一步，更新控制平衡因子！

就和上面说的一样，从插入这里的parent开始逐步向上更新，插入的是left就是parent->_bf--，right就是++，之后在判断 parent->_bf 的值，如下

如果 bf == 0 说明左右子树高度相等，bf == 1 说明右子树比左子树高一层，bf == -1 说明左子树比右子树高一层，否则其他情况都是不符合平衡的，则需要做旋转的处理，下面的函数我们后续详细解释，这个是精髓！！！

// 更新平衡因子
        while (parent)
		{
			if (cur == parent->_right)
			{
				parent->_bf++;
			}
			else if (cur == parent->_left)
			{
				parent->_bf--;
			}

			if (parent->_bf == 0)
			{
				break;
			}
			else if (abs(parent->_bf) == 1)
			{
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (abs(parent->_bf) == 2)
			{
				// 说明parent所在的子树已经不平衡了，需要旋转处理
				if (parent->_bf == 2 && cur->_bf == 1) // 左单旋
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1) // 右单旋
				{
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1) // 左右旋转
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1) // 右左旋转
				{
					RotateRL(parent);
				}
				else
				{
					assert(false);
				}

				break;
			}
			else
			{
				// 树出问题了
				assert(false);
			}
		}

上面代码的框架就完成了80%了，剩下的就只需要将其20%的旋转细节处理完就可以了，这里看到有左旋，右旋，左右旋转，右左旋转，是什么意思呢？我们看下图

 我们看到左边的cur插入后，8结点的 bf == 2了，不满足平衡了，我们做了一次旋转处理后，在不改变 left < root < right 这个条件的前提下，又让了 left 和 right 的高度差 == 0 了，这就是一次旋转处理，接下来我们只需要将所有的旋转情况完善即可。

旋转

左单旋

 左单旋处理的情况，图中见，parent的右子树的右子树插入结点后破坏了平衡，我们进行一次左单旋后，变成右边的样子，重新恢复平衡，左旋含义即将这里的30从左边上旋转到了左下来。

void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* pNode = parent->_parent;

		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}

		parent->_parent = subR;
		subR->_left = parent;
		
		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			subR->_parent = pNode;

			if (parent == pNode->_left)
			{
				pNode->_left = subR;
			}
			else
			{
				pNode->_right = subR;
			}
		}

		subR->_bf = parent->_bf = 0;
	}

右单旋

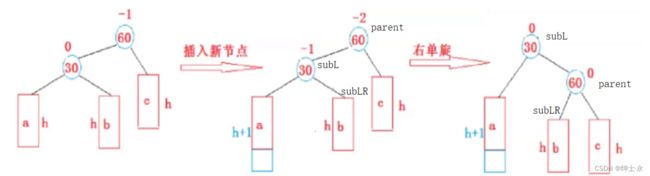
和上面的左单旋情况类似

 右单旋的含义就是右上的60旋转到右下来了

void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* pNode = parent->_parent;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}

		parent->_parent = subL;
		subL->_right = parent;

		if (_root == parent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			subL->_parent = pNode;
			if (pNode->_left == parent)
			{
				pNode->_left = subL;
			}
			else
			{
				pNode->_right = subL;
			}
		}

		subL->_bf = parent->_bf = 0;
	}

左右双旋

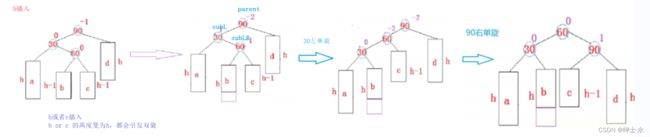
 这里的情况稍微复杂了一点，左单旋和右单旋都是处理的要么是右边的增加，要么是左边的增加，双旋处理的是中间子树增加，这里中间子树的增加又可以分为两种情况，加在左子树和加在右子树

从这里的图中看出，现在处理的事加在左子树的情况，注意这里的左右子树是90结点的左右子树，图中也可以看出，60结点插入在它的left和right的处理情况相同，唯一的差别就是处理后，需要区别的处理一下平衡因子的更新

甚至我们可以想一个极端情况，下面看到依然是不影响的

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		RotateL(subL);
		RotateR(parent);

		// 左子树 or 右子树
		if (bf == -1)
		{
			subL->_bf = 0;
			parent->_bf = 1;
		}
		else if (bf == 1)
		{
			subL->_bf = -1;
			parent->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
		}
		else
		{
			assert(false);
		}
		subLR->_bf = 0;
	}

右左双旋

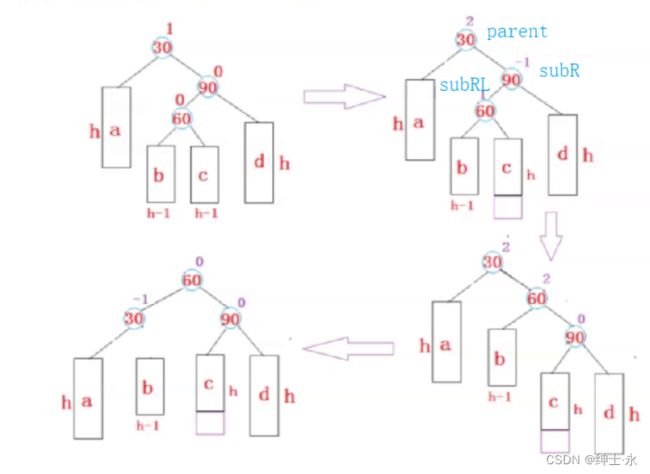
和左右双旋类似，这里新结点是插入在了parent的右边中间

 我们根据图中的结构变化来处理结点之间的关系即可，先将90右旋，再将30左旋

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
			
		RotateR(subR);
		RotateL(parent);

		// 左子树 or 右子树
		if (bf == -1)
		{
			subR->_bf = 1;
			parent->_bf = 0;
		}
		else if (bf == 1)
		{
			subR->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
		}
		else
		{
			assert(false);
		}
		subRL->_bf = 0;
	}

全部的代码

#pragma once

#include 
#include