<高阶数据结构>图
图
- 必要概念
-
- 大致用途
- 存图
-
- 邻接矩阵
- 邻接表
- 遍历
-
- BFS(广度优先)
- DFS(深度优先)
- 最小生成树
-
- Kruskal算法
- Prim算法
- 寻最短路径
-
- Dijkstra算法
必要概念
图根据有无方向分为,有向图和无向图
组成:G = (V, E)
- 顶点集合 V
- 边的集合 E
G(Graph),V(Vertex),E(Edge)
图可以说是一个灰常抽象且学习比较有挑战性的一个数据结构,一个图是由顶点集合和边集合组成的
大致用途
- 表示交通网络图,例如,顶点是城市,边是城市之间的距离
- 表示社交关系图
存图
一般存储我们有两种方法
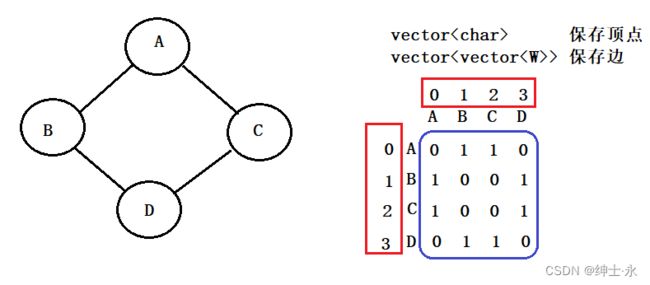
邻接矩阵
优点:
- 非常适合存储稠密图
- O(1)判断两个顶点的连接关系,并取得权值
缺点:
- 相对而言不适合用来查找一个顶点连接的所有边O(N)
template
class Graph
{
public:
Graph(const V* a, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(a[i]);
_indexMap[a[i]] = i;
}
_matrix.resize(n);
for (size_t i = 0; i < _matrix.size(); ++i)
{
_matrix[i].resize(n, MAX_W);
}
}
// 获取顶点映射下标
size_t GetVertexIndex(const V& v)
{
auto it = _indexMap.find(v);
if (it != _indexMap.end())
{
return it->second;
}
else
{
//assert(false);
throw std::invalid_argument("顶点不存在");
return -1;
}
}
void _AddEdge(size_t srci, size_t dsti, const W& w)
{
// 无向图
if (Direction == false)
{
_matrix[srci][dsti] = w;
_matrix[dsti][srci] = w;
}
else
{
_matrix[srci][dsti] = w;
}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_AddEdge(srci, dsti, w);
}
}
void Print()
{
// 打印顶点
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
}
cout << endl;
cout << " ";
for (size_t i = 0; i < _matrix.size(); ++i)
{
//cout << i << " ";
printf("%-4d", i);
}
cout << endl;
// 打印矩阵
for (size_t i = 0; i < _matrix.size(); ++i)
{
cout << i << " "; // 竖下标
for (size_t j = 0; j < _matrix.size(); ++j)
{
//cout << _matrix[i][j] << " ";
if (_matrix[i][j] == MAX_W)
{
//cout << "* ";
printf("%-4c", '*');
}
else
{
//cout << _matrix[i][j] << " ";
printf("%-4d", _matrix[i][j]);
}
}
cout << endl;
}
cout << endl;
}
}
private:
std::vector _vertexs; // 顶点集合
std::map _indexMap; // 顶点对应的下标关系
std::vector> _matrix; // 邻接矩阵
};
邻接表
- 使用vector保存所有的顶点
- 使用链表保存与每个顶点连通的顶点
优点:
- 适合存储稀疏图
- 适合查找一个顶点连接的边
缺点:
- 不适合去确定两个顶点是否相连及权值
namespace link_table
{
template
struct Edge
{
int _dsti; // 目标点的下标
W _w; // 权值
Edge* _next;
Edge(int dsti, const W& w)
:_dsti(dsti)
,_w(w)
,_next(nullptr)
{
}
};
template
class Graph
{
typedef Edge Edge;
public:
// 图的创建
// 1.IO输入 -- 不方便测试 OJ适合
// 2.图结构关系写到文件,读取文件
// 3.手动添加边 -- 方便测试修改
Graph(const V* a, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(a[i]);
_indexMap[a[i]] = i;
}
_tables.resize(n, nullptr);
}
size_t GetVertexIndex(const V& v)
{
auto it = _indexMap.find(v);
if (it != _indexMap.end())
{
return it->second;
}
else
{
//assert(false);
throw std::invalid_argument("顶点不存在");
return -1;
}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
// 1->2
Edge* eg = new Edge(dsti, w);
eg->_next = _tables[srci];
_tables[srci] = eg;
// 如果是无向图 2->1
if (Direction == false)
{
Edge* eg = new Edge(srci, w);
eg->_next = _tables[dsti];
_tables[dsti] = eg;
}
}
}
void Print()
{
// 打印顶点
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
}
cout << endl;
for (size_t i = 0; i < _tables.size(); ++i)
{
cout << _vertexs[i] << "[" << i << "]->";
Edge* cur = _tables[i];
while (cur)
{
cout << _vertexs[cur->_dsti] << "[" << cur->_dsti << " : " << cur->_w << "]" << "->";
cur = cur->_next;
}
cout << "nullptr" << endl;
}
}
private:
std::vector _vertexs; // 顶点集合
std::map _indexMap; // 顶点对应的下标关系
std::vector _tables; // 邻接表
};
void TestGraph1()
{
Graph g("0123", 4);
g.AddEdge('0', '1', 1);
g.AddEdge('0', '3', 4);
g.AddEdge('1', '3', 2);
g.AddEdge('1', '2', 9);
g.AddEdge('2', '3', 8);
g.AddEdge('2', '1', 5);
g.AddEdge('2', '0', 3);
g.AddEdge('3', '2', 6);
g.Print();
}
}
遍历
BFS(广度优先)
以某一顶点为起点,一层一层的向外遍历

我们只需借助一个队列来辅助实现,这里我们先将A入队列,在A出队列的时候,将A连通的最近一层B,C,D入队列,B出队列时将E入队列,如此运行直到队列为空时,遍历结束,出队列顺序即时我们的遍历次序
为了防止B出队列时,再次将A和C入队列,可以开一个标记容器,标记入了队列的顶点
void BFS(const V& src)
{
size_t srci = GetVertexIndex(src);
// 队列和标记数组
std::queue q;
std::vector visited(_vertexs.size(), false);
q.push(srci);
visited[srci] = true;
int levelSize = 1;
while (!q.empty())
{
// 一层一层出
for (size_t i = 0; i < levelSize; ++i)
{
int front = q.front();
q.pop();
cout << front << ":" << _vertexs[front] << " ";
// 把front的邻接顶点入队列
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (_matrix[front][i] != MAX_W)
{
if (visited[i] != true)
{
q.push(i);
visited[i] = true;
}
}
}
cout << endl;
}
levelSize = q.size();
}
cout << endl;
}
DFS(深度优先)
void _DFS(size_t srci, std::vector& visited)
{
cout << srci << ":" << _vertexs[srci] << endl;
visited[srci] = true;
// 找一个srci相邻的没有访问过的点,去往深度遍历
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (_matrix[srci][i] != MAX_W && visited[i] == false)
{
_DFS(i, visited);
}
}
}
void DFS(const V& src)
{
size_t srci = GetVertexIndex(src);
std::vector visited(_vertexs.size(), false);
_DFS(srci, visited);
}
最小生成树
- 构成生成树这些边加起来权值是最小的
这里采用两种算法,两种算法都采取了贪心的策略
Kruskal算法
方法
每次找权值最小边,注意这个最小边不能构成环,将所有顶点连接起来结束算法
可以借助一个并查集结构,用于判断已选的边是否构成环
这个算法是看的局部最优边,只关注局部最优
下图是算法笔记这本书里面的算法流程图

定义个Edge边结构,辅助算法
struct Edge
{
size_t _srci;
size_t _dsti;
W _w;
Edge(size_t srci, size_t dsti, const W& w)
:_srci(srci)
, _dsti(dsti)
, _w(w)
{
}
bool operator>(const Edge& e) const
{
return _w > e._w;
}
};
W Kruskal(Self& minTree)
{
// 初始化minTree
size_t n = _matrix.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (size_t i = 0; i < n; ++i)
{
minTree._matrix[i].resize(n, MAX_W);
}
std::priority_queue, std::greater> minque;
for (size_t i = 0; i < _matrix.size(); ++i)
{
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (j > i && _matrix[i][j] != MAX_W)
{
minque.push(Edge(i, j, _matrix[i][j]));
}
}
}
//选出n-1条边
W totalw = 0;
int size = 0;
UnionFindSet ufs(_matrix.size());
while (!minque.empty())
{
Edge eg = minque.top();
minque.pop();
if (!ufs.InSet(eg._srci, eg._dsti))
{
cout << _vertexs[eg._srci] << "->" << _vertexs[eg._dsti] << endl;
minTree._AddEdge(eg._srci, eg._dsti, eg._w);
ufs.Union(eg._srci, eg._dsti);
++size;
totalw += eg._w;
}
}
if (size == n - 1)
return totalw;
else
return -1;
}
Prim算法
方法
从某一顶点开始,选择该顶点连接的边中权值最小的边,再到下一顶点选连接的边中最小权值的边,同样需要记录一下已经选过了的顶点
借助一个队列实现,和广度优先遍历方法有点类似,只不过这里只需要选择最小权值边的顶点
int Prim(Self& minTree, const V& src)
{
size_t srci = GetVertexIndex(src);
size_t n = _vertexs.size();
// 初始化minTree
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (size_t i = 0; i < n; ++i)
{
minTree._matrix[i].resize(n, MAX_W);
}
vector visited(n, false);
std::priority_queue < Edge, std::vector, std::greater> pq;
for (size_t i = 0; i < n; ++i)
{
if (_matrix[srci][i] != MAX_W)
{
pq.push(Edge(srci, i, _matrix[srci][i]));
}
}
size_t size = 0;
visited[srci] = true;
int total = 0;
while (!pq.empty())
{
Edge front = pq.top();
pq.pop();
if (visited[front._dsti] == true)
{
continue;
}
cout << _vertexs[front._srci] << "->" << _vertexs[front._dsti] << endl;
minTree._AddEdge(front._srci, front._dsti, front._w);
if (size == n -1)
{
break;
}
// 入队列
for (size_t i = 0; i < n; ++i)
{
if (visited[i] != true && _matrix[front._dsti][i] != MAX_W)
{
pq.push(Edge(front._dsti, i, _matrix[front._dsti][i]));
}
}
++size;
total += front._w;
visited[front._dsti] = true;
}
return total;
}
寻最短路径
找某个顶点到图中另一顶点走的最短路径
Dijkstra算法
使用的也是贪心的策略
- 将选择了的顶点和没有选择的顶点分为两个集合
- dist记录从s顶点到Q顶点的最短路径权值和
- pPath记录满足最短路径时每个顶点的上一个顶点下标
- 定义一个S数组记录已经确定的最短顶点,一旦选定不可更改
下图
- 起始,s到s的最短路径权值和为0,dist[0]=0,上一个顶点为s下标为0,pPath[0]=0
- s起点,s到y的最短路径权值和为5. dist[1]=5,pPath[1]=0,s到t的最短路径权值和为10,dist[3]=10,pPath[3]=0
- 选权值最小的y作为起点,s通过y到t的最短路径权值和为8. 8 < 10, 更新dist[3]=8,pPath[3]=1,s通过y到x最短路径权值和为14,dist[4]=14,pPath[4]=1, ,s通过y到z最短路径权值和为7,dist[2]=7,pPath[4]=1,
void PrintShortPath(const V& src, const vector& dist, const vector& parentPath)
{
size_t N = _vertexs.size();
size_t srci = GetVertexIndex(src);
for (size_t i = 0; i < N; ++i)
{
if (i == srci)
continue;
vector path;
int parenti = i;
while (parenti != srci)
{
path.push_back(parenti);
parenti = parentPath[parenti];
}
path.push_back(srci);
reverse(path.begin(), path.end());
for (auto pos : path)
{
cout << _vertexs[pos] << "->";
}
cout << dist[i] << endl;
}
}
void Dijkstra(const V& src, vector& dist, vector& pPath)
{
size_t srci = GetVertexIndex(src);
size_t n = _vertexs.size();
dist.resize(n, MAX_W);
pPath.resize(n, -1);
dist[srci] = W();
pPath[srci] = 0;
vector s(n, false);
for (size_t i = 0; i < n; ++i)
{
W min = MAX_W;
size_t u = srci;
for (size_t j = 0; j < n; ++j)
{
if (s[j] != true && dist[j] < min)
{
min = dist[j];
u = j;
}
}
// 松弛算法
for (size_t k = 0; k < n; ++k)
{
if (s[u] == false && _matrix[u][k] != MAX_W
&& dist[u] + _matrix[u][k] < dist[k])
{
dist[k] = dist[u] + _matrix[u][k];
pPath[k] = u;
}
}
s[u] = true;
}
}