【C++初阶】stack的常见操作和模拟实现

个人主页：@Weraphael
✍作者简介：目前学习C++和算法
✈️专栏：C++航路
希望大家多多支持，咱一起进步！
如果文章对你有帮助的话
欢迎 评论 点赞 收藏 加关注✨

---

一、stack

1.1 stack的基本概念

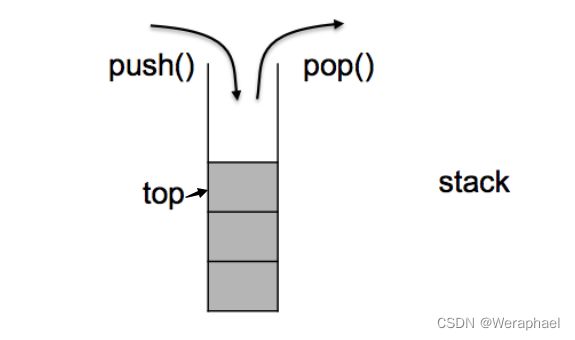
• stack是一种容器适配器（通过容器转化出来的），是一种先进后出(First in Last Out，简称FILO)，它只有一个出口。
• 容器适配器是一种特殊的容器，它们通过某种方式改变了底层容器的接口或行为。常见的容器适配器还有队列queue和优先队列priority_queue。
• 注意：容器适配器通常会限制对底层容器的访问方式，只有栈顶的元素才能被使用，因此不能有遍历的行为（底层没有设计迭代器）。例如栈和队列都是限制在一端插入或删除元素，优先队列则通过堆来维护元素的有序性。

1.2 stack的常见操作

1.2.1 常见构造函数

• 无参的默认构造（构造空的栈）

// T可以是任意类型
stack<T> _st;

• 拷贝构造

// _st已知
stack<T> _st(s);

1.2.2 push

功能：将元素val压入stack中

1.2.3 pop

功能：将stack中尾部的元素弹出

1.2.4 empty

功能：判断stack是否为空，如果为空则返回真，反之。

1.2.5 top

功能：返回栈顶元素

1.2.6 size

功能：返回stack中元素的个数

1.2.7 栈的遍历

既然栈不支持迭代器，只能打印栈顶的元素，然后出栈。重复以上操作直到栈为空

【代码示例】

#include 
#include 
using namespace std;

int main()
{
    stack<int> _st;
    _st.push(1);
    _st.push(2);
    _st.push(3);
    _st.push(4);

    while (!_st.empty())
    {
        cout << _st.top() << ' ';
        _st.pop();
    }
    cout << endl;

    return 0;
}

【输出结果】

二、有关栈的力扣经典题

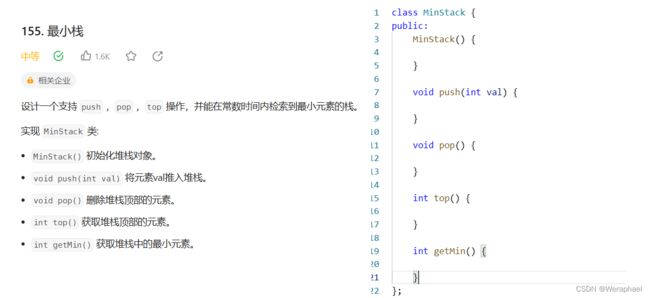
2.1 最小栈

题目链接：点击跳转

【题目描述】

【思路】

可以定义两个栈，一个栈_st可以用于出栈和入栈操作，另一个栈_min_st用于更新当前_st出栈和入栈的最小值。

对于入栈接口：_st正常入栈。如果_min_st为空，则入栈的值val和_st一样；如果不为空，则要比较_min_st当前栈顶的元素是否大于或者等于_st的栈顶元素，如果大于或等于则要入栈。

对于出栈接口：首先要分析_st的栈顶元素是否等于_min_st的栈顶元素，如果相等则要出栈，而_st无论如何都要出栈。

最后，_min_st的栈顶元素则是最小元素的栈。

【代码实现】

class MinStack {
public:
    MinStack() 
    {}
    // 自定义类型会调用默认构造函数
    // 因此可以不用写
    
    void push(int val) 
    {
        _st.push(val);
        if (min_st.empty() || val <= min_st.top())
        {
            min_st.push(val);
        }
    }
    
    void pop() 
    {
        if (_st.top() == min_st.top())
        {
            min_st.pop();
        }
        _st.pop();
    }
    
    int top() 
    {
        return _st.top();
    }
    
    int getMin() 
    {
        return min_st.top();
    }

private:
    stack<int> _st; 
    stack<int> min_st;
};

2.2 栈的压入、弹出序列

题目链接：点击跳转

【题目描述】

【思路】

这题直接模拟就行了。

首先定义一个栈_st，并且分别定义变量i和j来遍历pushV数组和popV数组，接下来让pushV里的元素一个一个入栈(i++)，然后再判定栈顶元素是否等于popV下标为j的元素，如果相等则要出栈。最后如果栈为空，说明栈popV是是pushV弹出的顺序。

要注意pushV可能为空

【代码实现】

class Solution {
public:
    bool IsPopOrder(vector<int>& pushV, vector<int>& popV) 
    {
        stack<int> _st;
        int i = 0; // 遍历pushV
        int j = 0; // 遍历popV
        while (i < pushV.size())
        {
            // 入栈
            _st.push(pushV[i]);
            i++;

            while (!_st.empty() && _st.top() == popV[j])
            {
                _st.pop();
                j++;
            }
        }
        // 如果栈为空，说明匹配
        return _st.empty();
    }
};

2.3 逆波兰表达式求值

题目链接：点击跳转

【题目描述】

【思路】

首先来解释什么是逆波兰表达式求值，逆波兰表达式求值又称后缀表达式，而我们常见的是中缀表达式，例如2 + 1 * 3化成后缀表达式2 1 3 * +

因此我们的思路是：
设计一个栈_st，如果遇到操作数，则将操作数入栈；如果遇到运算符（本题的操作符只有+ - * /），则将两个操作数出栈，但是要注意操作数的顺序，先出栈的是右操作数，出栈后的下一个栈顶元素则是左操作数，对于加法和乘法来说操作数的顺序是无关紧要的，但是对于减法和除法，操作数就要有讲究了。

最后计算出的值继续入栈，直到遍历完毕之后，栈内只有一个元素，则该元素（也就是栈顶）为逆波兰表达式的值。

注意要将string类字符串转化成整型计算，string转化成整型有个函数：atoi

【代码实现】

class Solution {
public:
    int evalRPN(vector<string>& tokens) 
    {
        stack<int> _st;
       
        for (auto& x : tokens)
        {
            if (x != "+" && x != "-" && x != "*" && x != "/")
            {
            	// 如果不为操作符就入栈
                _st.push(stoi(x));
            }
            else
            {
                int right = _st.top();
                _st.pop();
                int left = _st.top();
                _st.pop();
				
				// 计算
                switch(x[0])
                {
                case '+':
                    _st.push(left + right);
                    break;
                case '-':
                    _st.push(left - right);
                    break;
                case '*':
                    _st.push(left * right);
                    break;
                case '/':
                    _st.push(left / right);
                    break;
                }
            }
        }
        return _st.top();
    }
};

2.4 用栈实现队列

题目链接：点击跳转

【题目描述】

【思路】

举一组数据：1、2、3、4。如果是出栈的话，第一个出的数据是4，而现在要用栈来模拟队列，第一个出的数据必须是1。所以一开先将4个数据全部入栈（push），然后一个个出栈到另一个栈（pop）中，这样1就在栈顶了，对于栈的性质，靠近栈顶的元素先出，这样就能实现栈模拟队列了。

【动图展示】

【代码实现】

class MyQueue {
public:
    MyQueue() {}
    
    void push(int x) 
    {
        _st.push(x);
    }
    
    int pop() 
    {
        if (_queue.empty())
        {
            while (!_st.empty())
            {
                int val = _st.top();
                _st.pop();
                _queue.push(val);
            }
        }
        int front_val = _queue.top();
        _queue.pop();
        return front_val;
    }
    
    int peek() 
    {
        if (_queue.empty())
        {
            while (!_st.empty())
            {
                int val = _st.top();
                _st.pop();
                _queue.push(val);
            }
        }
        return _queue.top();
    }
    
    bool empty() 
    {
        return _queue.empty() && _st.empty();
    }
    
private:
    stack<int> _st;
    stack<int> _queue;
};

三、模拟实现stack

3.1 简介

stack是一种容器适配器，容器适配器可以被视为一种包装器，它们通过修改底层容器的接口或行为来实现新的功能。通过使用这些容器适配器，开发者可以方便地在不同场景下使用已有容器的功能，并且无需关心底层容器的具体实现。

其实就是STL中封装好的栈，在使用的时候我们不仅可以指定内部的数据类型，还可以指定内部的容器。不指定容器其实也是可以的，模板参数有一个缺省值，默认是deque

int main()
{
	//内部容器为vector
	stack<int, vector<int>> s1;  
	
	//内部容器为list   
	stack<int, list<int>> s2; 
	
	//内部为默认容器deque      
    stack<int> s3;      
                
	return 0;
}

3.2 代码实现

注意：指定内部的容器需要有push_back、pop_back、back、size、empty等函数接口

#pragma once

namespace wj
{
	template<class T, class container = deque<T>>
	class stack
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_back();
		}

		T& top()
		{
			return _con.back();
		}

		size_t size()
		{
			return _con.size();
		}

		bool empty()
		{
			return _con.empty();
		}

	private:
		container _con;
	};
}

【测试代码】

#include 
#include 
using namespace std;
#include "stack.h"
int main()
{
	wj::stack<int> _st;
	_st.push(1);
	_st.push(2);
	_st.push(3);
	_st.push(4);

	while (!_st.empty())
	{
		cout << _st.top() << ' ';
		_st.pop();
	}
	cout << endl;
	cout << "个数为：" << _st.size() << endl;
	return 0;
}

【输出结果】