李沐-动手学习深度学习（预备知识）

仅作为学习笔记，推荐去原网站看原版！！！

预备知识

2.1. 数据操作 — 动手学深度学习 2.0.0 documentation (d2l.ai)

首先介绍n维数组，也就是张量（tensor），所有的深度学习框架，它的张量类（比如TensorFlow中的Tensor）都与Numpy中的ndarray类似，但不同的是，深度学习框架会比ndarray多一些重要功能：

• GPU很好地支持加速计算，NumPy仅仅支持CPU计算
• 张量类支持自动微分，使得张量类更加适合深度学习

数据操作

入门

深度学习的环境，如果电脑的配置不太好的话，建议直接去kaggle上白嫖（学习应该是够用了哈哈哈哈哈）

Kaggle：Kaggle: Your Home for Data Science

本节的目标是帮助读者了解并运行一些在阅读的过程中会用到的基本数值计算工具。

首先导入torch（虽然被叫做PyTorch，但是代码中是使用的是torch）

import torch

张量可以表示成一个由数值组成的数组，这个数组可能有多个维度。具有一个轴的张量对应数学中的向量，具有两个轴的张量对应数学中的矩阵，两个轴以上的在数学中就没有特殊的名称了。

x=torch.arange(12)
x
#tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

可以通过张量的shape属性来访问张量（沿每个轴的长度）的形状 。

x.shape
#torch.Size([12])

如果只想知道张量中元素的总数，即形状的所有元素乘积，可以检查它的大小（size）。 因为这里在处理的是一个向量，所以它的shape与它的size相同。

x.numel()
#12

要想改变一个张量的形状，可以调用reshape函数。 例如，可以把张量x从形状为（12,）的行向量转换为形状为（3,4）的矩阵。

这个新的张量包含与转换前相同的值，但是它被看成一个3行4列的矩阵。 要重点说明一下，虽然张量的形状发生了改变，但其元素值并没有变。 注意，通过改变张量的形状，张量的大小不会改变。

x=x.reshape(3,4)
x
#tensor([[ 0,  1,  2,  3],
#        [ 4,  5,  6,  7],
#        [ 8,  9, 10, 11]])

可以从上面看到，一个（12，）的行向量就转化成了（3，4）的矩阵。

但是我们也可以不需要通过手动指定每个维度来改变形状，比如：如果我们的目标形状是（高度，宽度），那么我们在知道宽度以后，也就能够知道高度是多少，用上一个例子，加入要获得一个宽度为4的矩阵（可以直接计算出，高度为3，但是如果维度大了就不好计算了），我们可以通过-1来调节自动计算出维度的功能。比如x.reshape(-1,4)或者x.reshape(3,-1)

有时候，我们希望使用全0、全1、其他常量，或者从特定分布中随机采样的数字来初始化矩阵。 比如：我们可以创建一个形状为（2,3,4）的张量，其中所有元素都设置为0。

x = torch.zeros((2,3,4))
#如果要是全1，则用torch.ones(2,3,4)
x
#tensor([[[0., 0., 0., 0.],
#         [0., 0., 0., 0.],
#         [0., 0., 0., 0.]],

#        [[0., 0., 0., 0.],
#         [0., 0., 0., 0.],
#         [0., 0., 0., 0.]]])

有时我们想通过从某个特定的概率分布中随机采样来得到张量中每个元素的值。 例如，当我们构造数组来作为神经网络中的参数时，我们通常会随机初始化参数的值。
下面的代码创建一个形状为（3,4）的张量。 其中的每个元素都从均值为0、标准差为1的标准高斯分布（正态分布）中随机采样。

x = torch.randn(3,4)
x
#tensor([[-0.2361,  1.6423,  1.6631,  0.7491],
#        [-1.5840, -0.8781,  0.8213, -2.8956],
#        [-0.7808, -1.6647, -0.2332, -0.9112]])

我们还可以通过提供包含数值的Python列表（或嵌套列表），来为所需张量中的每个元素赋予确定值。 在这里，最外层的列表对应于轴0，内层的列表对应于轴1。

torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
#tensor([[2, 1, 4, 3],
#        [1, 2, 3, 4],
#        [4, 3, 2, 1]])

运算符

如果我们要在数据上执行一些数学操作，最简单也是最有用的就是按照元素（elementwise）进行运算。它们将标准标量运算符应用于数组的每个元素。 对于将两个数组作为输入的函数，按元素运算将二元运算符应用于两个数组中的每对位置对应的元素。 我们可以基于任何从标量到标量的函数来创建按元素函数。

在数学表示法中，我们将通过符号$f:R\to R$来表示一元标量运算符（只接收一个输入）。 这意味着该函数从任何实数（$R$）映射到另一个实数。 同样，我们通过符号$f:R,R\to R$表示二元标量运算符，这意味着该函数接收两个输入，并产生一个输出。 给定同一形状的任意两个向量$u$和$v$和二元运算符$f$， 我们可以得到向量$c=F(u,v)$。 具体计算方法是$ci\leftarrow f(ui,vi)$， 其中$ci、ui$和$vi$分别是向量$c、u$和$v$中的元素。 在这里，我们通过将标量函数升级为按元素向量运算来生成向量值 $F:Rd,Rd\to Rd$。

具有相同形状的张量，常见的标准运算符（+、-、*、/和**）可以升级称为按照元素运算，比如

x = torch.tensor([1, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y  # **运算符是求幂运算
#(tensor([ 3.,  4.,  6., 10.]),
# tensor([-1.,  0.,  2.,  6.]),
# tensor([ 2.,  4.,  8., 16.]),
# tensor([0.5000, 1.0000, 2.0000, 4.0000]),
# tensor([ 1.,  4., 16., 64.]))

#还有像求幂这样的一元运算
torch.exp(x)
#tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])

当然除了这些，还可以进行线性代数运算，包括向量点积和矩阵乘积（线性代数那一部分讲）

同时我们还可以把多个张量连结起来（concentrate），把它们端对端地叠起来形成一个更大的张量。我们只需要提供张量列表，并给出沿哪个轴连结（联想pandas的concat）。

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
#(tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [ 2.,  1.,  4.,  3.],
#         [ 1.,  2.,  3.,  4.],
#         [ 4.,  3.,  2.,  1.]]),
# tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],
#         [ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],
#         [ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]]))

当我们沿行（轴-0，形状的第一个元素） 和按列（轴-1，形状的第二个元素）连结两个矩阵时，会发生什么情况。 我们可以看到，第一个输出张量的轴-0长度（6）是两个输入张量轴-0长度的总和（3+3）； 第二个输出张量的轴-1长度（8）是两个输入张量轴-1长度的总和（4+4）。

还有可以通过逻辑运算符构建二元张量，比如X==Y：

X
#tensor([[ 0.,  1.,  2.,  3.],
#        [ 4.,  5.,  6.,  7.],
#        [ 8.,  9., 10., 11.]])

Y
#tensor([[2., 1., 4., 3.],
#        [1., 2., 3., 4.],
#        [4., 3., 2., 1.]])

X == Y
#tensor([[False,  True, False,  True],
#        [False, False, False, False],
#        [False, False, False, False]])

还可以利用sum对所有元素求和

X.sum()
#tensor(66.)

广播机制

除了对相同形状张量的数据操作，还可以对不同形状张量，我们仍然可以进行数据操作（广播机制），广播机制的工作方式：

1. 通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状。
2. 对生成的数组执行按元素操作

大多数情况是沿着数组中长度为1的轴进行广播。

a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b
#(tensor([[0],
#         [1],
#         [2]]),
# tensor([[0, 1]]))

查看一下a、b的shape，可以看到a的shape是$3\ast 1$，b的shape是$1\ast 2$

让二者相加就是将a往右复制一列，让b往下复制3行，让其均变为$3\ast 2$的形式

a+b
#tensor([[0, 1],
#        [1, 2],
#        [2, 3]])

索引和切片

就像在任何其他Python数组中一样，张量中的元素可以通过索引访问。 与任何Python数组一样：第一个元素的索引是0，最后一个元素索引是-1； 可以指定范围以包含第一个元素和最后一个之前的元素。

X[-1], X[1:3]
#(tensor([ 8.,  9., 10., 11.]),
# tensor([[ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.]]))
#还可以在指定位置上修改元素
X[1, 2] = 9
X
#tensor([[ 0.,  1.,  2.,  3.],
#        [ 4.,  5.,  9.,  7.],
#        [ 8.,  9., 10., 11.]])

如果我们想为多个元素赋值相同的值，我们只需要索引所有元素，然后为它们赋值。 例如，[0:2, :]访问第1行和第2行，其中“:”代表沿轴1（列）的所有元素。 虽然我们讨论的是矩阵的索引，但这也适用于向量和超过2个维度的张量。

X[0:2, :] = 12
X
#tensor([[12., 12., 12., 12.],
#        [12., 12., 12., 12.],
#        [ 8.,  9., 10., 11.]])

节省内存

（初学者或许不用太在意？？）

运行一些操作可能会导致为新结果分配内存。 例如，如果我们用Y = X + Y，我们将取消引用Y指向的张量，而是指向新分配的内存处的张量。这可能是不可取的，原因有两个：

1. 首先，我们不想总是不必要地分配内存。在机器学习中，我们可能有数百兆的参数，并且在一秒内多次更新所有参数。通常情况下，我们希望原地执行这些更新；
2. 如果我们不原地更新，其他引用仍然会指向旧的内存位置，这样我们的某些代码可能会无意中引用旧的参数。

幸运的是，执行原地操作非常简单。 我们可以使用切片表示法将操作的结果分配给先前分配的数组，例如：

Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))
#id(Z): 139878472632944
#id(Z): 139878472632944

#如果在后续计算中没有重复使用X， 我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。
before = id(X)
X += Y
id(X) == before
#True

转化为其他python对象

将深度学习框架定义的张量转换为NumPy张量（ndarray）很容易，反之也同样容易。 torch张量和numpy数组将共享它们的底层内存，就地操作更改一个张量也会同时更改另一个张量。

A = X.numpy()
B = torch.tensor(A)
type(A), type(B)
#(numpy.ndarray, torch.Tensor)

#要将大小为1的张量转换为Python标量，我们可以调用item函数或Python的内置函数。
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
#(tensor([3.5000]), 3.5, 3.5, 3)

小结

深度学习存储和操作数据的主要接口是张量（n维数组）

练习

• 运行本节中的代码。将本节中的条件语句X == Y更改为X < Y或X > Y，然后看看你可以得到什么样的张量。

X < Y
#tensor([[ True, False,  True, False],
#        [False, False, False, False],
#        [False, False, False, False]])

X > Y
#tensor([[False, False, False, False],
#        [ True,  True,  True,  True],
#        [ True,  True,  True,  True]])

• 用其他形状（例如三维张量）替换广播机制中按元素操作的两个张量。结果是否与预期相同？

a = torch.arange(12).reshape((2,2, 3))
b = torch.arange(6).reshape((1, 3,2))
a+b

运行上述代码会出现报错The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 2

网友给出的回答是：

由于广播原则的限制，从直观上也可以理解，扩展的时候无法确定是按照2中的哪个元素复制，所以不可以进行。

网友总结的广播原则：

维度按照右对齐后，需要复制的维度只有一行/列或者为空，其余行/列不需要复制。

这个可以复制成功，因为需要复制的维度全部是1
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a+b

可以复制成功，因为右对齐后第一个维度为空，且要复制的维度为1
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((2))
a+b

这个无法复制，因为要复制的有两列
a = torch.arange(18).reshape((3,6))
b = torch.arange(6).reshape((3,2))
a+b

这种可以复制，因为只有一行需要复制
a = torch.arange(18).reshape((3,6))
b = torch.arange(6).reshape((1,6))
a+b

这种不能复制，因为第一维需要复制的有两行

a = torch.arange(12).reshape((2,2,3))
b = torch.arange(12).reshape((6,2,1))
a+b

数据预处理

接触过机器学习的可以跳过！！！

主要介绍的就是利用pandas预处理原始数据，并将原始数据转换为张量格式的步骤。感兴趣的可以尝试polars进行数据处理，会发现一片新大陆！！（但是入门比较麻烦。）

转化为张量格式

将pandas处理后的数据转化为张量形式，由于没有数据集，所以就直接copy书上的代码了。

import torch

X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, y

#(tensor([[3., 1., 0.],
#         [2., 0., 1.],
#         [4., 0., 1.],
#         [3., 0., 1.]], dtype=torch.float64),
# tensor([127500, 106000, 178100, 140000]))

小结

• pandas软件包是Python中常用的数据分析工具中，pandas可以与张量兼容。
• 用pandas处理缺失的数据时，我们可根据情况选择用插值法和删除法。

练习

创建包含更多行和列的原始数据集。

懒得创建了，所以选择了一个比赛的数据集。但是操作都是一样的。

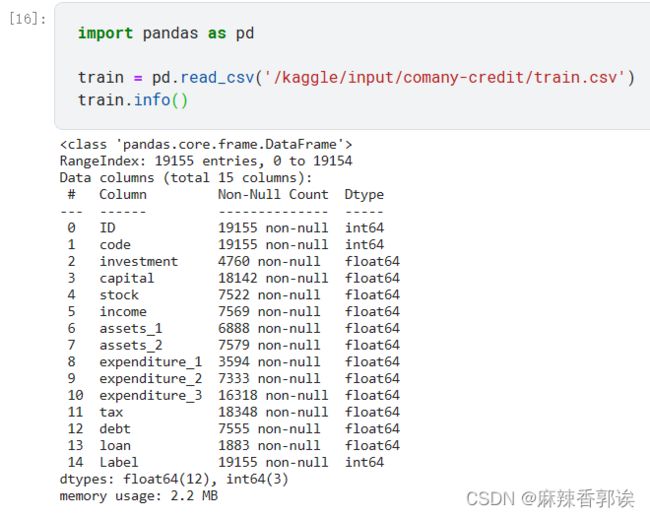
1. 删除缺失值最多的列。

   可以从输出信息看出，缺失值最多的是loan这一个属性列。利用下列代码删除它。

   train = train.drop('loan',axis=1)
   train.info()
   
   

或者用如下代码也能有一样的效果：

# 计算每列中缺失值的数量
missing_values = train.isna().sum()
# 找到具有最大值的列的名称，并删除该列
train = train.drop(missing_values.idxmax(), axis=1)
train.info()

首先，我们可以使用 isna() 函数和 sum() 函数来计算每列中缺失值的数量。isna() 用于检查 DataFrame 中每个元素是否为缺失值，返回一个由 True/False 值组成的 DataFrame，然后 sum() 函数用于计算每列中 True 值的数量（即缺失值的数量）。

接下来，我们可以使用 idxmax() 函数来查找具有最大值的列的名称。idxmax() 函数返回最大值所在的索引（即列名称），我们可以将其作为参数传递给 drop() 函数，从而删除该列。

2. 将预处理后的数据集转换为张量格式。

线性代数

书中说这部分内容能够帮助读者了解和实现本书介绍的大多数模型。主要介绍基本数学对象，算术和运算，并用数学符号和代码实现。

标量

数字之间的加减乘除可以被看作是一些基本的线性代数。严格来说，仅包含一个数值被称为标量（scalar）。例如：$c=\frac{5}{9}(f-32)$中5、9、32都是标量值，符号c和f都被称为变量（variable），它们表示未知的变量值。

在这本书中，标量变量都由小写字符表示。用$R$表示所有（连续）实数标量的空间,$x\in R$是表示x是一个实值标量的正式形式。

标量由只有一个元素的张量表示。下面的代码实例化了两个标量，执行加乘除和指数运算。

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x * y, x / y, x**y
#(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))

向量

向量可以被看作是标量值组成的列表，里面的标量就是元素或者分量。当数据集中的数据用向量表示的时候，这时候向量里面的标量也就有了具体的含义。比如一张二维表，有以下属性：

ID
code
investment
capital
stock
income
assets_1
assets_2
expenditure_1
expenditure_2
expenditure_3
tax
debt
loan
Label

这时候每一行对应的某一列都有其具体的含义。比如第一行、第一列就是第一个用户的ID，以此类推。在数学中向量通常都是通过加粗的小写符号表示。

通过一维张量表示向量，一般来讲，张量具有任意长度，取决于机器的内存限。

x = torch.arange(4)
x
#tensor([0, 1, 2, 3])

我们可以用下标来引用向量的任一元素，比如$x_i$表示第i个元素。注意，这里的$x_i$表示一个具体的值，是一个标量。所以不会加粗。

向量$x$可以表示为：
x = [ x 1 x 2 x 3 ⋅ ⋅ ⋅ x n ] x=\begin{bmatrix} x_1\\ x_2 \\ x_3 \\ ···\\ x_n \end{bmatrix} x= ​x1​x2​x3​⋅⋅⋅xn​​ ​
这里面的$x_i$就是元素，可以通过所以来访问，比如$x[1]$就是访问的$x_1$

长度、维度和形状

向量只是一个数字数组，就像每个数组都有一个长度一样，每个向量也是如此。 在数学表示法中，如果我们想说一个向量x由n个实值标量组成， 可以将其表示为$x\in R^n$。 向量的长度通常称为向量的维度（dimension）。

注： 向量或轴的维度被用来表示向量或轴的长度，即向量或轴的元素数量。 然而，张量的维度用来表示张量具有的轴数。 在这个意义上，张量的某个轴的维数就是这个轴的长度

我们可以用下标来引用向量的任一元素，比如$x_i$表示第i个元素。注意，这里的$x_i$表示一个具体的值，是一个标量。所以不会加粗。

向量$x$可以表示为：
x = [ x 1 x 2 x 3 ⋅ ⋅ ⋅ x n ] x=\begin{bmatrix} x_1\\ x_2 \\ x_3 \\ ···\\ x_n \end{bmatrix} x= ​x1​x2​x3​⋅⋅⋅xn​​ ​
这里面的$x_i$就是元素，可以通过所以来访问，比如$x[1]$就是访问的$x_1$

长度、维度和形状

向量只是一个数字数组，就像每个数组都有一个长度一样，每个向量也是如此。 在数学表示法中，如果我们想说一个向量x由n个实值标量组成， 可以将其表示为$x\in R^n$。 向量的长度通常称为向量的维度（dimension）。

注： 向量或轴的维度被用来表示向量或轴的长度，即向量或轴的元素数量。 然而，张量的维度用来表示张量具有的轴数。 在这个意义上，张量的某个轴的维数就是这个轴的长度

矩阵

巴拉巴拉…………没空写了，大家没看过的自己去看一遍趴哈哈哈哈哈哈哈哈哈哈