决策树（CLS, ID3, CART, 随机森林, 参数详解），一篇就够了

概况与基本概念

概况

原则：判断的越快越好，决策树尽量不要太深，保证好的泛化能力，同时又保证训练集上准确率；
特点：可读性，分类速度快；
可表示为IfThen形式；
可认为定义在特征空间与类空间上条件概率分布；
过程依赖于属性变量取值特点；
可自动判断属性变量重要性，忽略不重要属性变量；

主要算法：CLS, ID3, C4.5, CART

CLS算法

CLS Concept Learning System:
思想：选择属性，根据属性值划分子集；
原则：（1） 如果子集为空或属于同一类，为叶结点；
（2）否则，对应于内部结点，即测试结点；
（3）选择新属性进行划分，直至得到条件（1）
问题：没有指定选择属性原则，方法及先后顺序，而选择的顺序对学习比较有影响。

ID3算法

熵，信息增益

Iterative Dichotomiser3 迭代二叉树3
改进算法，解决了属性选择问题
思想： 使用信息增益选择测试属性；
插入 信息增益概念：
信息量：对事件不确定性的度量，越是不均匀分布，比如0,1分布，p越接近1，概率越大，不确定性越小；
或者对事件均匀分布的度量，越是均匀分布，比如p=0.5, 信息量越大，不确定性越大；
引入熵：信息量大小的度量，表示不确定性，熵越大，不确定性越大；
对于取有限个值得随机变量，概率分布为：
$$P(X=x_i)=p_i,i=1,2,...,n$$
X的熵定义为：$$H(X)=-\sum _{i=1}^n{p}_i\log p_i$$
可见熵只依赖于X的分布，和X的具体取值无关
熵越大，随机变量不确定性越大：
$$0\le H(p)\le \log n$$
右侧等号，当且仅当$$p_i=\frac{1}{n}$$
也就是均匀分布时，熵最大，也就是平均信息量最大。

引入 条件熵：
设随机变量（X,Y）,联合概率分布：
$$P(X=x_i,Y=y_i)=p_{ij}$$
$$i=1,2,...,n;j=1,2,...,m$$
条件熵H(Y|X)：在已知随机变量X的条件下随机变量Y的不确定性，即X给定条件下Y的条件概率分布的熵对X的数学期望：
$$H(Y\mid X)=\sum _{i=1}^n{p}_{i}H(Y\mid X=x_i)$$

如果以上熵和条件熵，是由数据估计（如极大似然估计）得到时，所对应熵和条件熵为经验熵empirical entropy和经验条件熵empirical conditional entropy

引入 信息增益Information gain：特征A对训练数据集D的信息增益g(D,A), 定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即
$$g(D,A)=H(D)-H(D\mid A)$$
对于g(Y,X)表示： 得知特征X使得Y的信息不确定性减少的程度。显然，g(Y,X)越大，表示该特征X对于确定Y贡献越大，具有更强更有效的分类能力，也就是我们需要优先考虑的特征。从而可作为选择特征的参照。
也称互信息mutual information。

以下ID3算法：
符号表示：
$$\mid D\mid :样本容量、样本个数$$
$$K个类：C_k,k=1,2,...K$$
$$\mid C_k\mid 为属于类C_k的样本个数$$
$$设特征A有n个不同取值a_1,a_2,...a_n$$
$$根据A的取值将D划分为n个子集D_1,...,D_n$$
$$\mid D_i\mid 为D_i的样本个数$$
$$D_{ik}为子集D_i中属于C_k的样本集合$$
$$\mid D_{ik}\mid 为D_{ik}的样本个数$$

计算方法：
输入： 数据集D和特征A；
输出： 特征A对D的信息增益g(D,A)

1. 计算数据集D的经验熵H(D):
   $$H(D)=-\sum _{k=1}^K\frac{\mid C_k\mid }{\mid D\mid }{\log }_2\frac{\mid C_k\mid }{\mid D\mid }$$
2. 计算特征A对数据集D的经验条件熵H(D\midA)
   $$H(D\mid A)=\sum _{i=1}^n\frac{\mid D_i\mid }{\mid D\mid }H(D_i)=-\sum _{i=1}^n\frac{\mid D_i\mid }{\mid D\mid }\sum _{k=1}^K\frac{\mid D_{ik}\mid }{\mid D_i\mid }{\log }_2\frac{\mid D_{ik}\mid }{\mid D_i\mid }$$
3. 计算信息增益
   $$g(D,A)=H(D)-H(D\mid A)$$

ID3决策树生成

依次计算各特征的信息增益选最大作为根结点；
产生新的结点，继续根据信息增益选下一个属性；以此类推。

数据准备：Data cleaning
删除减少噪音：data normalization
数据归纳：generalize data to higher level concepts using concept hierarchies
信息标准化：data normalization.

尽量控制每个属性可能值不超过7种（最好不超过5种）

关联性分析Relevance analysis: 对于与问题无关的属性删除；删除对属性可能值大于7且不能归纳的属性

ID3基本思想： ID3 以信息熵为度量，用于决策树结点的属性选择，每次优选信息量最多的属性（条件信息熵最小，信息增益最大），构造一个熵值下降最快的决策树，直到叶子结点处熵值为0.此时叶子结点对应实例为同一类。

问题： 采用信息增益划分训练数据集时，偏向于选取取值较多的（n大的）特征或属性问题，但这些特征可能是无意义的特征，如用户ID，学号，日期等。如果选取值较多的特征，会使决策树分支过多。

所以引入信息增益比information gain ratio $g_R(D,A)$：特征A对训练数据集D的信息增益比定义为其信息增益g(D,A)与训练数据D关于特征A的值的熵$H_A(D)$之比：
$$g_R(D,A)=\frac{g(D,A)}{H_A(D)}$$
$$H_A(D)=-\sum _{i=1}^n\frac{\mid D_i\mid }{\mid D\mid }{\log }_2\frac{\mid D_i\mid }{\mid D\mid }$$

$H_A(D)$ 可看作对信息增益的惩罚参数，特征A取值越多，$H_A(D)$越大，倾向于去减小$g_R(D,A)$，从而一定程度客服信息增益偏向于取n较大的特征的问题。

理想的决策树：
（1）叶子结点数最少；
（2）叶子结点深度最小；
（3）叶子结点数最少且叶子结点深度最小；

另一个问题：决策树会增长树的每个分支深度，直到恰好能对训练样本集比较完美的分类。但实际中，若数据中有噪声或训练样例数量太少，不能产生目标函数的有代表性的采样时，会遇到困难。

ID3决策树剪枝

防止过拟合，进行减枝，pruning
减枝Pruning: 从已生成的树上裁掉一些子树或叶子结点，将其根结点或父节点作为新的叶节点，从而简化模型；

逆向：通过极小化决策树整体损失函数或代价函数来实现；
决策树学习损失函数：
$$C_{\alpha }(T)=C(T)+\alpha \mid T\mid =\sum _{t=1}^{\mid T\mid }{N}_t{H}_t(T)+\alpha \mid T\mid$$
$$H_t(T)=-\sum _k\frac{N_{tk}}{N_t}\log \frac{N_{tk}}{N_t}$$
$$C(T)=\sum _{t=1}^{\mid T\mid }{N}_t{H}_t(T)=-\sum _{t=1}^{\mid T\mid }\sum _{k=1}^K{N}_{tk}\log \frac{N_{tk}}{N_t}$$
$H_t(T)$: 叶节点t上的经验熵，$\alpha \ge 0$为参数
$\mid T\mid$: 叶节点个数
$t:$: 树T的叶节点
$N_t$: 该叶节点样本数
$N_{tk}$: $N_t$中k类的样本数，$k=1,2,...K$

剪枝算法具体如下：
输入：生成算法产生的整个树$T$, 参数$\alpha$
输出：修剪后的子树$T_{\alpha }$
(1) 计算每个节点的经验熵；
(2) 递归地从树的叶节点向上回缩，判断：如果叶子结点回缩到父节点之前$T_B$和之后$T_A$的树的损失函数满足：
$$C_{\alpha }(T_A)\le C_{\alpha }(T_B)$$
则进行剪枝；
(3) 返回（2），直到不能继续，得到损失函数最小的子树。

以上均是解决分类任务的ID3。接下来介绍既可以回归又可以分类的CART。

CART算法

CART算法，Classification and Regression Trees
目标变量是类别——分类树
目标变量是连续——回归树

CART特点：
（1）是二元划分，二叉树不易产生数据碎片，精确度高于多叉树；
数据碎片data fragmentation：由于大多数决策树算法采用自顶向下递归划分方法，沿着树向下，记录会越来越少，在叶节点，记录可能太少，对于叶节点代表的类，不能做出具有统计意义的判决，就是所谓的数据碎片问题。解决问题一种可行方法是，当样本小于某个特定阈值时，停止分裂

（2）可根据不同变量，选择多种指标;
分类目标： Gini指数，熵
连续目标： 最小平方残差、最小绝对残差

（3）剪枝：用预剪枝或后剪枝对训练集生成树进行剪枝；

（4）树的建立：若目标变量标称，且有两个以上类别，则会考虑把目标类别合并成两个超类（双化）；若目标变量连续，则CART算法会找出一组基于树的回归方程来预测目标变量；

CART 回归树

假设Y是连续变量，给定训练数据集：
$D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$

假设已将输入空间划分为M个单元$R_1,R_2,...,R_m$, 并且每个单元$R_m$上有一个固定的输出$c_m$, 回归树表示为：
$$f(x)=\sum _{m=1}^M{c}_{m}I(x\in R_m)$$

用平方误差来表示预测误差，用平方误差最小准则求每个单元最优输出值：
$$\sum _{x_i\in R_m}(y_i-f(x_i){)}^2$$
$R_m$上的C_m的最优值：
$${\hat{c}}_m=ave(y_i\mid x_i\in R_m)$$

那么问题来了：以上是怎么划分的输入空间，得到$R_1,R_2,...R_m$的呢？

启发式：
(1) 选择$x$的第$j$个分量$x^{(j)}$和它的值$s$, 作为切分变量和切分点，形成两个区域：
$$R_1(j,s)=\{x\mid x^{(j)}\le s\}和R_2(j,s)=\{x\mid x^{(j)}>s\}$$

(2) 然后通过下式寻找最优切分变量和切分点：
$$\underset{j,s}{\min }(\underset{c_1}{\min }\sum _{x_i\in R_1(j,s)}(y_i-c_1{)}^2+\underset{c_2}{\min }\sum _{x_i\in R_2(j,s)}(y_i-c_2{)}^2)$$

解释：
固定输入特征$j$，可通过式子先求出最优切分点$s$，求出${\hat{c}}_1$ 和 ${\hat{c}}_2$:
$${\hat{c}}_1=ave(y_i\mid x_i\in R_1(j,s))$$
$${\hat{c}}_2=ave(y_i\mid x_i\in R_2(j,s))$$

遍历所有特征$j$, 从而可得到最优的$j$
(3) 对两个区域重复上述划分，直到满足停止条件。得到最小二乘回归树。

CART 分类树

引入基尼指数Gini Index:
分类问题中，设有$k$个类，样本点属于$k$的概率为$P_k$, 则概率分布的基尼指数：
$$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$

对于二分类问题：$Gini(p)=2p(1-p)$

对于样本集合D，基尼指数：
$$Gini(D)=1-\sum _{k=1}^K(\frac{\mid C_k\mid }{\mid D\mid }{)}^2$$

若样本集合D根据特征A是否为a被分割为D1和D2， 即
$$D_1=\{(x,y)\in D\mid A(x)=a\},D_2=D-D_1$$

则在特征A条件下，集合D的基尼指数：
$$Gini(D,A)=\frac{\mid D_1\mid }{\mid D\mid }Gini(D1)+\frac{\mid D_2\mid }{\mid D\mid }Gini(D_2)$$

基尼指数和熵都可近似代表分类误差率。

CART生成算法：
输入： 训练数据集D， 停止计算条件
输出：CART决策树

从根结点开始，递归地对每个节点操作：

1. 设结点数据集D，对每个特征A，对其每个值，根据样本点对$A=a$ 的测试为是或否，将$D$分成$D_1$和$D_2$, 计算$A=a$的基尼指数；
2. 在所有特征A以及所有可能切分点a中，选择基尼指数最小的特征和切分点，将数据集分配到两个子节点中；
3. 对两个子节点递归调用1,2
4. 生成CART树

CART剪枝算法

1. 从生成算法产生的决策树T_0底端开始不断剪枝，直到T_0的根结点，形成子树序列$\{T_0,T_1,...T_n\}$;
2. 通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树；

具体步骤：

1. 剪枝，形成子树序列： 计算子树损失函数,
   $$C_{\alpha }(T)=C(T)+\alpha \mid T\mid$$
   对固定的$\alpha$， 一定存在损失函数最小的子树，记为$T_{\alpha }$, 当$\alpha$ 变大时，最优子树$T_{\alpha }$倾向于减小，当$\alpha =0$时，整体树最优，$\alpha$ 趋近无穷大，单节点最优。

Breiman 等人证明，可以用递归方法对树进行剪枝，将$\alpha$从小增大， $0={\alpha }_0<{\alpha }_1<{\alpha }_2<...<{\alpha }_n<+\infty$
产生一系列的区间$[{\alpha }_i,{\alpha }_{i+1})$
以上$n+1$个区间 $\alpha \in [{\alpha }_0,{\alpha }_1),...[{\alpha }_n,\infty )$ ，最优子树序列$T_0,T_1,...T_n$

具体如下：

(1) 首先要理解，所谓剪枝，是减掉某些叶结点，返回到其根结点（父结点），即返回到某内部结点，以下将遍历所有内部结点，计算分析，在什么样的情况下剪枝该内部结点下面的子树。

对于某一内部结点（理解为生成树后，还未曾剪枝的所有内部结点中的某一个，不失普遍性），既可以看作单结点，也可以看作以其为根结点形成的子树的父节点，不同角度损失函数计算也不同：

若看作单结点$t$(即相当于其下的子结点均被剪枝，相当于剪枝后)的损失函数：
$$C_{\alpha }（t）=C(t)+\alpha$$
若看作以$t$为根结点的子树$T_t$(相当于未被剪枝，保留其子结点，剪枝前)的损失函数：
$$C_{\alpha }(T_t)=C(T_t)+\alpha \mid T_t\mid$$

当$\alpha =0$或接近$0$，很小时,相当于基本不考虑树结构复杂度的影响，则有
$$C_{\alpha }(T_t)<C_{\alpha }(t)$$

逐渐增大$\alpha$, 即逐渐增加树结构复杂度对于损失函数的权重，必有一$\alpha$, 使：
$$C_{\alpha }(T_t)=C_{\alpha }(t)$$
$$\alpha =\frac{C(t)-C(T_t)}{\mid T_t\mid -1}$$

当$\alpha$增大到此值时，是否剪此枝，都有相同的损失函数，而剪枝后结点更少，所以剪枝$T_t$。

以上计算过程其实给了我们一个判断标准，对任一个内部结点，都可以定义其属性：
$$g(t)=\frac{C(t)-C(T_t)}{\mid T_t\mid -1}$$

我们比较当前$\alpha$ 和 所有内部结点的$g(t)$：
当$\alpha <g(t),等价C_{\alpha }(T_t)<C_{\alpha }(t)$, 不对$t$剪枝；
当$\alpha \ge g(t),等价C_{\alpha }(T_t)\ge C_{\alpha }(t)$, 对$t$ 剪枝；

序列得到方法：

从$T_0$, 计算所有内部结点$t$的属性$g(t)$， 并将其从小到大排列，得到$g(t)$ 序列；

在$T_0$中，剪去$g(t)$最小的$T_t$, 使其变为叶节点$t$, 得到树作为$T_1$, 记${\alpha }_1=g(t)$；

在$T_1$中，剪去$g(t)$最小的$T_t$, 使其变为叶节点$t$, 得到树作为$T_2$, 记${\alpha }_2=g(t)$；

…
在$T_i$中，剪去$g(t)$最小的$T_t$, 使其变为叶节点$t$, 得到树作为$T_{i+1}$, 记${\alpha }_{i+1}=g(t)$；
…

在$T_{n-1}$中，剪去$g(t)$最小的$T_t$, 使其变为叶节点$t$, 得到树作为$T_n$, 记${\alpha }_n=g(t)$；设此时，$T_n$已变为单结点树。

则有：
$T_0$ 为区间 $\alpha \in [{\alpha }_0,{\alpha }_1)$ 内的最优树；

$T_1$ 为区间 $\alpha \in [{\alpha }_1,{\alpha }_1)$ 内的最优树；

…

$T_n$ 为区间 $\alpha \in [{\alpha }_n,\infty )$ 内的最优树；

以上较为详尽地介绍了子树序列生成方法，接下来选取最优子树；

(2) 在剪枝得到的子树序列$\{T_0,T_1,...T_n\}$中通过交叉验证选取最优子树$T_{\alpha i}$ （${\alpha }_i\in \{0,1,2...,n\}$）：

利用独立的验证数据集，测试子树序列中各子树的平方误差或基尼指数，最小的决策树就是最优决策树。

当$T_{\alpha i}$ 确定时， $\alpha \in [{\alpha }_i,{\alpha }_{i+1})$随之确定。

完成剪枝。

随机森林RF

概念（引入Bootstrap/Bagging/RF）

2001年，Breiman 把分类树组合成随机森林。
Random Forest, 其中的Random 指：
（1）训练样本选择方面的Random: Bootstrap 方法随机选择样本；
（2）特征选择方面的Random: 属性中随机选择k个属性，每个树节点分裂时，从这随机的k个属性里，选择最优的。

引入Bootstrap概念：
本意指高靴子口后面的悬挂物，穿靴子时用手向上拉的工具，Bootstraping 指’Pull up by your own bootstraps’ 即 ‘通过拉靴子让自己上升’， 意思指‘不可能发生的事’，后来意思发生转变，隐喻“不需要外界帮助，仅靠自身理论让自己变得更好”。

引入Bagging 策略， Bootstrap aggregation:
从样本中重采样（有重复的）选出n个样本，在所有属性上，对此n个样本建立分类器（ID3，C4.5, CART, SVM， Logistic回归等），重复以上两步m次，获得m个分类器，将数据放在这m个分类器上，最后根据这m个分类器的投票结果，决定数据属于哪一类。

随机森林在Bagging基础上做了修改（主要是在属性选择上，不是所有属性，而是随机数量的属性feature）：

RF流程

流程：
（1） 原始训练集为$N$, 应用Bootstrap 法有放回地 随机抽取$k$个新的自助样本集，并由此构建$k$棵分类树，每次未被抽到的样本组成$k$个袋外数据；

（2） 设有$m_{all}$个属性，则随机抽取$m_{try}$个属性作为每棵树的分支依据，然后在每个结点从$m_{try}$中选择最优分类能力的属性，进行分支；

（3）每棵树最大限度地生长，不做任何修剪；

（4）将生成的多棵分类树组成随机森林，用随机森林分类器对新的数据进行判别和分类，分类结果按树分类器的投票多少而定。

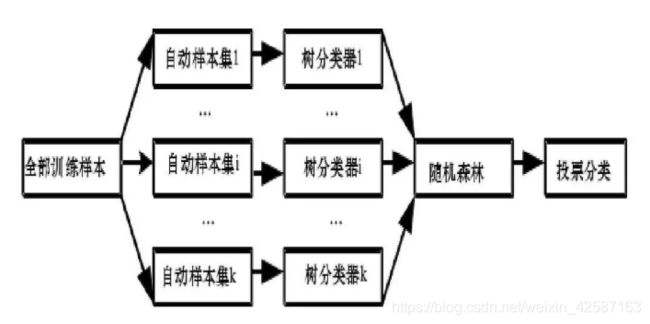
运算量没有显著提高前提下提高了预测精度。

RF特点

优点：
（1） 两个随机性的引入，使随机森林不容易陷入过拟合，因为选择样本时就不是全部样本；
（2） 两个随机性的引入，使随机森林具有很好抗噪声能力；
（3） 能处理很高维度(feature很多)的数据，并且不用做特征选择，可以处理成千上万的输入变量，并确定最重要的变量，因此被认为是不错的降维方法；
（4）对数据集适应能力强：既能处理离散型（如ID3, CART），也能处理连续型（如C4.5, CART），数据集无需规范化；
（5） 可生成一个Proximities 邻近矩阵$=(p_{ij})$, 用于度量样本间的相似性：
$$p_{ij}=\frac{a_{ij}}{N}$$
$a_{ij}$：表示样本$i$和$j$出现在随机森林中同一个叶子结点的次数；
$N$：表示随机森林中树的棵数
（6）能够有效地运行在大数据上；
（7）对于缺省值问题，能获得很好的结果。

缺点：
（1）解决回归问题时，没有像在分类中表现的好，因为其并不能实际给出一个连续型的输出。进行回归时，随机森林不能做出超越训练集数据范围的预测，可能导致在对某些还有特定噪声的数据建模时出现过拟合；
（2）对于统计建模者来说，随机森林更像一个黑盒子，无法控制内部运行，只能在不同参数和随机种子之间进行尝试。

RF如何选Feature 数量

随机森林分类效果（错误率）与两个因素有关：
（1）森林中任意两棵树的相关性：相关性越大，错误率越大；
（2）森林中每棵树的分类能力：每棵树分类能力越强，整个森林错误率越低。

随机森林比较重要的参数Feature数量$m_{try}$, 存在一对矛盾：
减少特征选择个数$m_{try}$, 树的相关性和分类能力也会相应降低；
增大$m_{try}$, 树的相关性和分类能力随之增大。

袋外错误率：
如何选择最优的$m_{try}$， 主要依据是计算袋外错误率oob-error(out of bag error)。

随机森林有一重要优点是，没有必要对它进行交叉验证或者用独立测试集来获得误差的一个无偏估计，因为它可以用袋外数据在内部进行自行评估，也就是说在生成过程中就可以对误差建立一个无偏估计。

上面知道，生成每棵树时，对训练集用了不同的bootstrap sample(随机有放回地抽取)，因此对每棵树，均有一部分数据，没有参与其生成，它们成为该树的oob样本，即袋外样本数据。

这样的采样特点允许我们进行obb估计，计算方式如下：
（1）对每个样本，计算它作为oob样本的树对它的分类情况；
（2）以简单多数投票作为该样本的分类结果；
（3）最后用误分个数占样本总数比率作为随机森林的oob误分率。

随机森林RF调参

决定补一下sklearn中随机森林的参数介绍，和调参。

classsklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)

1. 指标参数criterion:

Criterion用来决定结点不纯度计算方法，sklearn提供两种选择：
（1）entropy: 信息熵Entropy；
（2）gini: 基尼指数Gini Impurity；
具体计算方法可参照前文。

默认基尼系数；

比起基尼系数, 信息熵对不纯度更加敏感，对不纯度惩罚最强。但实际使用中，两者效果基本相同；

信息熵的计算比基尼系数缓慢一些，因为基尼系数不涉及对数；

因信息熵对不纯度更加敏感，所以信息熵作为指标时，决策树生长会更加 精细，对于高维数据或者噪音多的数据，信息熵容易过拟合，基尼系数这种情况下效果会好些。当然并非绝对。

数据维度大，噪声大时，建议选基尼系数，纬度低，数据比较清晰时，两者没大区别。当决策树拟合程度不够时，可以都试下，不好可换另一个。

2. 随机模式参数 random_state和splitter

random_state: 设置分枝中随机模式的参数，默认None, 高维度时随机性会表现的更明显，低纬度数据，随机性不会显现。随机性便于调参，理解可参照此篇。

splitter: 用来控制决策树中随机选项，有两种输入值：
（1）best: 决策树在分枝时虽然随机，但还是会优先选择更重要的特征进行分枝；
（2）random: 决策树分枝时更加随机，树会因为含有更多的不必要信息而更深更大，并因这些不必要信息降低对训练集的拟合，但另一个角度来看，也可以防止过拟合。

3. 剪枝参数：

为了让决策树有更好泛化性，对其剪枝。剪枝策略对决策树影响巨大，正确的剪枝策略是优化决策树算法的核心。

（1）max_depth: 限制树的最大深度，超过设定深度的树枝全部剪掉；这是用的最广泛的剪枝参数，高维度低样本量时非常有效。

决策树多生长一层，对样本量的计算需求会增加一倍，所以限制树深度可有效限制过拟合。集成算法中非常实用。

实际实用时，建议从3开始尝试，看看拟合效果决定是否增加。

（2）min_samples_leaf: 一个节点在分枝后的每个子节点必须包含至少min_samples_leaf个训练样本，否则不会分枝。

一般搭配max_depth使用，在回归树中有比较神奇的效果，可以让模型变的更加平滑。

一般，建议从5开始使用。如果叶节点中含有的样本量变化很大，建议输入浮点数作为样本量的百分比来使用。

同时，这个参数可以保证每个叶子的最小尺寸，可以在回归问题上避免低方差，过拟合的叶节点出现。

对于类别不多的分类问题，1通常是最佳选择。

（3）min_samples_split: 一个节点，必须要包含至少min_samples_split个训练样本，才会被允许分枝，否则不会分枝

（4）max_features: 划分时考虑的最大特征数，可以使用多种类型值。

默认None, 意味着划分时考虑所有特征；
$log2$, 划分时，最多考虑$lo{g}_{2}N$个特征；
sqrt/auto, 最多考虑$\sqrt{N}$ 个特征；
整数，考虑的绝对特征数；
浮点数，考虑特征百分比，取整后特征数。

一般来说，特征数不多，如小于50， 默认None, 如果非常多，灵活使用其他取值控制。

（5）min_impurity_decrease: 限制信息增益的大小，小于设定数值时，分枝不会发生。

4. 目标权重参数

（1）class_weitht: 类别权重，主要是为了防止训练集某些类别的样本过多，导致训练的决策树过于偏向这些类别。可以自己指定各个样本的权重，或者用‘balanced’ , 如果使用balanced, 算法会自己计算权重，样本少的类别对应的样本权重会搞，当然，如果样本类别没有明显偏倚，可以不管，默认None。

（2）min_weight_fraction_leaf: 限制了叶子结点所有样本权重和的最小值，如果小于这个值，会和兄弟结点一起被剪枝，默认是0，不考虑权重。一般如果有较多样本有缺失值，或分类树样本分布类别偏差很大，会引入样本权重。

5. 重要属性和接口：

（1）feature_importances_: 能够查看各个特征对模型的重要性；

（2）fit/score: 与其他sklearn类似

（3）apply/predict

参考链接:
RF主页；
RF不错的博文1；
RF不错的博文2；
RF参数详解官方
RF重要参数-简书
sklearn 决策树参数使用

—未完待续—