算法与数据结构----动态规划专题

算法与数据结构----动态规划专题

一、基础概念

1.1 什么是算法？

《算法导论》 ：算法是任何良定义的计算过程，该过程取某个值的集合作为输入并产生某个值或值的集合作为输出。这样算法就是把输入转换成输出的计算步骤的一个序列。
百度百科 ：算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。
维基百科 ：算法（Algorithm），在数学和计算机科学之中，指一个被定义好的、计算机可施行其指示的有限步骤或次序，常用于计算、数据处理和自动推理。算法是有效方法，包含一系列定义清晰的指令，并可于有限的时间及空间内清楚的表述出来。
个人理解 ：算法不是空中阁楼的技巧，而是一系列的可以解决问题的方案，能从具体业务中抽离出来。算法的意义在于更快更好地解决问题，快和准是第二属性，解决问题才是第一属性。下图所示就是一个简单的让电灯工作的算法，简单且有效。

为什么需要算法？ 引用 Linux 内核核心开发者 Robert Love 在 Quora 上的回答：“数据结构与算法的良好基础不是对每个数据结构都知道细节怎么实现，都背下来大 O 复杂度和摊销复杂度，当然知道这些非常好，只是你在工作中很少用到它们，你的职业生涯里几乎不可能让你实现一个红黑树和节点删除算法。但是，你必须知道什么时候 BST(二叉排序树)对于一个问题是个有效的解法”，因此，学习算法的目的，是能够在遇到问题时，选择有效的解决方案。

1.2 经典算法有哪些？

1. 排序算法： 排序算法最经典的莫过于八大排序算法了，分别是：插入排序、冒泡排序、选择排序、希尔排序、堆排序、归并排序、快速排序、桶式排序。
2. 搜索算法： 搜索算法是利用计算机的高性能来有目的的穷举一个问题的解空间的部分或所有的可能情况，从而求出问题解的一种方法。现阶段常用的搜索算法有：枚举算法、深度优先搜索、广度优先搜索、剪枝算法、回溯算法等。
3. 经典算法： 包括分治法，动态规划，贪心策略，回溯等
4. 图算法： Dijkstra算法，求单源最短路径的算法。即求网络中某个特定点v到网络中其他所有节点的最短路径。
   Floyd算法，求网络中任意两点间最短路径的算法。
   Prim算法，求连通图中最小生成树的算法。
5. 树算法： 深度优先遍历和广度优先遍历等。

1.3 算法的复杂度是什么？

1.3.1算法的复杂度

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。
时间效率被称为时间复杂度，而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间，在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
时间复杂度的符号：Ο是渐进上界，Ω是渐进下界。Θ需同时满足大Ο和Ω，故称为确界（必须同时符合上界和下界）。Ο极其有用，因为它表示了最差性能。算法的时间度量记作 $T(n)=O(f(n))$ 。

1.3.2 时间复杂度的计算

计算时间复杂度主要有三种方法：替代法、递归树、主方法。现在有这样一个Java的归并排序代码：

    public static void mergeSort(int[] a, int low, int high) {
        int mid = (low + high) / 2;
        if (low < high) {
            // 左边
            mergeSort(a, low, mid);
            // 右边
            mergeSort(a, mid + 1, high);
            // 左右归并
            merge(a, low, mid, high);
        }

无需考虑merge方法的具体实现，但是能知道merge方法是合并两个有序数组，时间复杂度为Θ(n)。于是可以写出时间复杂度的公式为：
$$T(n)=2T(n/2)+cn,c>0且为常数$$

• 递归树方法
  依据公式构建递归树的结构为：

• 主方法： 主方法适用于此类的递归形式
  $$T(n)=aT(n/b)+f(n),a>1,b>1,f为正渐进函数$$
  主方法有三种情况:
  

归并排序属于情况(2), $f(n)=O(n^{lo{g}_2^2})=O(n)$ 则归并排序时间复杂度为：
$$T(n)=\Theta (nlogn)$$

• 替代法： 替代法是最通用的方法：1.猜测解的形式 2. 通过推导验证 3.解出常数。

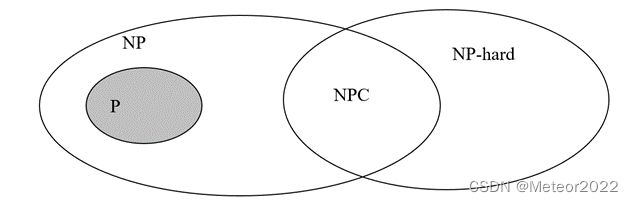
1.3.3 什么是P, NP, NPC, NP-Hard？

P问题： 多项式时间内可解的问题（判定/接受），如排序问题就是一个典型的P类问题。
NP问题： 多项式时间内可验证的问题
NP-hard问题： 任意NP问题都可以在多项式时间内归约为该问题，但该问题本身不一定是NP问题。归约的意思是为了解决问题A，先将问题A归约为另一个问题B，解决问题B同时也间接解决了问题A。例如：旅行家推销问题(TSP)，给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。
NPC问题： 既是NP问题，也是NP-hard问题。例如：哈密顿回路，由指定的起点前往指定的终点，途中经过所有其他节点且只经过一次。 简化来说需要满足两个条件：

1. 是一个NP问题；
2. 所有的NP问题都可以归约到它。

P=NP? 就是若问题的答案可以很快验证，其答案是否也可以很快被计算出来。

1.4 动态规划是什么？

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。 动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。 通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

二、动态规划详解

2.1 简单的动态规划问题

2.1.1 爬楼梯问题

问题： 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。
你有多少种不同的方法可以爬到楼顶呢？

示例 ：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

递归方案解决爬楼梯问题：

class Solution {
    public int climbStairs(int n) {
        // 当n=1或n=2时直接返回
        if(n == 1){
             return 1;
         }
         if(n == 2){
             return 2;
         }
         // 其他情况下，每个台阶都存在上1个和上2个的情况
         return climbStairs(n - 1) + climbStairs(n - 2);
    }
}

存在的问题
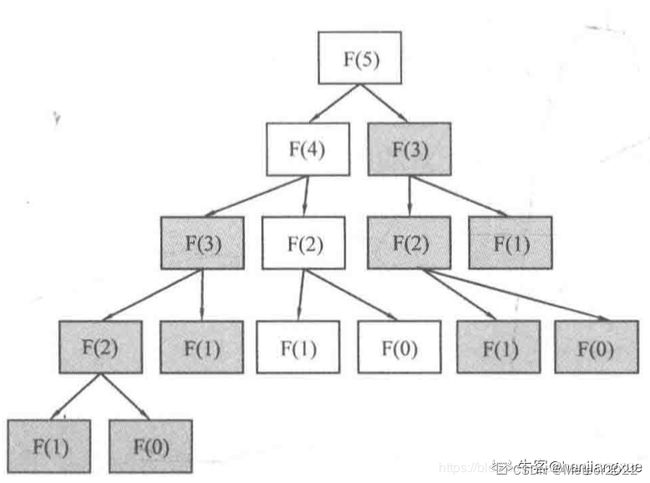
运行结果表面，运行时间超出范围，因此必须优化算法解决这个问题，出现问题的原因是因为在递归计算时，重复多次计算子问题，climbStairs(8) = climbStairs(7)+climbStairs(6)，climbStairs(7) = climbStairs(6)+climbStairs(5)，这种重复计算是浪费性能的，利用递归树的计算方式，可以得出时间复杂度最好的情况为为$\Omega ((logn)\ast 2^{n/2})$，是一个指数级的时间复杂度。

2.1.2 动态规划解决爬楼梯

解决思路： 用 $f(x)$ 表示爬到第 $x$级台阶的方案数，考虑最后一步可能跨了一级台阶，也可能跨了两级台阶，所以可以列出如下动态转移方程：
$$f(x)=f(x-1)+f(x-2)$$
它意味着爬到第 $x$级台阶的方案数是爬到第 $x-1$ 级台阶的方案数和爬到第 $x-2$ 级台阶的方案数的和。很好理解，因为每次只能爬 1 级或 2级，所以$f(x)$ 只能从$f(x-1)$ 和 $f(x-2)$转移过来，而这里要统计方案总数，就需要对这两项的贡献求和。
求解边界条件： 由于是从第0 级开始爬的，所以从第0级爬到第0级我们可以看作只有一种方案，即$f(0)=1$；从第 0 级到第 1级也只有一种方案，即爬一级，$f(1)=1$。
由转移方程和边界条件，能够给出一个时间复杂度和空间复杂度都是 O(n) 的动态规划算法实现

class Solution {
    public int climbStairs(int n) {
        int[] num = new int[n+1];
        // 初始化num, num[i]表示第i级楼梯有num[i]种走法
        num[0] = 1;
        num[1] = 1;
        for (int i = 2; i <= n; ++i) {
            num[i] = num[i-1] + num[i-2];
        }
        return num[n];
    }
}

2.1.3动态规划的基本构成

动态规划用于解决多阶段决策最优化问题，但也不是所有最优化问题都可以用动态规划来解答。动态规划能够解决的问题特征有如下：

1. 最优子结构： 作为整个过程的最优策略具有这样的性质：无论过去的状态和决策如何，相对于前面的决策所形成的状态而言，余下的决策序列必然构成最优子策略。即，一个最优策略的子策略也是最优的。
2. 重叠子问题： 动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，因而不会在解决同样的问题时花费时间。
3. 无后效性： 如果某阶段状态给定后，则在这个阶段以后过程的发展不受这个阶段以前各段状态的影响。

利用上台阶问题解释上述概念，假设台阶数$n=10$；
我们已知$F(10)=F(9)+F(8)$，因此$F(9)$和$F(8)$是$F(10)$的最优子结构，同时上台阶问题存在大量的重叠子问题，比如在需要反复求解$F(3)$的结果，因此满足动态规划的基本要求。同时$F(3)$的结果是唯一的，不会因为后续的计算而影响，因此无后效性。

状态转移方程和边界条件： 动态规划最核心在于如何构建状态转移方程和确定边界条件，上台阶的问题容易理解，并且很容易证明状态转移方程如下：$$F(x)=F(x-1)+F(x-2)$$
同时上台阶问题的边界条件是$F(1)$和$F(2)$时的上台阶方式的数量。但是复杂的动态规划问题难以快速构建状态转移方程和识别边界条件。

2.2 复杂的动态规划问题(多维动态规划)

2.2.1 最长公共子序列

对于一般性的最长公共子序列（longest common subsequence，LCS）问题（即任意数量的序列）是属于NP-hard。但当序列的数量确定时，问题可以使用动态规划在多项式时间内解决。
题目：

给定两个字符串 text1 和 text2，返回这两个字符串对应的最长公共子序列的长度。如果不存在公共子序列，返回 0 。
一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

例子：

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3。

动态规划思路： 首先找出状态转移方程，题中求最长公共子序列的长度。
因此计LCS(i,j)记为两个字符串中x[0,...,i]与y[0,...,j]的最大公共子序列的长度，利用c[i,j]表示。那么如果x[i]==y[j]则c[i][j]=c[i-1][j-1] + 1而如果x[i]!=y[j]则c[i][j]=max(c[i][j-1],c[i-1][j])。即最优子结构。对于c[i][j]会在计算c[i+1][j],c[i][j+1],c[i+1][j+1] 时重复使用，存在重复子问题，并且后续计算结果对c[i][j]无后效性，满足使用动态规划的条件。
边界问题： 当i=0或者j=0时，必定有个子串长度为0，因此c[i,0]=c[0,j]=0。
如上述例子当i=1且j=1时，c[1][1] = 0+1=1，即字符串text1中的子序列’a’和字符串text2中的子序列’a’最大子序列长度为1。当i=2且j=2时，c[2][2] = max(c[2][1],c[1][2])=max(1,1)=1，即即字符串text1中的子序列’ab’和字符串text2中的子序列’ac’最大子序列长度为1，归纳出状态转移方程为：

证明状态转移方程成立：

1. 当x[i]=y[j]时，令 z[0,...,k]=LCS(x[0,...,i], y[0,...,j])，此时 c[i,j]=k+1。
2. 如果z[k]≠x[i]，那么,可以扩增 z(矛盾) ；或者z[k] = x[i]，这样（只需证）z[0,...,k-1]是x[0,...,i-1] 和 y[0,...,j-1]的 LCS。
3. 需证明z[0,...,k-1] = LCS(x[0,...,i-1], y[0,...,j-1])。假设w是x[0,...,i-1]和y[0,...,j-1]一个更长的 LCS ，即 |w| > k–1。
4. 那么，存在 (w||z[k]) (w与z[k] 连接) 是x[0,...,i] 和 y[0,...,j]的公共子序列，同时|w||z[k]| > k。自相矛盾，由此声明得证。
5. 这样, c[i–1, j–1] = k–1, 意味着c[i,j]= c[i–1, j–1] + 1.

代码实现：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            char c1 = text1.charAt(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.charAt(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}

复杂度分析
时间复杂度：$O(mn)$，其中 m 和 n 分别是字符串 text1和text2的长度 。二维数组 dp有 m+1行和 n+1列，需要对 dp 中的每个元素进行计算。
空间复杂度：$O(mn)$，其中 m 和 n 分别是字符串 text1和text2的长度 。创建了 m+1 行n+1 列的二维数组 dp。

2.2.2 0-1背包问题

背包问题是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。同时0-1背包也是动态规划中最经典的问题之一。

题目描述：

有 goodsNum 件物品和一个容量是 bagCapacity的背包。每件物品只能使用一次。给定一个数组values代表物品价值，给定一个数组weights代表物品重量。
第 i件物品的体积是 weights[i]，价值是values[i]。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

例子：

输入：weights=[1,2,3,4]，values=[2,4,4,5]，goodsNum=4，bagCapacity=5
输出：8

构建状态转移方程：

1. 状态dp[i][j]定义：前 i 个物品，背包容量 j 下的最优解（最大价值）：当前的状态依赖于之前的状态，可以理解为从初始状态dp[0][0] = 0开始决策，有 N 件物品，则需要 N次决策，每一次对第 i件物品的决策，状态dp[i][j]不断由之前的状态更新而来。
2. 当前背包容量不够（j < w[i]），没得选，因此前i个物品最优解即为前i−1个物品最优解：f[i][j] = f[i - 1][j]。
3. 当前背包容量够，可以选，因此需要决策选与不选第 i 个物品，选：f[i][j] = f[i - 1][j - w[i]] + v[i]，不选：f[i][j] = f[i - 1][j]。我们的决策是如何取到最大价值，因此以上两种情况取 max() 。

实现代码:

class Solution {
    public int maxValueBags(int[] values, int[] weights, int goodsNum, int bagCapacity) {
        int[][] dp = new int[goodsNum + 1][bagCapacity + 1];
        dp[0][0] = 0;
        for (int i = 1; i <= goodsNum; i++) {
            for (int j = 0; j <= bagCapacity; j++) {
                if (j >= weights[i]) {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i]);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[goodsNum][bagCapacity];
    }
}

背包容量计算结果：

价值	1	2	3	4	5
1	2	2	2	2	2
2	2	4	6	6	6
3	2	4	6	6	8
4	2	4	6	6	8

除0-1背包问题外，利用动态规划还可以解决完全背包问题，多重背包问题 ，混合背包问题等问题。

三、动态规划与其他算法比较

3.1 动态规划与贪心策略的差异

动态规划 ,动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。
贪心算法（英语：greedy algorithm），又称贪婪算法，是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。比如在旅行推销员问题中，如果旅行员每次都选择最近的城市，那这就是一种贪心算法。
简单来说： 贪心算法当前决定的一定是最好的，而动态规划是需要根据当前状态进行选择。举例来说，动态规划相当于自助餐，你需要通过的胃口和物品的好吃程度去决定要不要吃，而贪心算法是你肚子一定可以装的下，你每次都可以毫无顾及的选择吃与不吃。

例题：

与0-1背包相似， 有 $N$ 个金子和一个容量是 $V$的背包，但是金子可以切割
第 $i$ 个金子的体积是 $v_i$，价值是$w_i$。
求解将如何将金子装入背包，可使这些金子的总体积不超过背包容量，且总价值最大。

将物品是否可取(0-1背包)变成中物品变成可分的，就变成部分背包问题，部分背包问题可以利用贪心策略解决。实现代码如下：

    class Goods {
        double value;
        double weight;
    }
    public double maxValueBags(Goods[] goods, int goodsNum, double bagCapacity) {
        // 对物品的单价进行排序操作
        Arrays.sort(goods, (x, y) -> Double.compare(y.value / y.weight, x.value / x.weight));
        double resCap = bagCapacity;
        double maxValue = 0;
        // 重复选择单位最大价值的商品
        for (int i = 0; i < goodsNum; ++i) {
            if (goods[i].weight >= resCap) {
                maxValue += goods[i].value;
                resCap -= goods[i].weight;
            } else {
                maxValue += resCap * (goods[i].value / goods[i].weight);
            }
        }
        return maxValue;
    }

3.2 记忆化搜索

3.2.1 记忆化搜索 vs 简单动态规划

记忆化搜索: 记忆化搜索是一种通过记录已经遍历过的状态的信息，从而避免对同一状态重复遍历的搜索实现方式。因为记忆化搜索确保了每个状态只访问一次，它也是一种常见的动态规划实现方式。日常所说的动态规划主要指递推。
相同点： 都有重叠子问题，且相比暴力求解，使用这两种方法进行优化的目的是要跳过这些重叠子问题；都有 边界条件和状态转移方程。
区别主要有五点：

1. 记忆化搜索是递归，而动态规划是递推。一般来说，在相同计算量下，因为需要不断调用函数，递归的开销要比递推更大；
2. 记忆化搜索是自顶向下求解，从目标状态到边界条件；而狭义动态规划是自底向上，从边界条件到目标状态；
3. 记忆化搜索不需要严格设计好计算顺序，没有记录则进行计算即可；而动态规划必须分析已有的结果，严格设计 递推计算顺序；
4. 记忆化搜索是以使用记忆化方式避免重复计算来跳过重叠子问题的，而动态规划是以设计巧妙的递推顺序来压根就不产生重叠子问题的。
5. 多个状态下，动态规划通常会生成大量无效的状态，而记忆化搜索则不会，这是记忆化搜索在速度上有可能超越狭义动态规划的地方。

3.2.2 记忆化搜索解决上台阶问题

    //使用数组/集合记录已经计算出来的数，减少重复计算的时间
     HashMap<Integer, Integer> map = new HashMap<>();
     public int climbStairs1(int n) {
         if(n == 1){
             return 1;
         }
         if(n == 2){
             return 2;
         } 
         if(map.get(n) != null){
             return map.get(n);
         } else{
             int result = climbStairs(n - 1) + climbStairs(n - 2);
             map.put(n, result);
             return result;
         }
     }

四、总结

动态规划与其说是一个算法，不如说是一种方法论。该方法论主要致力于将合适的问题拆分成三个子目标：

1. 建立状态转移方程
2. 缓存并复用以往结果
3. 按照一定的顺序计算结果

通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。它的主要思想就是：若要解一个给定问题，我们需要解其不同部分（即子问题），再合并子问题的解以得出原问题的解。 通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量： 一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。通俗来说就是：大事化小，小事化无。